无约束优化——线性搜索法
无约束优化——线性搜索法(line search)
-
- 前言
- 概述
- 构建关于步长的函数
- Wolfe条件
- Strong Wolfe条件
- Zoutendijk条件
- 后记
前言
该系列为学习笔记系列,所有内容可以在 Numerical Optimization (2nd Edition) 中找到,该书十分有用经典建议阅读英文原版。该系列只做简单描述。
概述
数值方法即 通过 迭代 的方法得到 误差允许 范围内的(全局or)局部最优解。它的一般形式是 x k + 1 = x k + α k p k x_{k+1}=x_k+\alpha_kp_k xk+1=xk+αkpk,线搜索方法(line search)和信赖域方法(trust region)是两种不同的 搜索策略,并应用于不同的 搜索方法 上,如:最速下降法(Steepest Descent method)、牛顿法(Newton’s method)、拟牛顿法(Quasi-Newton’s method).这两种策略最显而易见的区别是寻找下一个迭代点的 顺序 不同:先搜索方法先确定方向 (direction: α k \alpha_k αk),再确定步长 (step length: p k p_k pk)。而信赖域方法正好相反。
构建关于步长的函数
这个小标题十分直白,使用线搜索方法时,首先根据优化的式子选择合适的 搜索方法,这一步便确定了 搜索方向。也就是说,线搜索策略是选定搜索方法(方向)后的步长确定策略。下面简略列出不同搜索方法的搜索方向:
| 最速下降法 | 牛顿法 | 拟牛顿法 |
|---|---|---|
| - ∇ f k \nabla f_k ∇fk | - ( ∇ 2 f k ) − 1 ∇ f k (\nabla^2f_k)^{-1}\nabla f_k (∇2fk)−1∇fk | - ( B k ) − 1 ∇ f k (B_k)^{-1}\nabla f_k (Bk)−1∇fk |
所以当选定某种方法后 , x k + 1 = x k + α k p k x_{k+1}=x_k+\alpha_kp_k xk+1=xk+αkpk 中的 p k p_k pk 是确定的。我们希望找到一个 α k \alpha_k αk 使得, f ( x k + 1 ) f(x_{k+1}) f(xk+1) 即 f ( x k + α k p k ) f(x_k+\alpha_kp_k) f(xk+αkpk) 尽可能地小。
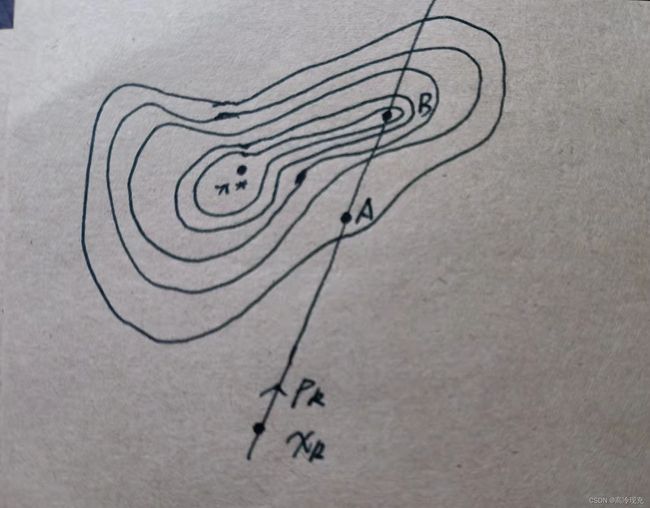
注意:要求 min α k f ( x k + α k p k ) \min_{\alpha_k}f(x_k+\alpha_kp_k) minαkf(xk+αkpk) 是不合理的,一方面,它代价高昂,与其花费巨大代价找到全局最小值,不如一个局部最小值来得实惠,实际上,也没必要要求至少局部最小。另外一方面,即使不计代价找到每一步的全局最小值,它也只是目标函数在该迭代方向上的最小值,放眼全局,该点不一定更靠近目标函数的全局最优点。这里简略手绘说明一下:
( x ∗ x^* x∗为目标函数的最小值点,考虑 x k x_k xk,现在方向确定,要来确定步长,B点是该方向上目标函数的极小值点,但是放眼全局,B点距 x ∗ x^* x∗ 的距离显然要比A大,而且花的代价还比A高)
构建关于步长的函数:
ϕ ( α ) = f ( x k + p k α ) , α > 0 \phi(\alpha)=f(x_k+p_k\alpha),~~\alpha >0 ϕ(α)=f(xk+pkα), α>0
这是一个关于步长的函数,其导数为 ϕ ′ ( α ) = ⟨ ∇ f ( x k + p k α ) , p k ⟩ = ∇ f ( x k + p k α ) T p k \phi'(\alpha)=\langle~\nabla f(x_k+p_k\alpha),p_k\rangle=\nabla f(x_k+p_k\alpha)^Tp_k ϕ′(α)=⟨ ∇f(xk+pkα),pk⟩=∇f(xk+pkα)Tpk
Wolfe条件
先给出式子:
Wolfe { Armijo condition: f ( x k + α p k ) ≤ f ( x k ) + c 1 α ∇ f k T p k c 1 ∈ ( 0 , 1 ) Curvature condition: ∇ f ( x k + α p k ) T p k ≥ c 2 ∇ f k T p k c 2 ∈ ( c 1 , 1 ) \text{Wolfe}\left\{\begin{matrix} \text{Armijo condition:}~f(x_k+\alpha p_k)\le f(x_k)+c_1\alpha\nabla f_k^Tp_k&c_1\in(0,1)\\\\ \text{Curvature condition: }\nabla f(x_k+\alpha p_k)^Tp_k\ge c_2\nabla f_k^Tp_k&c_2\in(c_1,1) \end{matrix} \right. Wolfe⎩ ⎨ ⎧Armijo condition: f(xk+αpk)≤f(xk)+c1α∇fkTpkCurvature condition: ∇f(xk+αpk)Tpk≥c2∇fkTpkc1∈(0,1)c2∈(c1,1)
其中, Armijo条件确保新的迭代点使得目标函数值下降,也就是下图中斜线的下方。考虑Curvature条件,注意到乘积 ∇ f k T p k \nabla f_k^Tp_k ∇fkTpk 是个负值,所以不等式左边要么大于零,要么小于零但比右边更接近于0(越平),这样的条件更有利于我们选取合适的步长。
Strong Wolfe条件
与Wolfe的不同之处在于Curvature条件,形式如下:
Strong Wolfe { Armijo: f ( x k + α p k ) ≤ f ( x k ) + c 1 α ∇ f k T p k c 1 ∈ ( 0 , 1 ) Curvature: ∣ ∇ f ( x k + α p k ) T p k ∣ ≤ ∣ c 2 ∇ f k T p k ∣ c 2 ∈ ( c 1 , 1 ) \text{Strong Wolfe}\left\{\begin{matrix} \text{Armijo:}~f(x_k+\alpha p_k)\le f(x_k)+c_1\alpha\nabla f_k^Tp_k&c_1\in(0,1)\\\\ \text{Curvature: }|\nabla f(x_k+\alpha p_k)^Tp_k|\le |c_2\nabla f_k^Tp_k|&c_2\in(c_1,1) \end{matrix} \right. Strong Wolfe⎩ ⎨ ⎧Armijo: f(xk+αpk)≤f(xk)+c1α∇fkTpkCurvature: ∣∇f(xk+αpk)Tpk∣≤∣c2∇fkTpk∣c1∈(0,1)c2∈(c1,1)
我们刚刚提到Wolfe中curvature条件的意义为:选取斜率为正或者是虽然为负,但比 c 2 ∇ f k T p k c_2\nabla f_k^Tp_k c2∇fkTpk 更平坦的点。我们其实很容易发现它的缺陷:就是对于斜率为正的情况,我们没有进行约束,如果我们让正斜率没那么大是不是会更好呢?
也就是说,无论斜率是正还是负,它都 足够平坦
此外还有Goldstein条件,此处不再赘述。截取原书的话:
Wolfe: particularly important in the implementation of Quasi-Newton methods
Goldstein: are often used in Newton-type methods, not well suited in Quasi-Newton
Zoutendijk条件
这个是非常重要的东西,学习时务必重视,它的身影时常出现在各种分析算法收敛速度,充分性之中。虽是笔记,但还是想把这段的原文放一下:
It quantifies the effect of properly chosen step lengths α_k , and shows, for example, that the steepest descent method is globally convergent. For other algorithms, it describes how far pk can deviate from the steepest descent direction and still produce a globally convergent iteration. Various line search termination conditions can be used to establish this result, but for concreteness we will consider only theWolfe conditions (3.6). Though Zoutendijk’s result appears at first
to be technical and obscure, its power will soon become evident.
定义一个算法,需看该算法是否满足 有限步性,Zoutendijk条件正是这一问题的充分条件。简单来讲,我们希望迭代步一方面不会走得很慢,基本在原地打转,另一方面,我们希望它不会一直走一直走,走了无穷远的路。这也是研究次梯度算法(subgradient algorithm)时的关键一环。
∑ k ≥ 0 cos 2 θ k ∥ ∇ f k ∥ 2 < ∞ \sum_{k\ge 0}\cos^2\theta_k\| \nabla f_k\|^2<\infty k≥0∑cos2θk∥∇fk∥2<∞
我并不打算把重点放在式子的形式上,我更视 Zoutendijk 条件为一种顺其自然的想法。像是我去某个地方,有时间阶段地行进,那我肯定会想:这一步一步地,究竟能不能到目的地啊?要是到不了,我就不走了。
下一个问题,什么情况下符合这种条件?书中用到了 Lipschitz 条件,即存在一个正的常数 L > 0 L>0 L>0 使得,
∥ ∇ f ( x 1 ) − ∇ f ( x 2 ) ∥ ≤ L ∥ x 1 − x 2 ∥ , ∀ x 1 , x 2 \|\nabla f(x_1)-\nabla f(x_2)\|\le L\|x_1-x_2\|,~~\forall x_1,x_2 ∥∇f(x1)−∇f(x2)∥≤L∥x1−x2∥, ∀x1,x2
题外话,在次梯度算法中,则利用了投影的非扩张性(Nonexpansiveness of the Projection)
后记
原文内容非常多,且该系列需要一定数学基础,我只记录想法。