Windows平台软件工程关键路径PDM图

我是荔园微风，作为一名在IT界整整25年的老兵，今天来聊聊Windows平台下软件工程实践中涉及关键路径问题时常用的PDM图。

PDM图

我们用工程实例来完整讲解PDM图的节点表示， ES(最早开始时间) 、 LS(最迟开始时间)、EF(最早完成时间)、LF(最迟完成时间)推导，以及关键路径的推导。

项目描述

某系统集成项目的建设方要求必须按合同规定的期限交付系统，承建方项目经理决定严格执行项目进度管理，以保证项目按期完成。经理决定使用关键路径法来编制项目进度PDM图。 在对工作分解结构进行认真分析后，经理得到了一张包含活动先后关系和每项活动初步历时估计的工作列表，见下。

活动关系及历时列表

活动代号          前序活动         活动历时/天

A                       -                        5

B                       A                       3

C                       A                       6

D                       A                       4

E                       B、C                 8

F                       C、D                 5

G                       D                       6

H                       E、F、G            9

(1)画出该系统集成项目的PDM图。

(2)标记各节点的ES、LS、EF、LF。

(3)求该PDM图关键路径。

PDM图中求各节点的ES、LS、EF、LF及求关键路径的方法一般分为如下6步：

第1步：将工作表转换为PDM图。

我们使用矩形代表活动，活动间使用箭线连接，表示活动之间的逻辑关系。PDM图存在4种依赖关系，目前各论坛中我看到的画的最好的图就是下面这张。

(1)FS(结束一开始)。表示前序活动结束后，后续活动才可以开始。

(2)FF(结束一结束)。表示前序活动结束后，后续活动才可以结束。

(3)SS(开始一开始)。表示前序活动开始后，后续活动才可以开始。

(4)SF(开始一结束)。表示前序活动开始后，后续活动才可以结束。

PDM图中，活动(即节点)的表示图中，目前各论坛中我看到的画的最好的图就是下面这张。

其中，节点中各时间的关系如下：
(1)ES(最早开始时间)+工期=EF(最早完成时间)。
(2)LS(最晚开始时间)+工期=LF(最晚完成时间)。
(3)LS(最晚开始时间)-ES(最早开始时间)=TF(总时差)=LF(最晚完成时间)-EF(最早完成时间)。

将工作列表转换为PDM图，目前各论坛中我看到的画的最好的图就是下面这张。。

确定起点：活动A没有前序活动，因此活动A为起点。
确定终点：活动H没有后续活动，因此活动H为终点。
确定依赖关系：工作列表给出活动B的前序为A,因此在PDM图中，有一条从A到B的射线。
确定工期：工作表给出的活动历时，即为各项活动的工期。

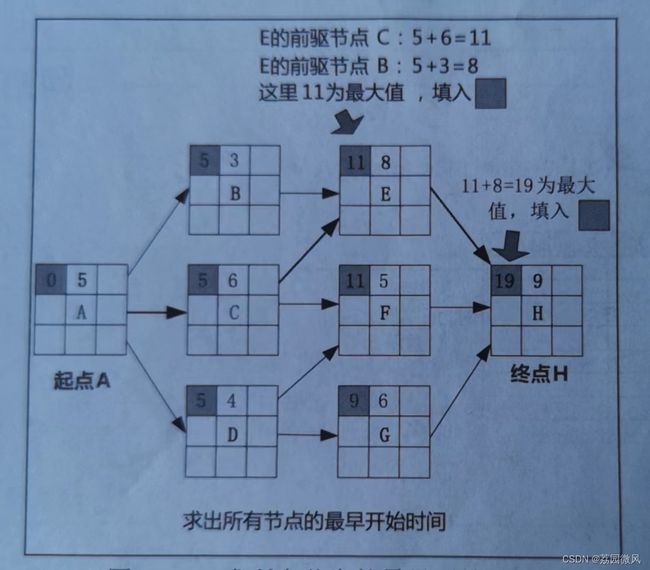
第2步：从左至右求各节点的最早开始时间。

目前各论坛中我看到的画的最好的图就是下面这张，节点B的所有前序节点的MAX{最早开始时间+工期}，即为节点B的最早开始时间(ES)。

 根据如上思路，得到对应PDM图所有节点的最早开始时间，目前各论坛中我看到的画的最好的图就是下面这张：

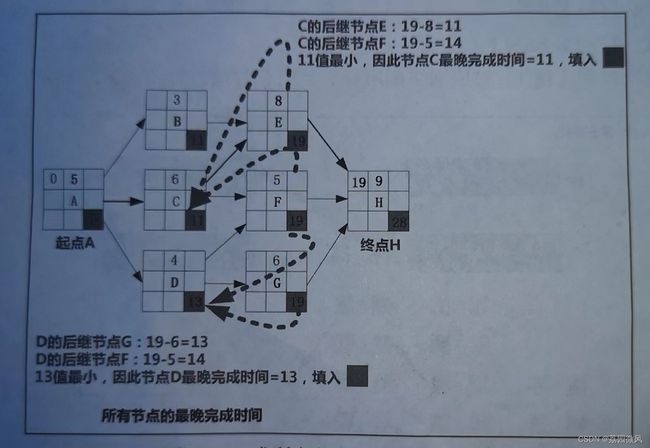
第3步：从右至左求各节点的最晚完成时间。
a.终点H的最晚完成时间等于H的最早开始时间加上H的历时。
b.除H以外的其他节点，其最晚完成时间=MIN后续节点{最晚完成时间-活动历时}，目前各论坛中我看到的画的最好的图就是下面这张。

根据上述逻辑，可得PDM图中所有节点的最晚完成时间，目前各论坛中我看到的画的最好的图就是下面这张。

 第4步：求最早完成时间、最晚开始时间、关键路径。

根据节点的时间关系，求最早完成时间、最晚开始时间、时间差。其中，ES=LS或者EF=LF的节点均可视为关键路径节点。尝试连接这些节点，能从起点连接到终点的，就是关键路径。

根据上述逻辑，可得到题目对应PDM图所有节点的最早完成时间、最晚开始时间、关键路径，目前各论坛中我看到的画的最好的图就是下面这张。

第5步：求总时差。

某个节点的总时差是指其在不影响总工期的前提下所具有的机动时间。每个活动总时差（机动时间)用完后，必须马上开始，否则将会耽误工期。关键路径上的节点总时差为0。

总时差公式：TF=LS-ES=LF-EF。

根据上述逻辑得到对应PDM图所有节点的总时差，目前各论坛中我看到的画的最好的图就是下面这张。

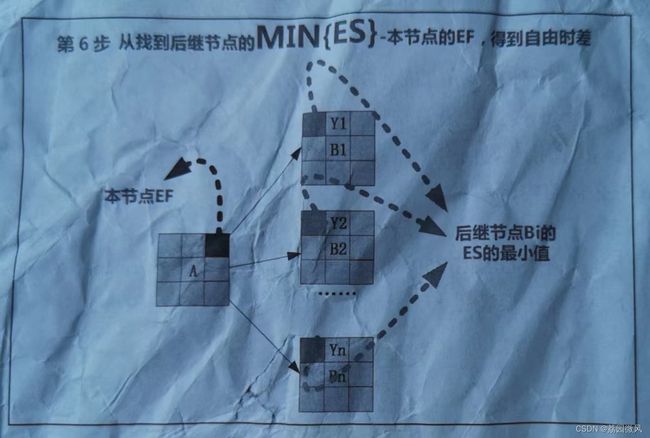
第6步：求自由时差。
自由时差是指不影响后继节点最早开始时间的前提下的本节点的机动时间。如图所示，节点A的所有后继节点的MIN{ES}-本节点的EF， 即为节点A的自由时差。

大家要尽快熟练这个方法，不然在实践中很容易用不起来。

作者简介：荔园微风，1981年生，高级工程师，浙大工学硕士，软件工程项目主管，做过程序员、软件设计师、系统架构师，早期的Windows程序员，Visual Studio忠实用户，C/C++使用者，是一位在计算机界学习、拼搏、奋斗了25年的老将，经历了UNIX时代、桌面WIN32时代、Web应用时代、云计算时代、手机安卓时代、大数据时代、ICT时代、AI深度学习时代、智能机器时代，我不知道未来还会有什么时代，只记得这一路走来，充满着艰辛与收获，愿同大家一起走下去，充满希望的走下去。