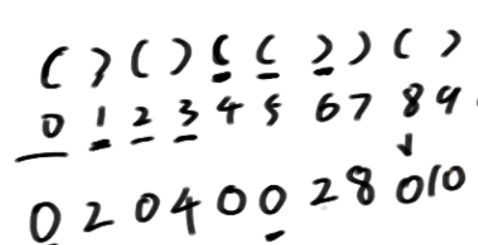每天几道高频算法题-DAY1
从今天开始 每天做几道高频算法题 备战秋招 如果有算法还没刷题的(买不起LeetCode会员的) 可以和我一起刷
题目一
给定一个有序数组arr,从左到右依次表示X轴上从左往右点的位置,给定一个正整数K,返回如果有一根长度为K的绳子,最多能盖住几个点绳子的边缘点碰到X轴上的点,也算盖住
思路1:
最暴力解的话就是把绳子的开头 放在每一个点上 然后遍历出结果之后选一个最大值 这样的话时间复杂度会达到O(N)
思路2:
这个方法是使用了滑动窗口法的变种,维护一个数组作为窗口,先以arr[0]为窗口的头部
然后判断窗口最多能拓展到哪个节点 然后窗口左侧滑动一个单位(就是以arr[1]开头了 本质上是窗口头部向右走了一个元素),然后再看窗口最远可以包含住哪个节点,用max抓住以每个数为开头的最大节点;
public static int MaxPoint(int K,int [] arr) {
int left = 0;
int right = 1;
int max = Integer.MIN_VALUE;
while(left
题目二
括号有效配对是指:
1)任何一个左括号都能找到和其正确配对的右括号
2)任何一个右括号都能找到和其正确配对的左括号
有效的: (())()()(()())等
无效的:(())(等
问题一:怎么判断一个括号字符串有效?
问题二:如果一个括号字符串无效,返回至少填几个字符能让其整体有效
问题三:返回一个括号字符串中,最长的括号有效长度() 红色困难
问题一
很简单问题1 无论是单调栈法 还是遍历法都可以 这里只做最优解
我们定一个整形 初始为0 遍历字符串遇到一个左括号加1遇到一个右括号减1 但是如果它变成负数了 直接跳出循环 返回为假
对于左括号来说 只要右边有和它配对的右括号 就算有效
但是对于右括号来说 如果它的左边没有和它配对的左括号 那后面有一万个左括号也不好使了
public static boolean Islegal(String string) {
int count = 0;
char [] chars = string.toCharArray();
for (char c : chars) {
if(c=='(') {
count++;
}
else if(c==')') {
count--;
}
if(count<0) {
return false;
}
}
if(count==0) {
return true;
}
return false;
}问题二
public static int Islegal(String string) {
int count = 0;
int result = 0;
char [] chars = string.toCharArray();
for (char c : chars) {
if(c=='(') {
count++;
}
else if(c==')') {
count--;
}
if(count<0) {
result++;
count = 0;
}
}
result += count;
return result;
}和问题一大概流程一致 需要注意的点是 当count<0的时候表示现在有一个)没有匹配 所以我们要立刻把result加一 因为如果不处理的话 后面会有一个左括号加上 然后result变成0 这很显然是逻辑不通的 例:)( 这样虽然result为0 但实际上并不合规
问题三
最暴力的解法是遍历以每一个字符结尾(或开头)的字符串 然后找出最大值,经典O(N²)复杂度
有只遍历字符串一遍的做法
创建一个与字符数组等长的数组 每个数组的元素放 以当前位置结尾的最长有效字符串
仅仅是这样的话似乎和全遍历没啥区别 优化在于
1.以左括号结尾的字符串 以当前位置结尾的最长有效字符串长度肯定为0(此后用'值'来表示)
2.以右括号结尾的字符串的值,假设当前位置为M位 看它前一位 假如说 前一位的值为N 那么就看往前推N位的情况(M-N-1位)
如果M-N-1位是左括号 说明有效 那么当前位置的值 就是N的值+2 然后再往前看一位M-N位的值把它也加上
如果M-N+1位是右括号 很遗憾 当前位置的值为0
public int longestValidParentheses(String s) {
if(s==null||s.length()<2){
return 0;
}
char [] chars = s.toCharArray();
int [] arr = new int [chars.length];
arr[0] = 0;
int max = 0;
for(int i = 1;i=0&&chars[t]=='(') {
arr[i] = arr[i-1]+2+(t>0?arr[t-1]:0);
}
}
max = Math.max(max, arr[i]);
}
return max;
} 力扣链接 原题在这里
第三题
有一些排成一 行的正方形。每个正方形已经被染成红色或者绿色。现在可以选择任意一个正方形然后用这两种颜色的任意一种进行染色,这个正方形的颜色将会被覆盖,目标是在完成染色之后,每个红色R都比每个绿色G距离最左侧近。返回最少需要涂染几个正方形。如样例所示:s= RGRGR我们涂染之后变成RRRG满足要求了涂染的个数为2,没有比这个更好的涂染方案
这里的每个红色R比绿色G距离左侧近 说人话就是 所有的红色都应该在绿色的左边
最暴力的解法是 我们遍历每两个格子之间的分界线(包括第一个格子前和 最后一个格子后)
然后把分界线前面全涂成红色 分界线后面全涂成绿色 复杂度是O(N²)
优化解法就是 先过一遍字符串 然后做一个预处理数组 某位置 左侧有多少个G 右侧有多少个R
然后再拿着这个结果 去遍历分界线 就变得简单了
具体实现的话还可以优化一下 先遍历下字符串 看看R总共有多少个 这样从左往右结算的时候 不仅能得出左侧的G有多少个 又能得出右侧的R有多少个 每个位置都计算要涂多少个格子 然后用一个MIN抓住最小的
public static int MinMethod(String string) {
char [] chars = string.toCharArray();
int LeftG = 0;
int RightR = 0;
int RALL = 0 ;
for (char c : chars) {
RALL += c=='R'?1:0;
}
int min = RALL;//对应着把所有的R都涂了 也就是以第一位之前为分界线
RightR = RALL;
for (char c :chars) {
LeftG += (c=='G'?1:0);
RightR -= (c=='R'?1:0);
min = Math.min(LeftG+RightR, min);
}
return min;
}
本来想着今天还能多做几道呢 看了会MYSQL 一抬眼九点了 所以今天就先这样