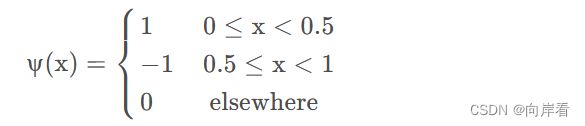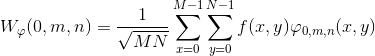图像处理的两种变换：2D-DWT和Gabor变换

 pywt官方API文档： 2D Forward and Inverse Discrete Wavelet Transform 

目录

1. 二维离散小波变换2D-DWT

1.1 二维离散小波变换的相关公式

1.2 使用pywt实现2D-DWT

2.  窗口傅里叶变换Gabor

---

1. 二维离散小波变换2D-DWT

DWT(Discrete Wavelet Transformation)代表离散小波变换。

作用：对于图像来说，它能够将图像变换为一系列的小波系数并将这些系数进行高效的压缩和储存，并且小波的粗略边缘消除了DCT压缩普遍具有的方块效应从而可以更好地还原和表现图像。

 

1.1 二维离散小波变换的相关公式

（1）尺度函数（Father Scaling Function）和小波函数（Mother Wavelet Function）

一种常见的尺度函数，哈尔尺度函数：

一种常见的小波函数，哈尔小波函数：

 

（2） 二维尺度函数和二维小波函数

其中， 是给定的一维尺度函数，是给定的一维小波函数，是一个二维尺度函数，，，分别是沿水平边缘、垂直边缘、对角线方向变化的二维小波函数。

（3） 尺度和平移基函数

 

（4） 二维离散小波变换

 

其中， 是图像的低频子带， ，代表三种不同方向的高频子带，M，H是图像的长和宽，是原图像的离散形式，和是尺度和平移基函数。

（5） 反二维离散小波变换

四种子带图像相加。

1.2 使用pywt实现2D-DWT

（1）pywt.dwt2

作用：进行2D-DWT变换，将原图像分解为四种子带图像。

pywt.dwt2(data, wavelet, mode='symmetric', axes=(-2, -1))

data: 输入的数据
wavelet:小波函数
mode: 默认是对称的

return: (cA, (cH, cV, cD))要注意返回的值，分别为低频分量，水平高频、垂直高频、对角线高频。高频的值包含在一个tuple中。

import numpy as np
from matplotlib import pyplot as plt
import pywt
import PIL

img = PIL.Image.open("1.png")
img = np.array(img)
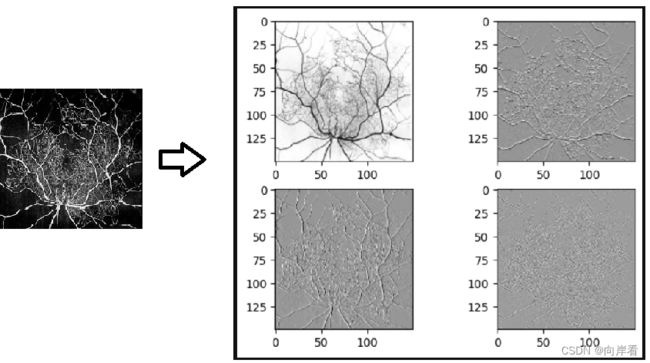
LLY,(LHY,HLY,HHY) = pywt.dwt2(img, 'haar')
plt.subplot(2, 2, 1)
plt.imshow(LLY, cmap="Greys")
plt.subplot(2, 2, 2)
plt.imshow(LHY, cmap="Greys")
plt.subplot(2, 2, 3)
plt.imshow(HLY, cmap="Greys")
plt.subplot(2, 2, 4)
plt.imshow(HHY, cmap="Greys")
plt.show()

 （2） pywt.idwt2

作用：根据分解的四种子带图像，重构原图像。

pywt.idwt2(coeffs, wavelet, mode='symmetric', axes=(-2, -1))

coeffs: 经小波变换后得到的各层的系数
wavelet:小波函数

mode: 默认是对称的

axes：计算DWT的轴

import numpy as np
from matplotlib import pyplot as plt
import pywt
import PIL

img = PIL.Image.open("1.png")
img = np.array(img)
LLY,(LHY,HLY,HHY) = pywt.dwt2(img, 'haar')

# 根据小波系数重构回去的图像
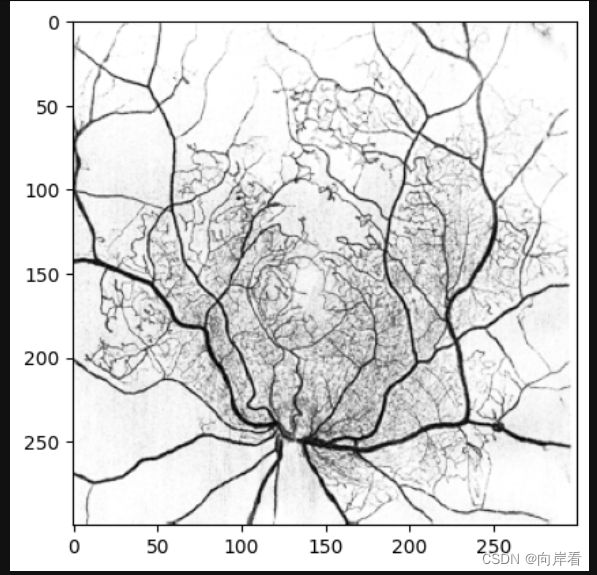
rimg = idwt2((LLY,(LHY,HLY,HHY)), 'haar')

plt.imshow(rimg, cmap="Greys")
plt.show()

重构图像：

 

 

2.  窗口傅里叶变换Gabor

作用：Gabor滤波器可以在频域上不同尺度、不同方向上提取相关的特征。另外，Gabor函数与人眼的作用相仿，所以经常用作纹理识别上，并取得了较好的效果。

（1） skimage.filters.gabor

作用：使用 Gabor 滤波器内核的实部和虚部过滤图像。

skimage.filters.gabor(image, frequency, theta=0, bandwidth=1, sigma_x=None, sigma_y=None, n_stds=3, offset=0, mode='reflect', cval=0) 

参数：

    image：二维阵列，输入图像。
    frequency：浮点数，调和函数的空间频率。以像素为单位指定。
    theta：浮点数，可选，以弧度表示的方向。如果为 0，则谐波在 x 方向。
    bandwidth：浮点数，可选，滤波器捕获的带宽。

    sigma_x, sigma_y：浮点数，可选，x- 和 y-directions 的标准偏差。
    n_stds：标量，可选，内核的线性大小是 n_stds(默认为 3)标准差。
    offset：浮点数，可选，以弧度为单位的谐波函数的相位偏移。
    mode：{‘constant’, ‘nearest’, ‘reflect’, ‘mirror’, ‘wrap’}，可选，用于将图像与内核卷积的模式
    cval：标量，可选，填充过去输入边的值

返回：

    real, imag：数组

（2）取模

skimage.filters.gabor()函数返回的是图像变换后的实部和虚部，在图像识别领域一般使用其模作为图像特征。

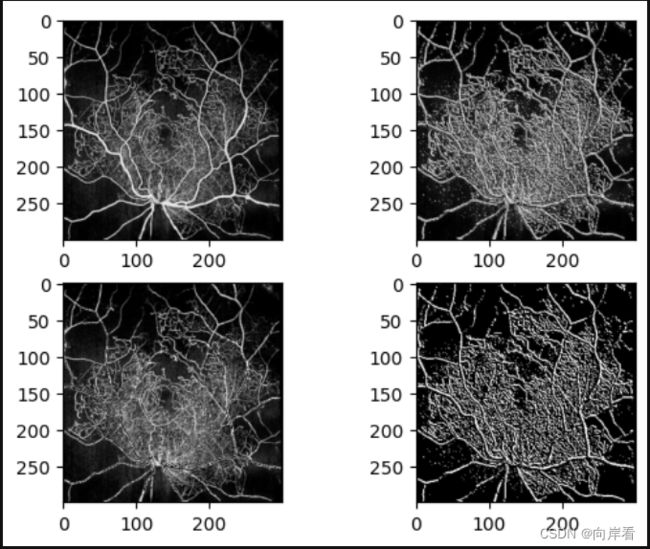
import matplotlib.pyplot as plt
from skimage import filters,io,color
import numpy as np

filename='1.png'
img = io.imread(filename)#读取图像

#调用gabor函数
real, imag = filters.gabor(img, frequency=1.5,theta=45,n_stds=5)
#取模图像
img_mod=np.sqrt(real.astype(float)**2+imag.astype(float)**2)
#图像显示
plt.figure()
plt.subplot(2,2,1)
plt.imshow(img,cmap='gray')
plt.subplot(2,2,2)
plt.imshow(img_mod,cmap='gray')
plt.subplot(2,2,3)
plt.imshow(real,cmap='gray')
plt.subplot(2,2,4)
plt.imshow(imag,cmap='gray')
plt.show()
​

滤波效果：