【动手学深度学习】pytorch-参数管理
pytorch-参数管理
概述
我们的目标是找到使损失函数最小化的模型参数值。 经过训练后,我们将需要使用这些参数来做出未来的预测。 此外,有时我们希望提取参数,以便在其他环境中复用它们, 将模型保存下来,以便它可以在其他软件中执行, 或者为了获得科学的理解而进行检查。
# 创建一个单隐藏层的MLP
import torch
from torch import nn
net = nn.Sequential(nn.Linear(4,8),nn.ReLU(),nn.Linear(8,1))
X = torch.rand(size = (2,4))
net(X)
参数访问
# 参数访问 全连接层包含两个参数 分别是该层的权重和偏置 两者都为存储单精度浮点数
print(net[2].state_dict())
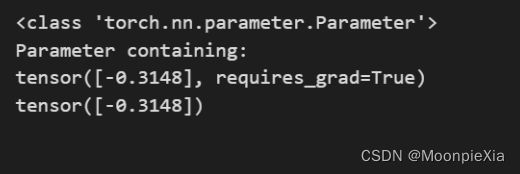
print(type(net[2].bias))
print(net[2].bias)
print(net[2].bias.data)
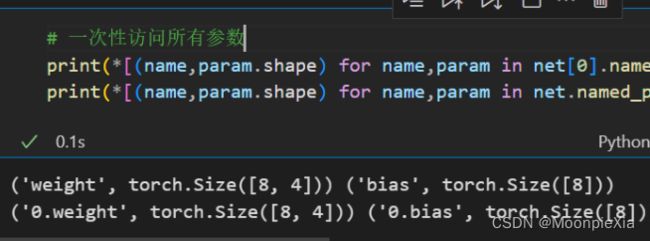
# 一次性访问所有参数
print(*[(name,param.shape) for name,param in net[0].named_parameters()])
print(*[(name,param.shape) for name,param in net.named_parameters()])
嵌套块收集参数
def block1():
return nn.Sequential(nn.Linear(4,8),nn.ReLU(),
nn.Linear(8,4),nn.ReLU())
def block2():
net = nn.Sequential()
for i in range(4):
net.add_module(f'block{i}',block1())
return net
# 块和层之间进行组合
rgnet = nn.Sequential(block2(),nn.Linear(4,1))
rgnet(X)
参数初始化
pytorch根据一个范围均匀初始化权重和偏置矩阵 这个范围是根据输入和输出维度计算得到,Pytorch.init模块提供了多种预置初始化方法。
内置初始化
下面的代码将所有的权重参数初始化为标准差为0.01的高斯随机变量 并且将偏置参数设置为0
def init_normal(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight,mean = 0,std = 0.01)
nn.init.zeros_(m.bias)
net.apply(init_normal)
net[0].weight.data[0],net[0].bias.data[0]
可以将所有的参数初始化为1
def init_constant(m):
if type(m) == nn.Linear:
nn.init.constant_(m.weight,1)
nn.init.zeros_(m.bias)
net.apply(init_constant)
net[0].weight.data[0],net[0].bias.data[0]
针对不同的块进行初始化
def init_xavier(m):
if type(m) == nn.Linear:
nn.init.xavier_uniform_(m.weight)
def init_42(m):
if type(m) == nn.Linear:
nn.init.constant_(m.weight,42)
net[0].apply(init_xavier)
net[2].apply(init_42)
print(net[0].weight.data[0])
print(net[2].weight.data)
自定义初始化
def my_init(m):
if type(m) == nn.Linear:
print("Init", *[(name, param.shape)
for name, param in m.named_parameters()][0])
nn.init.uniform_(m.weight, -10, 10)
m.weight.data *= m.weight.data.abs() >= 5
net.apply(my_init)
net[0].weight[:2]
参数共享
第三层和第四层共享一个参数
shared = nn.Linear(8,8)
net = nn.Sequential(nn.Linear(4,8),nn.ReLU(),
shared,nn.ReLU(),
shared,nn.ReLU(),
nn.Linear(8,1))
net(X)
print(net[2].weight.data[0] == net[4].weight.data[0])