《算法导论》15.5 最优二叉搜索树（含C++代码）

一、问题背景和描述

给定一个n个不同关键字的已排序的序列K=(因此k1 些关键字构造一棵二叉搜索树。对每个关键字k，都有一个概率p，表示其搜索频率。有些要搜
索的值可能不在K中，因此我们还有n+1个“伪关键字"d0，d1，d2, …dn,表示不在K中的值。d₀表示所有小于k的值，d_n 表示所有大于k_n的值，对i=1, 2，…n-1,伪关键字d_i表示所有在k_i和k_i+1之间的值。对每个伪关键字d,也都有一个概率p;表示对应的搜索频率。
图15-9显示了对一个n=5个关键字的集合构造的两棵二叉搜索树。

假定一次搜索的代价等于访问的结点数，即此次搜索找到的结点在T中进行一次搜索的期望代价为：

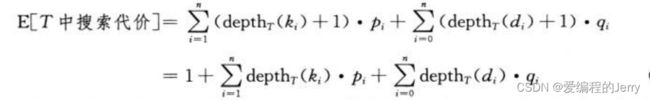
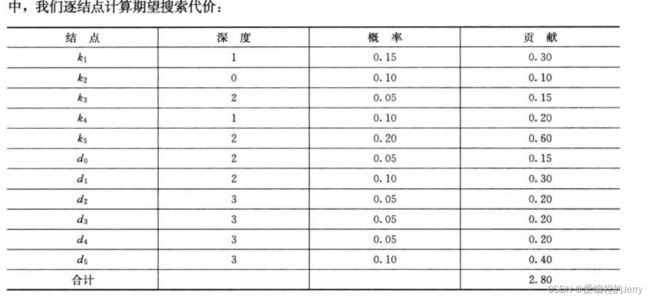
二、解决问题

步骤一：最优二叉搜索树的结构

1、为了刻画最优二叉搜索树的结构，我们从观察子树特征开始。考虑一棵二叉搜索树的任意子
树。它必须包含连续关键字k_i,…,k_j, 1 ≤ i ≤ j ≤ n,而且其叶结点必然是伪关键字d_i-1… d_j。
2、我们现在可以给出二叉搜索树问题的最优子结构：如果一棵最优二叉搜索树T有一棵包含
关键字k_i，…，k_j, 的子树T，那么T必然是包含关键字k_i, …，k_j和伪关键字d_i-1，…，d_j的子问题的最优解。
3、“空子树”：左子树不包含任何关键字，但是包含伪关键字d_i-1，右子树一样，也只包含伪关键字d_j。

步骤二：一个递归算法（挺重要的，直接截图）

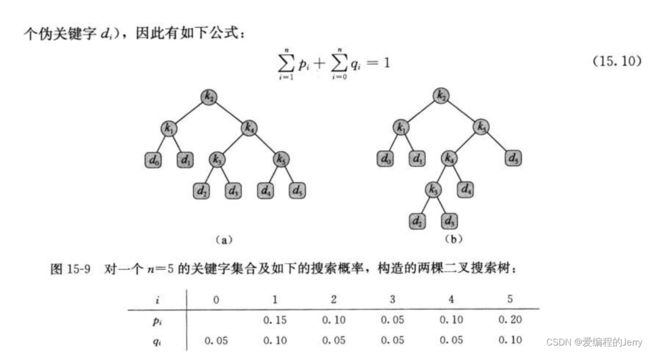
步骤三：计算最优二叉搜索树的期望搜索代价

1、我们用一个表e[1…n+1, 0…n]来保存e[i, j]值。第一维下标上界为n+1而不是n,原因在于对于只包含伪关键字d₀的子树，我们需要计算并保存e[n+1, n]。第二维下标下界为0，是因为对于只包含伪关键字d₀的子树，我们需要计算并保存e[1, 0]。我们只使用表中满足j≥i-1的表项e[i, j]。我们还使用一个表root,表项root[i, j]记录包含关键字k_i,…, k_j的子树的根。我们只使用此表中满足1≤i≤j≤n 的表项root[i, j]。
2、我们还需要另一个表来提高计算效率。为了避免每次计算e[i, j]时都重新计算w(i, j)，我们将这些值保存在表w[1…n+1, 0…n]中，这样每次可节省θ(j-i)次加法。对基本情况，令w[i,i-1] = q_i-1(1≤i≤n+1)。对j≥i的情况，可如下计算:

OPTIMAL-BST(p,q,n)
let e[1...n+1,0...n],w[1...n+1,0...n] and root[1...n,1...n] be new tables
for i = 1 to n+1
	e[i,i-1] = qi-1
	w[i,i-1] = qi-1
for l = 1 to n
	for i = 1 to n-l+1
		j = i+l-1
		e[i,j] = ∞
		w[i,j] = w[i,j-1]+pj+qj
		for r = i to j
			t = e[i,r-1]+e[r+1,j]+w[i,j]
			if(t

C++代码

#include
#include
using namespace std;
void OptimalBinarySearchTree(int n, double* p, double* q, double** root, double** w, double** e);
void printBintree(double** root, int i, int j);

int main()
{
	cout << "最优二叉搜索树 自底向上非递归的动态规划算法\n\n";

	int n;			// 根节点数
	double* p;		// 查找 关键字 的概率
	double* q;		// 查找 虚拟键 的概率
	double** root;	// 根节点
	double** w;		// 子树概率总和
	double** e;		// 子树期望

	cout << "请输入节点数目 n：";
	cin >> n;

	p = new double[n + 1];
	q = new double[n + 1];

	root = new double* [n + 2];
	w = new double* [n + 2];
	e = new double* [n + 2];
	for (int i = 0; i < n + 2; i++)
	{
		root[i] = new double[n + 1];
		w[i] = new double[n + 1];
		e[i] = new double[n + 1];
		//memset(w[i], 0, sizeof(double) * (n + 1));
		//memset(e[i], 0, sizeof(double) * (n + 1));
	}

	cout << "请输入节点查找成功的概率(n个)：";
	for (int i = 1; i <= n; i++)
		cin >> p[i];
	cout << "请输入节点查找失败的概率(n+1个)：";
	for (int i = 0; i <= n; i++)
		cin >> q[i];

	// 构造最优二叉搜索树
	OptimalBinarySearchTree(n, p, q, root, w, e);
	// 输出二叉树
	printBintree(root, 1, n);
	for (int i = 0; i < n + 2; i++)
	{
		for (int j = 0; j < n + 1; j++)
		{
			cout << e[i][j] << "\t";
		}
		cout << endl;
	}
	// 删除指针
	delete[] p;
	delete[] q;
	for (int i = 0; i < n + 2; i++)
	{
		delete[] root[i];
		delete[] w[i];
		delete[] e[i];
	}
	delete[] root;
	delete[] w;
	delete[] e;
}

void OptimalBinarySearchTree(int n, double* p, double* q, double** root, double** w, double** e)
{
	// 处理w[i,j]和e[i,j]中i=j+1的情况，这种情况都是q[i-1]
	for (int i = 1; i <= n + 1; i++) {
		w[i][i - 1] = q[i - 1];
		e[i][i - 1] = 0;
	}
	int i = 0;		// 子问题起始节点的下标
	int j = 0;		// 子问题最后节点的下标
	int r = 0;		// 子问题根节点的下标

	double temp = 0;	// 存放计算得到的临时期望

	// 子问题中节点数量(ki~kj的长度)，从0到n-1
	for (int len = 1; len <= n; len++)
	{
		// 循环所有节点数为len的子问题
		for (i = 1; i <= n - len+1; i++)
		{
			j = len + i-1;
			e[i][j] = INT_MAX;
			w[i][j] = w[i][j - 1] + p[j] + q[j];
			for (r = i ; r <= j; r++)
			{
				temp = e[i][r - 1] + e[r + 1][j] + w[i][j];
				// 保存最优解
				if (temp < e[i][j])
				{
					e[i][j] = temp;
					root[i][j] = r;
				}
			}
		}
	}
}

void printBintree(double** root, int i, int j)
{
	if (i < j)
	{
		int r = root[i][j];
		cout << "S" << r << "是根\n";
		if (root[i][r - 1] > 0)
			cout << "S" << r << "的左孩子是S" << root[i][r - 1] << endl;
		if (root[r + 1][j] > 0)
			cout << "S" << r << "的右孩子是S" << root[r + 1][j] << endl;
		printBintree(root, i, r - 1);
		printBintree(root, r + 1, j);
	}
}