深度学习06-深度卷积生成对抗网络(DCGAN)

概述

GAN（Generative Adversarial Network）是一种生成模型，由两个神经网络组成：生成器（Generator）和判别器（Discriminator）。GAN的基本思想是通过让生成器和判别器相互对抗来学习生成真实样本的能力。

生成器的作用是将一个随机噪声向量作为输入，通过一系列的神经网络层逐渐将其转化为一个与真实样本相似的输出。生成器的目标是尽量使生成的样本被判别器误认为是真实样本，从而欺骗判别器。生成器的训练目标是最小化生成样本与真实样本之间的差异。

判别器的作用是将输入的样本区分为真实样本和生成样本。判别器的目标是尽量准确地判断样本的真伪。判别器的训练目标是最大化判别真实样本和生成样本的能力。

GAN的训练过程可以简述为以下几个步骤：

初始化生成器和判别器的参数。
从真实样本中随机选择一批样本，作为判别器的训练集。同时，生成一批随机噪声向量，作为生成器的输入。
使用生成器生成一批样本，并将其与真实样本混合，构成判别器的训练集。
使用判别器对训练集中的样本进行判别，并计算生成样本与真实样本的损失。
更新生成器和判别器的参数，使生成样本的质量逐渐提高，同时判别器的判别能力也逐渐增强。
重复步骤2-5，直到生成器能够生成与真实样本相似的样本。
DCGAN（Deep Convolutional GAN）是GAN的一种改进版本，主要通过引入卷积神经网络（CNN）来提高生成器和判别器的性能。DCGAN在生成器和判别器中使用了卷积层和反卷积层，使其能够处理图像数据。相较于传统的GAN，DCGAN在生成图像的细节和纹理上有更好的表现。

总的来说，GAN是一种通过生成器和判别器相互对抗来学习生成真实样本的生成模型，而DCGAN是在GAN的基础上引入了卷积神经网络，提高了对图像数据的处理能力。

原理简介

GAN的开山之作是被称为“GAN之父”的Ian Goodfellow发表于2014年的经典论文Generative Adversarial Networks[2]，在这篇论文中他提出了生成对抗网络，并设计了第一个GAN实验——手写数字生成。

GAN的产生来自于一个灵机一动的想法：

“What I cannot create，I do not understand.”（那些我所不能创造的，我也没有真正地理解它。）
—Richard Feynman

类似地，如果深度学习不能创造图片，那么它也没有真正地理解图片。当时深度学习已经开始在各类计算机视觉领域中攻城略地，在几乎所有任务中都取得了突破。但是人们一直对神经网络的黑盒模型表示质疑，于是越来越多的人从可视化的角度探索卷积网络所学习的特征和特征间的组合，而GAN则从生成学习角度展示了神经网络的强大能力。GAN解决了非监督学习中的著名问题：给定一批样本，训练一个系统能够生成类似的新样本。

生成对抗网络的网络结构如图7-2所示，主要包含以下两个子网络。
• 生成器（generator）：输入一个随机噪声，生成一张图片。
• 判别器（discriminator）：判断输入的图片是真图片还是假图片。

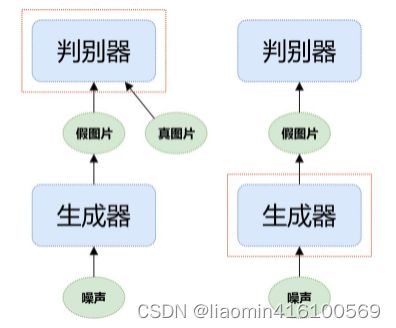
训练判别器时，需要利用生成器生成的假图片和来自真实世界的真图片；训练生成器时，只用噪声生成假图片。判别器用来评估生成的假图片的质量，促使生成器相应地调整参数。

生成器的目标是尽可能地生成以假乱真的图片，让判别器以为这是真的图片；判别器的目标是将生成器生成的图片和真实世界的图片区分开。可以看出这二者的目标相反，在训练过程中互相对抗，这也是它被称为生成对抗网络的原因。
上面的描述可能有点抽象，让我们用收藏齐白石作品（齐白石作品如图7-3所示）的书画收藏家和假画贩子的例子来说明。假画贩子相当于是生成器，他们希望能够模仿大师真迹伪造出以假乱真的假画，骗过收藏家，从而卖出高价；书画收藏家则希望将赝品和真迹区分开，让真迹流传于世，销毁赝品。这里假画贩子和收藏家所交易的画，主要是齐白石画的虾。齐白石画虾可以说是画坛一绝，历来为世人所追捧。

在这个例子中，一开始假画贩子和书画收藏家都是新手，他们对真迹和赝品的概念都很模糊。假画贩子仿造出来的假画几乎都是随机涂鸦，而书画收藏家的鉴定能力很差，有不少赝品被他当成真迹，也有许多真迹被当成赝品。

首先，书画收藏家收集了一大堆市面上的赝品和齐白石大师的真迹，仔细研究对比，初步学习了画中虾的结构，明白画中的生物形状弯曲，并且有一对类似钳子的“螯足”，对于不符合这个条件的假画全部过滤掉。当收藏家用这个标准到市场上进行鉴定时，假画基本无法骗过收藏家，假画贩子损失惨重。但是假画贩子自己仿造的赝品中，还是有一些蒙骗过关，这些蒙骗过关的赝品中都有弯曲的形状，并且有一对类似钳子的“螯足”。于是假画贩子开始修改仿造的手法，在仿造的作品中加入弯曲的形状和一对类似钳子的“螯足”。除了这些特点，其他地方例如颜色、线条都是随机画的。假画贩子制造出的第一版赝品如所示。

当假画贩子把这些画拿到市面上去卖时，很容易就骗过了收藏家，因为画中有一只弯曲的生物，生物前面有一对类似钳子的东西，符合收藏家认定的真迹的标准，所以收藏家就把它当成真迹买回来。随着时间的推移，收藏家买回越来越多的假画，损失惨重，于是他又闭门研究赝品和真迹之间的区别，经过反复比较对比，他发现齐白石画虾的真迹中除了有弯曲的形状，虾的触须蔓长，通身作半透明状，并且画的虾的细节十分丰富，虾的每一节之间均呈白色状。

收藏家学成之后，重新出山，而假画贩子的仿造技法没有提升，所制造出来的赝品被收藏家轻松识破。于是假画贩子也开始尝试不同的画虾手法，大多都是徒劳无功，不过在众多尝试之中，还是有一些赝品骗过了收藏家的眼睛。假画贩子发现这些仿制的赝品触须蔓长，通身作半透明状，并且画的虾的细节十分丰富，如图7-5所示。于是假画贩子开始大量仿造这种画，并拿到市面上销售，许多都成功地骗过了收藏家。

收藏家再度损失惨重，被迫关门研究齐白石的真迹和赝品之间的区别，学习齐白石真迹的特点，提升自己的鉴定能力。就这样，通过收藏家和假画贩子之间的博弈，收藏家从零开始慢慢提升了自己对真迹和赝品的鉴别能力，而假画贩子也不断地提高自己仿造齐白石真迹的水平。收藏家利用假画贩子提供的赝品，作为和真迹的对比，对齐白石画虾真迹有了更好的鉴赏能力；而假画贩子也不断尝试，提升仿造水平，提升仿造假画的质量，即使最后制造出来的仍属于赝品，但是和真迹相比也很接近了。收藏家和假画贩子二者之间互相博弈对抗，同时又不断促使着对方学习进步，达到共同提升的目的。

在这个例子中，假画贩子相当于一个生成器，收藏家相当于一个判别器。一开始生成器和判别器的水平都很差，因为二者都是随机初始化的。训练过程分为两步交替进行，第一步是训练判别器（只修改判别器的参数，固定生成器），目标是把真迹和赝品区分开；第二步是训练生成器（只修改生成器的参数，固定判别器），为的是生成的假画能够被判别器判别为真迹（被收藏家认为是真迹）。这两步交替进行，进而分类器和判别器都达到了一个很高的水平。训练到最后，生成器生成的虾的图片（如图7-6所示）和齐白石的真迹几乎没有差别。

下面我们来思考网络结构的设计。判别器的目标是判断输入的图片是真迹还是赝品，所以可以看成是一个二分类网络，我们可以设计一个简单的卷积网络。生成器的目标是从噪声中生成一张彩色图片，这里我们采用广泛使用的DCGAN（Deep Convolutional Generative Adversarial Networks）结构，即采用全卷积网络，其结构如下图所示。网络的输入是一个100维的噪声，输出是一个3×64×64的图片。这里的输入可以看成是一个100×1×1的图片，通过上卷积慢慢增大为4×4、8×8、16×16、32×32和64×64。上卷积，或称转置卷积，是一种特殊的卷积操作，类似于卷积操作的逆运算。当卷积的stride为2时，输出相比输入会下采样到一半的尺寸；而当上卷积的stride为2时，输出会上采样到输入的两倍尺寸。这种上采样的做法可以理解为图片的信息保存于100个向量之中，神经网络根据这100个向量描述的信息，前几步的上采样先勾勒出轮廓、色调等基础信息，后几步上采样慢慢完善细节。网络越深，细节越详细。

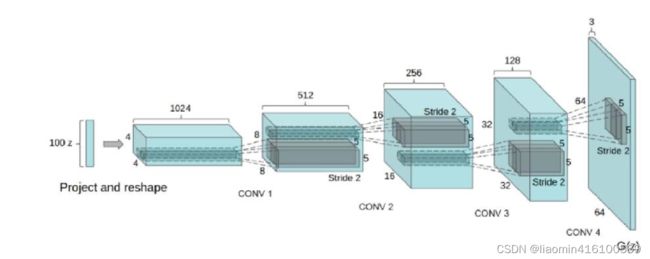
该章节引用自书籍《深度学习框架pytorch，入门到实践》

专业术语

• 上采样(Upsample)在应用在计算机视觉的深度学习领域，由于输入图像通过卷积神经网络(CNN)提取特征后，输出的尺寸往往会变小，而有时我们需要将图像恢复到原来的尺寸以便进行进一步的计算(e.g.:图像的语义分割)，这个采用扩大图像尺寸，实现图像由小分辨率到大分辨率的映射的操作，叫做上采样(Upsample)。
• 矩阵零填充（Zero Padding）是指向矩阵的边界添加零值的过程。在计算机视觉和深度学习中，矩阵零填充常用于图像处理和卷积神经网络（CNN）中。
  在图像处理中，矩阵零填充可以用于扩展图像的尺寸，以便在进行卷积运算时保持图像的大小不变。通过在图像周围添加零值，可以确保卷积核可以完全覆盖图像的边缘像素。这样做可以避免在卷积操作中丢失图像边缘的信息。
  在卷积神经网络（CNN）中，矩阵零填充常用于调整卷积层的输入尺寸和输出尺寸。通过在输入矩阵的边界上添加零值，可以确保卷积操作产生的特征图的尺寸与输入矩阵的尺寸保持一致。这对于构建深度神经网络和处理不同尺寸的输入数据非常重要。
  矩阵零填充的大小通常由填充的行数和列数决定。在CNN中，填充的大小往往与卷积核的大小和步幅相关。通过合理选择填充大小，可以在保持输入输出尺寸一致的同时，控制特征图的尺寸和感受野的大小。
• 反卷积(Transposed Convolution)上采样有3种常见的方法：双线性插值(bilinear)，反卷积(Transposed Convolution)，反池化(Unpooling)，我们这里只讨论反卷积。这里指的反卷积，也叫转置卷积，它并不是正向卷积的完全逆过程，用一句话来解释：反卷积是一种特殊的正向卷积，先按照一定的比例通过补 000 来扩大输入图像的尺寸，接着旋转卷积核，再进行正向卷积。

零填充

对于图像处理中的一些过程，我需要对读取的numpy矩阵进行size的扩充，比如原本是（4，6）的矩阵，现在需要上下左右各扩充3行，且为了不影响数值计算，都用0填充。
比如下图，我有一个4x5大小的全1矩阵，但是现在我要在四周都加上3行的0来扩充大小，最后扩充完还要对原区域进行操作。

1. 如果原始矩阵的形状为 (m, n)，并且在每个边缘上填充了 p 行和 q 列的值，那么填充后的矩阵的形状将是 (m + 2p, n + 2q)
2. 如果原始矩阵的形状为 (m, n)，并且在每个元素之间插入一个零，那么新的矩阵是（m+m-1,n,n-1）=(2m-1,2n-1)

numpy已经封装了一个函数，就是pad

 #%%
import numpy as np
oneArry=np.ones((4,5))
print(oneArry)
print("周围",np.pad(oneArry,3))  #等价于print(np.pad(oneArry,(3,3)))
#注意元组0是左上角补充3行 ，元组1表示右小角
print("左上角",np.pad(oneArry,(3,0)))
print("右下角",np.pad(oneArry,(0,3)))

输出

[[1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1.]]
周围 [[0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 1. 1. 1. 1. 1. 0. 0. 0.]
 [0. 0. 0. 1. 1. 1. 1. 1. 0. 0. 0.]
 [0. 0. 0. 1. 1. 1. 1. 1. 0. 0. 0.]
 [0. 0. 0. 1. 1. 1. 1. 1. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]]
左上角 [[0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 1. 1. 1. 1. 1.]
 [0. 0. 0. 1. 1. 1. 1. 1.]
 [0. 0. 0. 1. 1. 1. 1. 1.]
 [0. 0. 0. 1. 1. 1. 1. 1.]]
右下角 [[1. 1. 1. 1. 1. 0. 0. 0.]
 [1. 1. 1. 1. 1. 0. 0. 0.]
 [1. 1. 1. 1. 1. 0. 0. 0.]
 [1. 1. 1. 1. 1. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0.]]

元素内填充指在元素的内部上下左右填充，
比如

[[1, 1],
 [1, 1]]

填充为：

[[1, 0, 1], 
[0, 0, 0],
 [1, 0, 1]]

代码实现

import numpy as np

matrix = [[1, 1],
          [1, 1]]

zero_inserted_matrix = np.zeros((2*len(matrix)-1, 2*len(matrix[0])-1))

for i in range(len(matrix)):
    for j in range(len(matrix[0])):
        zero_inserted_matrix[2*i][2*j] = matrix[i][j]

print(zero_inserted_matrix)

输出

[[1. 0. 1.]
 [0. 0. 0.]
 [1. 0. 1.]]

转置卷积

参考：https://www.zhihu.com/question/48279880
​ 转置卷积或微步幅卷积。但是，需要指出去卷积这个名称并不是很合适，因为转置卷积并非信号/图像处理领域定义的那种真正的去卷积。从技术上讲，信号处理中的去卷积是卷积运算的逆运算。但这里却不是这种运算。后面我们会介绍为什么将这种运算称为转置卷积更自然且更合适。

​ 我们可以使用常见卷积实现转置卷积。这里我们用一个简单的例子来说明，输入层为2∗2(下面蓝色的部分)，先进行填充值Padding为2∗2单位步长的零填充（下面在蓝色上下左右填充2行2列），再使用步长Stride为1的3∗3卷积核进行卷积操作（卷积一次获得一个值）则实现了上采样，上采样输出的大小为4∗4 也就是（6-3+1，6-3+1）

值得一提的是，可以通过各种填充和步长，我们可以将同样的2∗2输入映射到不同的图像尺寸。下图，转置卷积被应用在同一张2∗2的输入上（输入之间插入了一个零，并且周围加了2∗2的单位步长的零填充）上应用3∗3的卷积核，得到的结果（即上采样结果）大小为5∗5

通过观察上述例子中的转置卷积能够帮助我们构建起一些直观的认识。但为了进一步应用转置卷积，我们还需要了解计算机的矩阵乘法是如何实现的。从实现过程的角度我们可以理解为何转置卷积才是最合适的名称。

​ 在卷积中，我们这样定义：用C代表卷积核，input为输入图像，output为输出图像。经过卷积（矩阵乘法）后，我们将input从大图像下采样为小图像output。这种矩阵乘法实现遵循C∗input=output。

​ 下面的例子展示了这种运算在计算机内的工作方式。它将输入平展（16∗1）矩阵，并将卷积核转换为一个稀疏矩阵、（4∗16）。然后，在稀疏矩阵和平展的输入之间使用矩阵乘法。之后，再将所得到的矩阵（4∗1)转为2∗2输出。

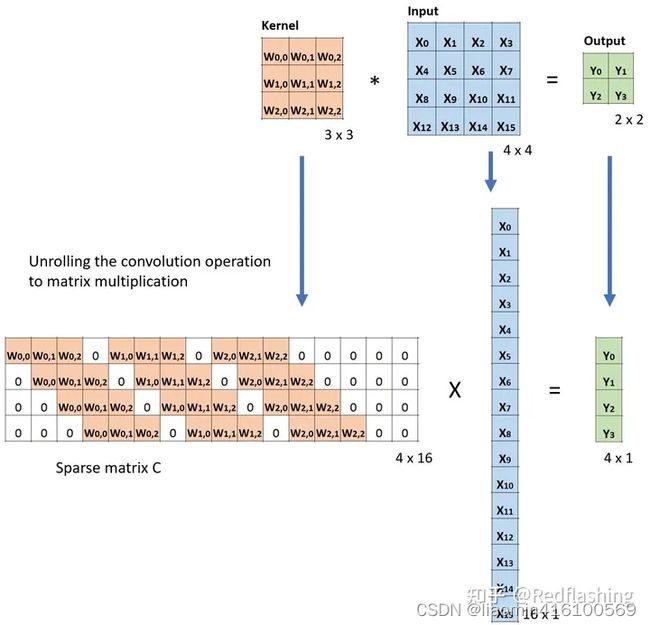
此时，若用卷积核对应稀疏矩阵的转置$C^T$（16∗4）乘以输出的平展（4∗1）所得到的结果（16∗1）的形状和输入的形状（16∗1）相同。

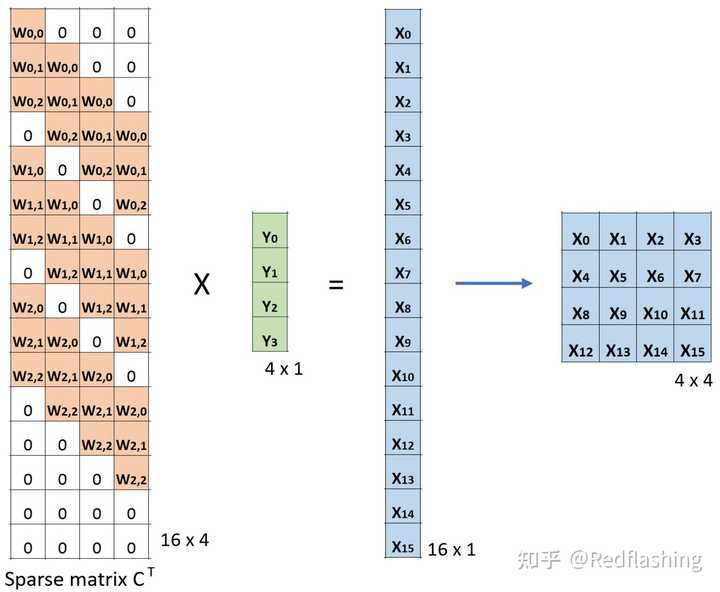
但值得注意的是，上述两次操作并不是可逆关系，对于同一个卷积核（因非其稀疏矩阵不是正交矩阵，结果转置操作之后并不能恢复到原始的数值，而仅仅保留原始的形状，所以转置卷积的名字由此而来。并回答了上面提到的疑问，相比于逆卷积而言转置卷积更加准确。

生成动漫图像

使用DCGAN训练一个模型用于生成64*64动漫图像,并通过这个例子规划神经网络的目录结构组织，大部分的开源项目的目录结构相似，以后分析开源model更加容易。

算力选择

由于gan训练需要的资源较大，时间较长，建议使用gpu服务器
gpt云平台上提供的GPU型号很多。我们按照GPU架构大致分为五类（推荐autodl或者inscode，可以按时计费，用完就释放）：

1. NVIDIA Pascal架构的GPU，如TitanXp，GTX 10系列等。 这类GPU缺乏低精度的硬件加速能力，但却具备中等的单精度算力。由于价格便宜，适合用来练习训练小模型(如Cifar10)或调试模型代码。
2. NVIDIA Volta/Turing架构的GPU，如GTX 20系列, Tesla V100等。 这类GPU搭载专为低精度(int8/float16)计算加速的TensorCore, 但单精度算力相较于上代提升不大。我们建议在实例上启用深度学习框架的混合精度训练来加速模型计算。 相较于单精度训练，混合精度训练通常能够提供2倍以上的训练加速。
3. NVIDIA Ampere架构的GPU，如GTX 30系列，Tesla A40/A100等。 这类GPU搭载第三代TensorCore。相较于前一代，支持了TensorFloat32格式，可直接加速单精度训练 (PyTorch已默认开启)。但我们仍建议使用超高算力的float16半精度训练模型，可获得比上一代GPU更显著的性能提升。
4. 寒武纪 MLU 200系列加速卡。 暂不支持模型训练。使用该系列加速卡进行模型推理需要量化为int8进行计算。 并且需要安装适配寒武纪MLU的深度学习框架。
5. 华为 Ascend 系列加速卡。 支持模型训练及推理。但需安装MindSpore框架进行计算。

GPU型号的选择并不困难。对于常用的深度学习模型，根据GPU对应精度的算力可大致推算GPU训练模型的性能。AutoDL平台标注并排名了每种型号GPU的算力，方便大家选择适合自己的GPU。

GPU的数量选择与训练任务有关。一般我们认为模型的一次训练应当在24小时内完成，这样隔天就能训练改进之后的模型。以下是选择多GPU的一些建议：

• 1块GPU。适合一些数据集较小的训练任务，如Pascal VOC等。
• 2块GPU。同单块GPU，但是你可以一次跑两组参数或者把Batchsize扩大。
• 4块GPU。适合一些中等数据集的训练任务，如MS COCO等。
• 8块GPU。经典永流传的配置！适合各种训练任务，也非常方便复现论文结果。
• 我要更多！用于训练大参数模型、大规模调参或超快地完成模型训练。

我常用的gpu按照性能从高到低的顺序，这些机器的GPU算力排名如下，并附上它们的基本配置信息：

1. A100：
   • CUDA核心数：6912
   • Tensor核心数：432
   • 显存容量：40 GB
   • 内存带宽：1555 GB/s
   • 架构：Ampere
2. V100：
   • CUDA核心数：5120
   • Tensor核心数：640
   • 显存容量：16 GB / 32 GB / 32 GB HBM2
   • 内存带宽：900 GB/s / 1134 GB/s / 1134 GB/s
   • 架构：Volta
3. P100：
   • CUDA核心数：3584
   • Tensor核心数：0
   • 显存容量：16 GB / 12 GB HBM2
   • 内存带宽：732 GB/s / 549 GB/s
   • 架构：Pascal
4. Tesla T4：
   • CUDA核心数：2560
   • Tensor核心数：320
   • 显存容量：16 GB
   • 内存带宽：320 GB/s
   • 架构：Turing
5. RTX A4000：
   • CUDA核心数：6144
   • Tensor核心数：192
   • 显存容量：16 GB
   • 内存带宽：448 GB/s
   • 架构：Ampere
     使用P100训练完大概1个小时（3831.2s）

数据集

kagle上：https://www.kaggle.com/code/splcher/starter-anime-face-dataset
邮箱注册个账号即可下载，数据集下有不同的用户基于数据集的训练代码和结果。
参考代码：https://www.kaggle.com/code/splcher/starter-anime-face-dataset

目录规划

其中各个文件的主要内容和作用如下。

• checkpoints/：用于保存训练好的模型，可使程序在异常退出后仍能重新载入模型，恢复训练。
• data/：数据相关操作，包括数据预处理、dataset实现等。
• models/：模型定义，可以有多个模型，例如上面的AlexNet和ResNet34，一个模型对应一个文件。
• utils/：可能用到的工具函数，本次实验中主要封装了可视化工具。
• config.py：配置文件，所有可配置的变量都集中在此，并提供默认值。
• main.py：主文件，训练和测试程序的入口，可通过不同的命令来指定不同的操作和参数。
• requirements.txt：程序依赖的第三方库。
• README.md：提供程序的必要说明。

源代码

数据源加载

将下载好的AnimeFaceDataset添加到data目录，新建dataset.py用于加载数据集

from torch.utils.data import Dataset,DataLoader
from torchvision import datasets, transforms
class AtomicDataset(Dataset):
    def __init__(self,root,image_size):
        Dataset.__init__(self)
        self.dataset=datasets.ImageFolder(root,
                           transform=transforms.Compose([
                               transforms.Resize(image_size),
                               transforms.CenterCrop(image_size),
                               transforms.ToTensor(),
                               transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5)),
                           ]))
    def __getitem__(self,index):
        return self.dataset[index]
    def __len__(self):
        return len(self.dataset)

    def toBatchLoader(self,batch_size):
        return DataLoader(self,batch_size=batch_size, shuffle=False)

定义配置类

config.py定义配置类

class Config:
    #定义转换后图像的大小
    img_size=64
    #训练图片所在目录，目录必须是有子目录，子目录名称就是分类名
    img_root="./data/AnimeFaceDataset"
    #每次加载的批次数
    batch_size=64
    """
    在卷积神经网络中，这些缩写通常表示以下含义：
        nz：表示输入噪声向量的维度。全称为"noise dimension"，即噪声维度。
        ngf：表示生成器网络中特征图的通道数。全称为"number of generator features"，即生成器特征图通道数。
        nc：表示输入图像的通道数。全称为"number of image channels"，即图像通道数。
    """
    #表示噪声的维度，一般是(100,1,1)
    nz=100
    #表示生成特征图的维度,64*64的图片
    ngf=64
    #生成或者传入图片的通道数
    nc=3
    # 表示判别器输入特征图的维度,64*64的图片
    ndf = 64
    # 优化器的学习率
    lr = 0.0002
    # Beta1 hyperparam for Adam optimizers
    beta1 = 0.5
    # epochs的次数
    num_epochs=50
    def __init__(self,kv):
        for key, value in kv.items():
            setattr(self, key, value)

由于这些配置默认是静态的，可以使用fire将参数定义到命令行，通过

python main.py 函数名 --参数值1=值1 --参数值2=值2的方式传入到**kwargs

main.py定义train方式

def train(**kwargs):
	print(kwargs)
if __name__ == "__main__":
    # 将main.py中所有的函数映射成  python main.py 方法名 --参数1=参数值 --参数2=参数值的形式，这些参数以keyvalue字典的形式传入kwargs
    fire.Fire()

定义模型

在models目录下新建models.py定义G和D模型

import torch.nn as nn
"""
nn.ConvTranspose2d的参数包括：
    in_channels：输入通道数
    out_channels：输出通道数
    kernel_size：卷积核大小
    stride：步长
    padding：填充大小
    output_padding：输出填充大小
    groups：分组卷积数量，默认为1
    bias：是否使用偏置，默认为True
  生成器的目标是从一个随机噪声向量生成逼真的图像。在生成器中，通道数从大到小可以理解为从抽象的特征逐渐转化为具体的图像细节。通过逐层转置卷积（ConvTranspose2d）操作，
将低维度的特征逐渐转化为高维度的图像。通道数的减少可以理解为对特征进行提取和压缩，以生成更具细节和逼真度的图像。
"""
#生成网络
class Generator(nn.Module):
    def __init__(self, nz,ngf,nc):
        super(Generator, self).__init__()
        self.main = nn.Sequential(
            # nz表示噪声的维度，一般是(100,1,1)
            # ngf表示生成特征图的维度
            # nc表示输入或者输出图像的维度
            #输出尺寸 = (输入尺寸（高度） - 1) * stride - 2 * padding + kernel_size + output_padding
            #如果（卷积核,步长，填充）=(4, 1, 0)表示图像的维度是卷积核的大小（卷积核高,卷积核宽）
            #如果（卷积核,步长，填充）=(4, 2, 1)表示图像的维度是是上一个图像的2被（输入图像高度*2,输入图像宽度*2）
            nn.ConvTranspose2d(nz, ngf * 8, 4, 1, 0, bias=False),
            nn.BatchNorm2d(ngf * 8),
            nn.ReLU(True),
            # state size. (ngf*8) x 4 x 4
            nn.ConvTranspose2d(ngf * 8, ngf * 4, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ngf * 4),
            nn.ReLU(True),
            # state size. (ngf*4) x 8 x 8
            nn.ConvTranspose2d(ngf * 4, ngf * 2, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ngf * 2),
            nn.ReLU(True),
            # state size. (ngf*2) x 16 x 16
            nn.ConvTranspose2d(ngf * 2, ngf, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ngf),
            nn.ReLU(True),
            # state size. (ngf) x 32 x 32
            nn.ConvTranspose2d(ngf, nc, 4, 2, 1, bias=False),
            nn.Tanh()
            # state size. (nc) x 64 x 64
        )

    def forward(self, input):
        return self.main(input)

"""
    和转置卷积相反的是（4,2,1）会让维度2倍降低
    卷积过程是height-kerel+1
"""
class Discriminator(nn.Module):
    def __init__(self, nc,ndf):
        super(Discriminator, self).__init__()
        self.main = nn.Sequential(
            # input is (nc) x 64 x 64
            nn.Conv2d(nc, ndf, 4, 2, 1, bias=False),
            nn.LeakyReLU(0.2, inplace=True),
            # state size. (ndf) x 32 x 32
            nn.Conv2d(ndf, ndf * 2, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ndf * 2),
            nn.LeakyReLU(0.2, inplace=True),
            # state size. (ndf*2) x 16 x 16
            nn.Conv2d(ndf * 2, ndf * 4, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ndf * 4),
            nn.LeakyReLU(0.2, inplace=True),
            # state size. (ndf*4) x 8 x 8
            nn.Conv2d(ndf * 4, ndf * 8, 4, 2, 1, bias=False),
            nn.BatchNorm2d(ndf * 8),
            nn.LeakyReLU(0.2, inplace=True),
            # state size. (ndf*8) x 4 x 4
            nn.Conv2d(ndf * 8, 1, 4, 1, 0, bias=False),
            nn.Sigmoid()
            # state size （1,1,1）
        )

    def forward(self, input):
        return self.main(input)

训练

训练D模型，让输出的数据和1比较计算损失，让损失最小化，G生成的数据使用D模型预测和0比较（骗不过）计算损失，让损失最小化。
训练G模型，生成的图片，使用D模型预测，和1比较（骗过D模型）损失，让损失最小化

def train(**kwargs):
    # 通过传入的参数初始化Config
    defaultConfig = Config(kwargs)
    # 通过给定的目录和图像大小转换成数据集
    dataset = AtomicDataset(defaultConfig.img_root, defaultConfig.img_size)
    # 转换为可迭代的批次为defaultConfig.batch_size的数据集
    dataloader = dataset.toBatchLoader(defaultConfig.batch_size)
    # 创建生成网络模型
    netG = Generator(defaultConfig.nz, defaultConfig.ngf, defaultConfig.nc).to(device)
    # 创建分类器模型
    netD = Discriminator(defaultConfig.nc, defaultConfig.ndf).to(device)
    # 使用criterion = nn.BCELoss()
    criterion = nn.BCELoss()
    # Setup Adam optimizers for both G and D
    optimizerD = optim.Adam(netD.parameters(), lr=defaultConfig.lr, betas=(defaultConfig.beta1, 0.999))
    optimizerG = optim.Adam(netG.parameters(), lr=defaultConfig.lr, betas=(defaultConfig.beta1, 0.999))
    # 如果是真的图片label=1，伪造的图片为0
    real_label = 1
    fake_label = 0
    # Lists to keep track of progress
    img_list = []
    G_losses = []
    D_losses = []
    iters = 0
    #生成一个64批次100*1*1的噪声
    fixed_noise = torch.randn(64, defaultConfig.nz, 1, 1, device=device)

    print("Starting Training Loop...")
    # For each epoch
    for epoch in range(defaultConfig.num_epochs):
        # For each batch in the dataloader
        for i, data in enumerate(dataloader, 0):

            ############################
            # (1) Update D network: maximize log(D(x)) + log(1 - D(G(z)))
            # 对于真实传入的图片进行判断器训练，label肯定是1
            # 对于噪声传入的图片进行判断器训练，label肯定是0
            ###########################
            ## 通过真实图片训练D网络
            netD.zero_grad()
            # 将64批次数据转换为gpu设备
            real_cpu = data[0].to(device)
            # 获取批次的个数
            b_size = real_cpu.size(0)
            # 生成的是一个一维的张量，其中包含64个元素,每个元素的值为1。
            label = torch.full((b_size,), real_label, device=device).float()
            # 分类器捲積后最后产生一个64个批次的1*1，转换成1维数组。
            output = netD(real_cpu).view(-1)
            # 计算和真实数据的损失
            errD_real = criterion(output, label)
            # 反向传播计算梯度
            errD_real.backward()
            # D_x的值表示判别器对真实样本的平均预测概率
            D_x = output.mean().item()

            ## 通过噪声训练生成器模型
            # 生成噪声的变量 也是64批次，噪声的通道数是100
            noise = torch.randn(b_size, defaultConfig.nz, 1, 1, device=device)
            # 传入到生成网络中，生成一张64*3*64*64的图片
            fake = netG(noise)
            # 生成器生成的图片对应的真实的label应该是0
            label.fill_(fake_label)
            # detach()是PyTorch中的一个函数，它用于从计算图中分离出一个Tensor。当我们调用detach()函数时，它会返回一个新的Tensor，该Tensor与原始Tensor共享相同的底层数据，但不会有梯度信息。
            # 使用判别器网络来判断通过噪声生成的图片，转换为1维
            output = netD(fake.detach()).view(-1)
            # 进行损失函数计算
            errD_fake = criterion(output, label)
            # 反向传播计算梯度
            errD_fake.backward()
            # 表示判别器对虚假样本的平均预测概率
            D_G_z1 = output.mean().item()
            # 将真实图片和虚假图片的损失求和获取所有的损失
            errD = errD_real + errD_fake
            # 更新权重参数
            optimizerD.step()

            ############################
            # (2) Update G network: maximize log(D(G(z)))
            # 对于G网络来说，对于虚假传入的图片进行判断器训练，尽量让判别器认为是真1，生成的图片才够真实
            ###########################
            netG.zero_grad()
            label.fill_(real_label)  # fake labels are real for generator cost
            # 使用之前的G网络生成的图片64*3*64*64,传入D网络
            output = netD(fake).view(-1)
            # 计算G网路的损失
            errG = criterion(output, label)
            # 反向计算梯度
            errG.backward()
            #表示判别器对虚假样本判断为真的的平均预测概率
            D_G_z2 = output.mean().item()
            # 更新G的权重
            optimizerG.step()

            # 输出训练统计，每1000批次
            if i % 1000 == 0:
                print('[%d/%d][%d/%d]\tLoss_D: %.4f\tLoss_G: %.4f\tD(x): %.4f\tD(G(z)): %.4f / %.4f'
                      % (epoch, defaultConfig.num_epochs, i, len(dataloader),
                         errD.item(), errG.item(), D_x, D_G_z1, D_G_z2))

            # Save Losses for plotting later
            G_losses.append(errG.item())
            D_losses.append(errD.item())

            # 即每经过一定数量的迭代（iters % 250 == 0）或者是训练的最后一个epoch的最后一个batch（(epoch == defaultConfig.num_epochs - 1) and (i == len(dataloader) - 1)），
            # 就会使用G网络通过噪声生成64批次3通道64*64的图像，并且加入到img_list去做可视化，看看效果
            if (iters % 250 == 0) or ((epoch == defaultConfig.num_epochs - 1) and (i == len(dataloader) - 1)):
                with torch.no_grad():
                    fake = netG(fixed_noise).detach().cpu()
                img_list.append(vutils.make_grid(fake, padding=2, normalize=True))

            iters += 1
    #保存生成器的网络到checkpoints目录
    torch.save(netG.state_dict(), "./checkpoints/optimizerG.pt")

可视化

绘制损失

    #绘制G和D的损失函数图像
    plt.figure(figsize=(10, 5))
    plt.title("Generator and Discriminator Loss During Training")
    #一维数组的索引值是x坐标也就是批次索引
    plt.plot(G_losses, label="G")
    plt.plot(D_losses, label="D")
    plt.xlabel("iterations")
    plt.ylabel("Loss")
    plt.legend()
    plt.show()

绘制生成器图像变化

    #创建一个8*8的画布
    fig = plt.figure(figsize=(8, 8))
    plt.axis("off")
    ims = [[plt.imshow(np.transpose(i, (1, 2, 0)), animated=True)] for i in img_list]
    ani = animation.ArtistAnimation(fig, ims, interval=1000, repeat_delay=1000, blit=True)
    HTML(ani.to_jshtml())

每250次迭代就通过G生成64图片，发现越到后面图片就越清晰。

其他项目

CycleGAN

参考地址：https://github.com/junyanz/pytorch-CycleGAN-and-pix2pix

stargan

参考地址：https://github.com/yunjey/stargan