机器学习技术(五)——特征工程与模型评估
机器学习技术(五)——特征工程与模型评估(2️⃣)
文章目录
- 机器学习技术(五)——特征工程与模型评估(:two:)
-
- 二、模型评估
-
- 1、Accuracy score
- 2、Confusion matrix混淆矩阵
-
- 1、多值
- 2、二值
- 3、Hamming loss
- 4、Precision, recall and F-measures
-
- 1、定义数据
- 2、计算Precision
- 3、计算Recall
- 4、计算F-score
- 5、Classification report:分类结果统计报告
- 6、:star::star::star:模型验证相关的公式及使用
-
- 1、加入正则化项后的代价函数
- 2、L1正则化
- 3、L2正则化
- 4、LASSO回归
- 5、平均绝对误差MAE公式、代码
- 6、均方误差MSE
- 7、均方根误差RMSE公式、代码
- 8、R平方值
- 7、交叉验证
-
- 1、交叉验证迭代器
- 2、基于类标签、具有分层的交叉验证迭代器
- 3、用于分组数据的交叉验证迭代器
- 4、时间序列分割
- 5、简单交叉验证Hold-Out-Method
- 6、K折交叉验证K-Fold-CV
- 7、留一法交叉验证LOO-CV
- 8、留P法交叉验证LPO-CV
- 8、网格搜索
-
- 1、网格搜索示例
- 2、Grid Search with Cross Validation
- 9、学习曲线
- 10、验证曲线
- 总结
机器学习技术(四)包含了十二种特征工程的应用方法,主要包括标准化,特征缩放,缩放有离群的值的数据,非线性转换,样本归一化,特征二值化,one-hot编码,缺失值插补以及生成多项式特征等步骤。
通过这些步骤可以显著提高数据的质量。同时,实验包含了基于Python代码的对特征集进行筛选的多种方法。一个典型的机器学习任务,是通过样本的特征来预测样本所对应的值。而现实中的情况往往是特征太多了,需要减少一些特征。
减少特征具有重要的现实意义,不仅减少过拟合、减少特征数量(降维)、提高模型泛化能力,而且还可以使模型获得更好的解释性,增强对特征和特征值之间的理解,加快模型的训练速度,一般的,还会获得更好的性能。基于sklearn自带数据集iris,应用多种特征筛选方法进行特征选择。
包含关于几个评估模型指标的参数计算及其原理。在日常业务有中,当我们训练模型时常常需要在多个模型中选择出最优模型,因此本实验中precision, recall rate等参数就成为评判的依据,帮助我们选择和评价模型表现。
二、模型评估
1、Accuracy score
预测准确率 = 预测正确的样本数 总样本数 预测准确率=\frac{预测正确的样本数}{总样本数} 预测准确率=总样本数预测正确的样本数
分类准确率分数是指所有分类正确的百分比。分类准确率这一衡量分类器的标准比较容易理解,但是它不能告诉你响应值的潜在分布,并且它也不能告诉你分类器犯错的类型。
import numpy as np
from sklearn.metrics import accuracy_score
#定义y的预测集和y的真实集,进行比较
y_pred = [0, 2, 1, 3]
y_true = [0, 1, 2, 3]
计算accuracy score
accuracy_score(y_true, y_pred)
由数据可见,只有两个样本被预测正确,分别为第一个和第四个,所以正确率为0.5
0.5
输出共有几个样本被预测正确
accuracy_score(y_true, y_pred, normalize=False)
结果如下所示。
2
2、Confusion matrix混淆矩阵
混淆矩阵就是分别统计分类模型归错类,归对类的观测值个数,然后把结果放在一个表里展示出来。这个表就是混淆矩阵。该章节中针对数据的特征类型计算混淆矩阵。
1、多值
该数据标签数量为3大于2
#导入计算方法
from sklearn.metrics import confusion_matrix
#自定义真实值以及预测值
y_true = [2, 0, 2, 2, 0, 1]
y_pred = [0, 0, 2, 2, 0, 2]
#计算混淆矩阵
confusion_matrix(y_true, y_pred)
输出结果如下,列表示预测值,行表示真实值。所以第[1,1]=2代表真实值为0,也同时被预测为0的有2个;[2,1]=0表示真实值为1但被预测为0的有0个。
array([[2, 0, 0],
[0, 0, 1],
[1, 0, 2]])
2、二值
该数据中只有两个标签0和1
#定义预测数据以及真实数据
y_true = [0, 0, 0, 1, 1, 1, 1, 1]
y_pred = [0, 1, 0, 1, 0, 1, 0, 1]
输入:
confusion_matrix(y_true, y_pred)
左上,左下,右上,右下分别为true positive(预测为1,真实为1),false negative(真实为1,预测为0),false positive(真实为0,预测为1),true negative(真实为0,实际为0)
array([[2, 1],
[2, 3]])
#查看四个值
tn, fp, fn, tp = confusion_matrix(y_true, y_pred).ravel()
tn, fp, fn, tp
(2, 1, 2, 3)
3、Hamming loss
汉明损失 = 预测错误的样本数 样本总数 汉明损失=\frac{预测错误的样本数}{样本总数} 汉明损失=样本总数预测错误的样本数
预测标签与真实标签的异或关系。汉明损失显然是越小越好
输入:
#定义预测值以及真实值
from sklearn.metrics import hamming_loss
y_pred = [1, 2, 3, 4]
y_true = [2, 2, 3, 4]
输出汉明损失
hamming_loss(y_true, y_pred)
只有一个预测错误,错误率0.25
0.25
4、Precision, recall and F-measures
三个指标基于模型预测混淆矩阵进行计算
P r e c i s i o n = T P F P + T P Precision=\frac{TP}{FP+TP} Precision=FP+TPTP
R e c a l l = T P T P + F N Recall=\frac{TP}{TP+FN} Recall=TP+FNTP
F − m e a s u r e = 2 ∗ p r e c i s i o n ∗ R e c a l l p r e c i s i o n + R e c a l l F-measure=\frac{2*precision*Recall}{precision+Recall} F−measure=precision+Recall2∗precision∗Recall
1、定义数据
#定义数据
from sklearn import metrics
y_pred = [0, 1, 0, 0]
y_true = [0, 1, 0, 1]
2、计算Precision
# precision=tp/tp+fp
metrics.precision_score(y_true, y_pred)
输出:
1.0
3、计算Recall
# recall=tp/fn+tp
metrics.recall_score(y_true, y_pred)
输出:
0.5
4、计算F-score
输入:
# F_beta = (1+beta^2)*(precision*recall/beta^2*precision+recall)
metrics.f1_score(y_true, y_pred)
输出:
0.6666666666666666
输入:
#调整beta的值以获得不同标准的fbeta score
print(metrics.fbeta_score(y_true, y_pred, beta=0.5))
print(metrics.fbeta_score(y_true, y_pred, beta=1))
print(metrics.fbeta_score(y_true, y_pred, beta=2))
输出:
0.8333333333333334
0.6666666666666666
0.5555555555555556
5、Classification report:分类结果统计报告
sklearn中的classification_report函数用于显示主要分类指标的文本报告.在报告中显示每个类的精确度,召回率,F1值等信息。
from sklearn.metrics import classification_report
y_true = [0, 1, 2, 2, 0]
y_pred = [0, 0, 2, 1, 0]
target_names = ['class 0', 'class 1', 'class 2']
print(classification_report(y_true, y_pred, target_names=target_names))
输出结果如下,是一个综合统计,其中support表示真实类别的次数,avg / total 表示各列的均值。
输出:
precision recall f1-score support
class 0 0.67 1.00 0.80 2
class 1 0.00 0.00 0.00 1
class 2 1.00 0.50 0.67 2
accuracy 0.60 5
macro avg 0.56 0.50 0.49 5
weighted avg 0.67 0.60 0.59 5
6、⭐️⭐️⭐️模型验证相关的公式及使用
1、加入正则化项后的代价函数
1 2 ∑ j = 1 N { y i − w T σ ( x j ) } 2 + λ 2 ∑ j = 1 N ∣ w j ∣ q \frac{1}{2}\sum_{j=1}^N\{y_i-w^T\sigma(x_j)\}^2+\frac{\lambda}{2}\sum_{j=1}^N|w_j|_q 21j=1∑N{yi−wTσ(xj)}2+2λj=1∑N∣wj∣q
2、L1正则化
J = J 0 + α ∑ ∣ w ∣ J=J_0+\alpha\sum |w| J=J0+α∑∣w∣
poly = PolynomialFeatures(3)
train_data_poly = poly.fit_transform(train_data)
test_data_poly = poly.transform(test_data)
clf = SGDRegressor(max_iter=1000, tol=1e-3, penalty= 'L1', alpha=0.00001)
clf.fit(train_data_poly, train_target)
score_train = mean_squared_error(train_target, clf.predict(train_data_poly))
score_test = mean_squared_error(test_target, clf.predict(test_data_poly))
print("SGDRegressor train MSE: ", score_train)
print("SGDRegressor test MSE: ", score_test)
#
SGDRegressor train MSE: 0.13511036183307598
SGDRegressor test MSE: 0.14332864452241414
3、L2正则化
J = J 0 + α ∑ w 2 J=J_0+\alpha\sum w^2 J=J0+α∑w2
poly = PolynomialFeatures(3)
train_data_poly = poly.fit_transform(train_data)
test_data_poly = poly.transform(test_data)
clf = SGDRegressor(max_iter=1000, tol=1e-3, penalty= 'L2', alpha=0.0001)
clf.fit(train_data_poly, train_target)
score_train = mean_squared_error(train_target, clf.predict(train_data_poly))
score_test = mean_squared_error(test_target, clf.predict(test_data_poly))
print("SGDRegressor train MSE: ", score_train)
print("SGDRegressor test MSE: ", score_test)
SGDRegressor train MSE: 0.13323787756476335
SGDRegressor test MSE: 0.14187259762046708
4、LASSO回归
J ( θ ) = M S E ( y , y ^ ; θ ) + α ∑ i = 1 n ∣ θ i ∣ J(\theta)=MSE(y,\hat{y};\theta)+\alpha\sum_{i=1}^n|\theta_i| J(θ)=MSE(y,y^;θ)+αi=1∑n∣θi∣
5、平均绝对误差MAE公式、代码
M A E = 1 n ∑ i = 1 n ∣ f i − y i ∣ = 1 n ∑ i = 1 n ∣ e i ∣ MAE=\frac{1}{n}\sum_{i=1}^n|f_i-y_i|=\frac{1}{n}\sum_{i=1}^n|e_i| MAE=n1i=1∑n∣fi−yi∣=n1i=1∑n∣ei∣
from sklearn.metrics import mean_absolute_error
mean_absolute_error(y_test, y_pred)
6、均方误差MSE
M S E = 1 n ∑ i = 1 n ( o b s e r v e d i − p r e d i c t e d i ) 2 MSE=\frac{1}{n}\sum_{i=1}^{n}(observed_i-predicted_i)^2 MSE=n1i=1∑n(observedi−predictedi)2
from sklearn.metrics import mean_squared_error
mean_squared_error(y_test, y_pred)
7、均方根误差RMSE公式、代码
R M S E = M S E = S S E / N = 1 n ∑ i = 1 n w i ( y i − y i ^ ) 2 RMSE=\sqrt{MSE}=\sqrt{SSE/N}=\sqrt{\frac{1}{n}\sum_{i=1}^{n}w_i(y_i-\hat{y_i})^2} RMSE=MSE=SSE/N=n1i=1∑nwi(yi−yi^)2
from sklearn.metrics import mean_squared_error
Pred_Error = mean_squared_error(y_test, y_pred)
Sqrt(Pred_Error)
8、R平方值
R 2 ( y , y ^ ) = 1 − ∑ i = 0 n s a m p l e s − 1 ( y i − y i ^ ) 2 ∑ i = 0 n s a m p l e s − 1 ( y i − y i ˉ ) 2 R^2(y,\hat{y})=1-\frac{\sum_{i=0}^{n_{samples}-1}(y_i-\hat{y_i})^2}{\sum_{i=0}^{n_{samples}-1}(y_i-\bar{y_i})^2} R2(y,y^)=1−∑i=0nsamples−1(yi−yiˉ)2∑i=0nsamples−1(yi−yi^)2
from sklearn.metrics import r2_score
r2_score(y_test, y_pred)
7、交叉验证
1、交叉验证迭代器
K折交叉验证: KFold 将所有的样例划分为 k 个组,称为折叠 (fold) (如果 k = n, 这等价于 Leave One Out(留一) 策略),都具有相同的大小(如果可能)。预测函数学习时使用 k - 1 个折叠中的数据,最后一个剩下的折叠会用于测试。
K折重复多次: RepeatedKFold 重复 K-Fold n 次。当需要运行时可以使用它 KFold n 次,在每次重复中产生不同的分割。
留一交叉验证: LeaveOneOut (或 LOO) 是一个简单的交叉验证。每个学习集都是通过除了一个样本以外的所有样本创建的,测试集是被留下的样本。 因此,对于 n 个样本,我们有 n 个不同的训练集和 n 个不同的测试集。这种交叉验证程序不会浪费太多数据,因为只有一个样本是从训练集中删除掉的:
留P交叉验证: LeavePOut 与 LeaveOneOut 非常相似,因为它通过从整个集合中删除 p 个样本来创建所有可能的 训练/测试集。对于 n 个样本,这产生了 {n \choose p} 个 训练-测试 对。与 LeaveOneOut 和 KFold 不同,当 p > 1 时,测试集会重叠。
用户自定义数据集划分: ShuffleSplit 迭代器将会生成一个用户给定数量的独立的训练/测试数据划分。样例首先被打散然后划分为一对训练测试集合。
设置每次生成的随机数相同: 可以通过设定明确的 random_state ,使得伪随机生成器的结果可以重复。
2、基于类标签、具有分层的交叉验证迭代器
如何解决样本不平衡问题? 使用StratifiedKFold和StratifiedShuffleSplit 分层抽样。 一些分类问题在目标类别的分布上可能表现出很大的不平衡性:例如,可能会出现比正样本多数倍的负样本。在这种情况下,建议采用如 StratifiedKFold 和 StratifiedShuffleSplit 中实现的分层抽样方法,确保相对的类别频率在每个训练和验证 折叠 中大致保留。
StratifiedKFold是 k-fold 的变种,会返回 stratified(分层) 的折叠:每个小集合中, 各个类别的样例比例大致和完整数据集中相同。
StratifiedShuffleSplit是 ShuffleSplit 的一个变种,会返回直接的划分,比如: 创建一个划分,但是划分中每个类的比例和完整数据集中的相同。
3、用于分组数据的交叉验证迭代器
如何进一步测试模型的泛化能力? 留出一组特定的不属于测试集和训练集的数据。有时我们想知道在一组特定的 groups 上训练的模型是否能很好地适用于看不见的 group 。为了衡量这一点,我们需要确保验证对象中的所有样本来自配对训练折叠中完全没有表示的组。
GroupKFold是 k-fold 的变体,它确保同一个 group 在测试和训练集中都不被表示。 例如,如果数据是从不同的 subjects 获得的,每个 subject 有多个样本,并且如果模型足够灵活以高度人物指定的特征中学习,则可能无法推广到新的 subject 。 GroupKFold 可以检测到这种过拟合的情况。
LeaveOneGroupOut是一个交叉验证方案,它根据第三方提供的 array of integer groups (整数组的数组)来提供样本。这个组信息可以用来编码任意域特定的预定义交叉验证折叠。
每个训练集都是由除特定组别以外的所有样本构成的。
LeavePGroupsOut类似于 LeaveOneGroupOut ,但为每个训练/测试集删除与 P 组有关的样本。
GroupShuffleSplit迭代器是 ShuffleSplit 和 LeavePGroupsOut 的组合,它生成一个随机划分分区的序列,其中为每个分组提供了一个组子集。
4、时间序列分割
TimeSeriesSplit是 k-fold 的一个变体,它首先返回 k 折作为训练数据集,并且 (k+1) 折作为测试数据集。 请注意,与标准的交叉验证方法不同,连续的训练集是超越前者的超集。 另外,它将所有的剩余数据添加到第一个训练分区,它总是用来训练模型。
5、简单交叉验证Hold-Out-Method
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=.4, random_state=0)
6、K折交叉验证K-Fold-CV
from sklearn.model_selection import Kfold
kf = KFold(n_splits=10)
7、留一法交叉验证LOO-CV
from sklearn.model_selection import LeaveOneOut
loo = LeaveOneOut()
8、留P法交叉验证LPO-CV
from sklearn.model_selection import LeavePOut
lpo = LeavePOut(p=5)
数据分割算法实例
from sklearn.model_selection import train_test_split # 交叉验证所需的函数
from sklearn.model_selection import cross_val_score # 交叉验证所需的函数
from sklearn.model_selection import cross_validate # 交叉验证所需的函数
from sklearn.model_selection import KFold, LeaveOneOut
from sklearn.model_selection import LeavePOut, ShuffleSplit
# 交叉验证所需的子集划分方法
from sklearn.model_selection import StratifiedKFold # 分层分割
from sklearn.model_selection import StratifiedShuffleSplit # 分层分割
from sklearn.model_selection import GroupKFold, LeaveOneGroupOut
from sklearn.model_selection import LeavePGroupsOut, GroupShuffleSplit
from sklearn.model_selection import TimeSeriesSplit
# 时间序列分割
from sklearn import datasets # 自带数据集
from sklearn import svm # SVM算法
from sklearn import preprocessing # 预处理模块
from sklearn.metrics import recall_score # 模型度量
iris = datasets.load_iris() # 加载数据集
print('样本集大小:', iris.data.shape, iris.target.shape)
# =====数据集划分,训练模型=====
X_train, X_test, y_train, y_test = train_test_split(
iris.data, iris.target, test_size=0.4,
random_state=0) # 交叉验证划分训练集和测试集.test_size为测试集所占的比例
print('训练集大小:', X_train.shape, y_train.shape) # 训练集样本大小
print('测试集大小:', X_test.shape, y_test.shape) # 测试集样本大小
clf = svm.SVC(kernel='linear', C=1).fit(X_train, y_train) # 使用训练集训练模型
print('准确率:', clf.score(X_test, y_test)) # 计算测试集的度量值(准确率)
# 如果涉及到归一化,则在测试集上也要使用训练集模型提取的归一化函数。
scaler = preprocessing.StandardScaler().fit(
X_train) # 通过训练集获得归一化函数模型。(也就是先减几,再除以几的函数)。在训练集和测试集上都使用这个归一化函数
X_train_transformed = scaler.transform(X_train)
clf = svm.SVC(kernel='linear', C=1).fit(X_train_transformed,
y_train) # 使用训练集训练模型
X_test_transformed = scaler.transform(X_test)
print(clf.score(X_test_transformed, y_test)) # 计算测试集的度量值(准确度)
# =====直接调用交叉验证评估模型=====
clf = svm.SVC(kernel='linear', C=1)
scores = cross_val_score(clf, iris.data, iris.target, cv=5) #cv为迭代次数。
print(scores) # 打印输出每次迭代的度量值(准确度)
print("Accuracy: %0.2f (+/- %0.2f)" %
(scores.mean(), scores.std() * 2)) # 获取置信区间。(也就是均值和方差)
# =====多种度量结果=====
scoring = ['precision_macro',
'recall_macro'] # precision_macro为精度,recall_macro为召回率
scores = cross_validate(clf,
iris.data,
iris.target,
scoring=scoring,
cv=5,
return_train_score=True)
sorted(scores.keys())
print('测试结果:', scores) # scores类型为字典。包含训练得分,拟合次数, score-times (得分次数)
# =====K折交叉验证、留一交叉验证、留p交叉验证、随机排列交叉验证=====
# k折划分子集
kf = KFold(n_splits=2)
for train, test in kf.split(iris.data):
print("k折划分:%s %s" % (train.shape, test.shape))
break
# 留一划分子集
loo = LeaveOneOut()
for train, test in loo.split(iris.data):
print("留一划分:%s %s" % (train.shape, test.shape))
break
# 留p划分子集
lpo = LeavePOut(p=2)
for train, test in loo.split(iris.data):
print("留p划分:%s %s" % (train.shape, test.shape))
break
# 随机排列划分子集
ss = ShuffleSplit(n_splits=3, test_size=0.25, random_state=0)
for train_index, test_index in ss.split(iris.data):
print("随机排列划分:%s %s" % (train.shape, test.shape))
break
# =====分层K折交叉验证、分层随机交叉验证=====
skf = StratifiedKFold(n_splits=3) #各个类别的比例大致和完整数据集中相同
for train, test in skf.split(iris.data, iris.target):
print("分层K折划分:%s %s" % (train.shape, test.shape))
break
skf = StratifiedShuffleSplit(n_splits=3) # 划分中每个类的比例和完整数据集中的相同
for train, test in skf.split(iris.data, iris.target):
print("分层随机划分:%s %s" % (train.shape, test.shape))
break
# =====组 k-fold交叉验证、留一组交叉验证、留 P 组交叉验证、Group Shuffle Split=====
X = [0.1, 0.2, 2.2, 2.4, 2.3, 4.55, 5.8, 8.8, 9, 10]
y = ["a", "b", "b", "b", "c", "c", "c", "d", "d", "d"]
groups = [1, 1, 1, 2, 2, 2, 3, 3, 3, 3]
# k折分组
gkf = GroupKFold(n_splits=3) # 训练集和测试集属于不同的组
for train, test in gkf.split(X, y, groups=groups):
print("组 k-fold分割:%s %s" % (train, test))
# 留一分组
logo = LeaveOneGroupOut()
for train, test in logo.split(X, y, groups=groups):
print("留一组分割:%s %s" % (train, test))
# 留p分组
lpgo = LeavePGroupsOut(n_groups=2)
for train, test in lpgo.split(X, y, groups=groups):
print("留 P 组分割:%s %s" % (train, test))
# 随机分组
gss = GroupShuffleSplit(n_splits=4, test_size=0.5, random_state=0)
for train, test in gss.split(X, y, groups=groups):
print("随机分割:%s %s" % (train, test))
# =====时间序列分割=====
tscv = TimeSeriesSplit(n_splits=3)
TimeSeriesSplit(max_train_size=None, n_splits=3)
for train, test in tscv.split(iris.data):
print("时间序列分割:%s %s" % (train, test))
输出如下:
样本集大小: (150, 4) (150,)
训练集大小: (90, 4) (90,)
测试集大小: (60, 4) (60,)
准确率: 0.9666666666666667
0.9333333333333333
[0.9666666667 1. 0.9666666667 0.9666666667 1. ]
Accuracy: 0.98 (+/- 0.03)
测试结果: {'fit_time': array([0.0007252693, 0.0003640652, 0.0003199577, 0.0004220009, 0.000346899 ]), 'score_time': array([0.0010209084, 0.0009698868, 0.0009701252, 0.0010108948, 0.0009820461]), 'test_precision_macro': array([0.9696969697, 1. , 0.9696969697, 0.9696969697, 1. ]), 'train_precision_macro': array([0.976744186 , 0.976744186 , 0.9918699187, 0.9841269841, 0.9833333333]), 'test_recall_macro': array([0.9666666667, 1. , 0.9666666667, 0.9666666667, 1. ]), 'train_recall_macro': array([0.975 , 0.975 , 0.9916666667, 0.9833333333, 0.9833333333])}
k折划分:(75,) (75,)
留一划分:(149,) (1,)
留p划分:(149,) (1,)
随机排列划分:(149,) (1,)
分层K折划分:(99,) (51,)
分层随机划分:(135,) (15,)
组 k-fold分割:[0 1 2 3 4 5] [6 7 8 9]
组 k-fold分割:[0 1 2 6 7 8 9] [3 4 5]
组 k-fold分割:[3 4 5 6 7 8 9] [0 1 2]
留一组分割:[3 4 5 6 7 8 9] [0 1 2]
留一组分割:[0 1 2 6 7 8 9] [3 4 5]
留一组分割:[0 1 2 3 4 5] [6 7 8 9]
留 P 组分割:[6 7 8 9] [0 1 2 3 4 5]
留 P 组分割:[3 4 5] [0 1 2 6 7 8 9]
留 P 组分割:[0 1 2] [3 4 5 6 7 8 9]
随机分割:[0 1 2] [3 4 5 6 7 8 9]
随机分割:[3 4 5] [0 1 2 6 7 8 9]
随机分割:[3 4 5] [0 1 2 6 7 8 9]
随机分割:[3 4 5] [0 1 2 6 7 8 9]
时间序列分割:[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38] [39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75]
时间序列分割:[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48
49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75] [ 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112]
时间序列分割:[ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36
37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73
74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110
111 112] [113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149]
8、网格搜索
交叉验证经常与网格搜索进行结合,作为参数评价的一种方法,这种方法叫做grid search with cross validation。sklearn因此设计了一个这样的类GridSearchCV,这个类实现了fit,predict,score等方法,被当做了一个estimator,使用fit方法,该过程中:
(1)搜索到最佳参数;
(2)实例化了一个最佳参数的estimator;
1、网格搜索示例
from sklearn.datasets import load_iris
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
iris = load_iris()
X_train, X_test, y_train, y_test = train_test_split(iris.data,
iris.target,
random_state=0)
print("Size of training set:{} size of testing set:{}".format(
X_train.shape[0], X_test.shape[0]))
#### grid search start
best_score = 0
for gamma in [0.001, 0.01, 0.1, 1, 10, 100]:
for C in [0.001, 0.01, 0.1, 1, 10, 100]:
svm = SVC(gamma=gamma, C=C) #对于每种参数可能的组合,进行一次训练;
svm.fit(X_train, y_train)
score = svm.score(X_test, y_test)
if score > best_score: #找到表现最好的参数
best_score = score
best_parameters = {'gamma': gamma, 'C': C}
#### grid search end
print("Best score:{:.2f}".format(best_score))
print("Best parameters:{}".format(best_parameters))
输出结果:
Size of training set:112 size of testing set:38
Best score:0.97
Best parameters:{'gamma': 0.001, 'C': 100}
2、Grid Search with Cross Validation
X_trainval,X_test,y_trainval,y_test = train_test_split(iris.data,iris.target,random_state=0)
X_train,X_val,y_train,y_val = train_test_split(X_trainval,y_trainval,random_state=1)
print("Size of training set:{} size of validation set:{} size of testing set:{}".format(X_train.shape[0],X_val.shape[0],X_test.shape[0]))
best_score = 0.0
for gamma in [0.001,0.01,0.1,1,10,100]:
for C in [0.001,0.01,0.1,1,10,100]:
svm = SVC(gamma=gamma,C=C)
svm.fit(X_train,y_train)
score = svm.score(X_val,y_val)
if score > best_score:
best_score = score
best_parameters = {'gamma':gamma,'C':C}
svm = SVC(**best_parameters) #使用最佳参数,构建新的模型
svm.fit(X_trainval,y_trainval) #使用训练集和验证集进行训练,more data always results in good performance.
test_score = svm.score(X_test,y_test) # evaluation模型评估
print("Best score on validation set:{:.2f}".format(best_score))
print("Best parameters:{}".format(best_parameters))
print("Best score on test set:{:.2f}".format(test_score))
输出结果:
Size of training set:84 size of validation set:28 size of testing set:38
Best score on validation set:0.96
Best parameters:{'gamma': 0.001, 'C': 10}
Best score on test set:0.92
sklearn方法:
from sklearn.model_selection import cross_val_score
best_score = 0.0
for gamma in [0.001,0.01,0.1,1,10,100]:
for C in [0.001,0.01,0.1,1,10,100]:
svm = SVC(gamma=gamma,C=C)
scores = cross_val_score(svm,X_trainval,y_trainval,cv=5) #5折交叉验证
score = scores.mean() #取平均数
if score > best_score:
best_score = score
best_parameters = {"gamma":gamma,"C":C}
svm = SVC(**best_parameters)
svm.fit(X_trainval,y_trainval)
test_score = svm.score(X_test,y_test)
print("Best score on validation set:{:.2f}".format(best_score))
print("Best parameters:{}".format(best_parameters))
print("Score on testing set:{:.2f}".format(test_score))
from sklearn.model_selection import GridSearchCV
#把要调整的参数以及其候选值 列出来;
param_grid = {"gamma":[0.001,0.01,0.1,1,10,100],
"C":[0.001,0.01,0.1,1,10,100]}
print("Parameters:{}".format(param_grid))
grid_search = GridSearchCV(SVC(),param_grid,cv=5) #实例化一个GridSearchCV类
X_train,X_test,y_train,y_test = train_test_split(iris.data,iris.target,random_state=10)
grid_search.fit(X_train,y_train) #训练,找到最优的参数,同时使用最优的参数实例化一个新的SVC estimator。
print("Test set score:{:.2f}".format(grid_search.score(X_test,y_test)))
print("Best parameters:{}".format(grid_search.best_params_))
print("Best score on train set:{:.2f}".format(grid_search.best_score_))
输出:
Parameters:{'gamma': [0.001, 0.01, 0.1, 1, 10, 100], 'C': [0.001, 0.01, 0.1, 1, 10, 100]}
Test set score:0.97
Best parameters:{'C': 10, 'gamma': 0.1}
Best score on train set:0.98
9、学习曲线
学习曲线用于观察模型在训练集和验证集上的表现随着训练样本数量的增加而变化的情况,帮助我们判断是否存在过拟合或欠拟合问题;
import numpy as np
import matplotlib.pyplot as plt
from sklearn.naive_bayes import GaussianNB
from sklearn.svm import SVC
from sklearn.datasets import load_digits
from sklearn.model_selection import learning_curve
from sklearn.model_selection import ShuffleSplit
def plot_learning_curve(estimator, title, X, y, ylim=None, cv=None,
n_jobs=1, train_sizes=np.linspace(.1, 1.0, 5)):
plt.figure()
plt.title(title)
if ylim is not None:
plt.ylim(*ylim)
plt.xlabel("Training examples")
plt.ylabel("Score")
train_sizes, train_scores, test_scores = learning_curve(
estimator, X, y, cv=cv, n_jobs=n_jobs, train_sizes=train_sizes)
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)
plt.grid()
plt.fill_between(train_sizes, train_scores_mean - train_scores_std,
train_scores_mean + train_scores_std, alpha=0.1,
color="r")
plt.fill_between(train_sizes, test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std, alpha=0.1, color="g")
plt.plot(train_sizes, train_scores_mean, 'o-', color="r",
label="Training score")
plt.plot(train_sizes, test_scores_mean, 'o-', color="g",
label="Cross-validation score")
plt.legend(loc="best")
return plt
digits = load_digits()
X, y = digits.data, digits.target
title = "Learning Curves (Naive Bayes)"
# Cross validation with 100 iterations to get smoother mean test and train
# score curves, each time with 20% data randomly selected as a validation set.
cv = ShuffleSplit(n_splits=100, test_size=0.2, random_state=0)
estimator = GaussianNB()
plot_learning_curve(estimator, title, X, y, ylim=(0.7, 1.01), cv=cv, n_jobs=4)
title = "Learning Curves (SVM, RBF kernel, $\gamma=0.001$)"
# SVC is more expensive so we do a lower number of CV iterations:
cv = ShuffleSplit(n_splits=10, test_size=0.2, random_state=0)
estimator = SVC(gamma=0.001)
plot_learning_curve(estimator, title, X, y, (0.7, 1.01), cv=cv, n_jobs=4)
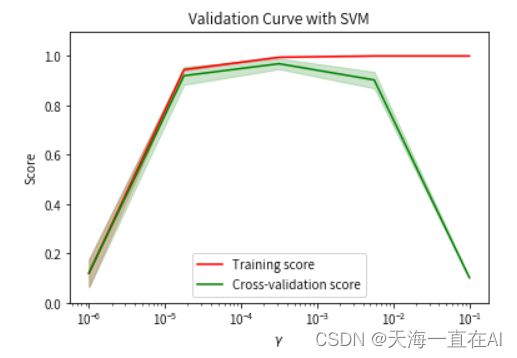
10、验证曲线
验证曲线用于评估模型在不同超参数取值下的性能,帮助我们选择最佳的超参数取值。
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import load_digits
from sklearn.svm import SVC
#from sklearn.learning_curve import validation_curve
from sklearn.model_selection import validation_curve
digits = load_digits()
X, y = digits.data, digits.target
param_range = np.logspace(-6, -1, 5)
train_scores, test_scores = validation_curve(
SVC(), X, y, param_name="gamma", param_range=param_range,
cv=10, scoring="accuracy", n_jobs=1)
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)
plt.title("Validation Curve with SVM")
plt.xlabel("$\gamma$")
plt.ylabel("Score")
plt.ylim(0.0, 1.1)
plt.semilogx(param_range, train_scores_mean, label="Training score", color="r")
plt.fill_between(param_range, train_scores_mean - train_scores_std,
train_scores_mean + train_scores_std, alpha=0.2, color="r")
plt.semilogx(param_range, test_scores_mean, label="Cross-validation score",
color="g")
plt.fill_between(param_range, test_scores_mean - test_scores_std,
test_scores_mean + test_scores_std, alpha=0.2, color="g")
plt.legend(loc="best")
plt.show()
总结
可以更加了解如何去评价模型表现以及如何去选择模型的的原理,为后续数据挖掘工作了解更深。