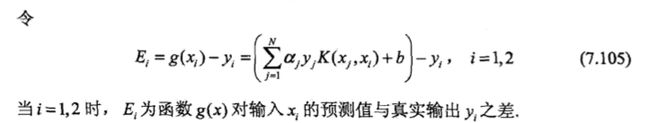ML刻意练习第三周之SVM

SVM有很多实现，本文只介绍其中最流行的一种实现：序列最小优化（SMO）算法。之后引入核函数（kernel）将只能进行线性分类的SVM扩展为非线性分类器。
关于具体的理论推导可以查阅统计学习方法（李航著）。
序列最小优化（SMO）算法是将大的优化问题分解为多个小的优化问题来求解的。其原理是每次循环中选择两个alpha进行优化处理。一旦找到一对合适的alpha，那么增大其中一个并减小另外一个。合适是指满足下面两个条件：1.这两个alpha必须在间隔边界之外；2.这两个alpha还没有进行过区间处理或者不在边界上。

一、简化版的SMO算法

简化版的SMO算法跳过了外循环确定要优化的最佳alpha对这一步骤。

1.构造辅助函数
因为我们要同时改变两个alpha，因此我们需要构造两个辅助函数：
①.首先载入文件

def loadDataSet(fileName):
    dataMat = []; labelMat = []
    fr = open(fileName)
    for line in fr.readlines():
        lineArr = line.strip().split('\t')
        dataMat.append([float(lineArr[0]), float(lineArr[1])])
        labelMat.append(float(lineArr[2]))
    return dataMat,labelMat

②.辅助函数之一：随机选择一个与 i 不相等的整数 j 。

def selectJrand(i,m):   #返回一个与i不相等的j，i为第一个a的下标，m为a的个数
    j=i                 
    while (j==i):
        j = int(random.uniform(0,m))
    return j

③.辅助函数之二：当数值太大或太小时对其进行调整。

def clipAlpha(aj,H,L):#返回的aj在L-H之间
    if aj > H: 
        aj = H
    if L > aj:
        aj = L
    return aj

④.测试数据集的标签：

dataMat , labelMat = loadDataSet('E:\学习资料\机器学习算法刻意练习\机器学习实战书电子版\machinelearninginaction\Ch06\\testSet.txt')
print(labelMat)

结果如下：

[-1.0, -1.0, 1.0, -1.0, 1.0, 1.0, 1.0, -1.0, -1.0, -1.0, -1.0, -1.0, -1.0, 1.0, -1.0, 1.0, 1.0, -1.0, 1.0, -1.0, -1.0, -1.0, 1.0, -1.0, -1.0, 1.0, 1.0, -1.0, -1.0, -1.0, -1.0, 1.0, 1.0, 1.0, 1.0, ...

由此可见该数据集的标签yi是用1和-1来标记的，因此不需要再做调整。

2.完成简化版的SMO算法
其代码如下所示：

def smoSimple(dataMatIn, classLabels, C, toler, maxIter):#maxIter为最大遍历次数
    dataMatrix = np.mat(dataMatIn)                       #m*n阶矩阵,m为样本个数，n为特征数
    labelMat = np.mat(classLabels).transpose()           #m*1阶矩阵
    b = 0
    m,n = np.shape(dataMatrix)
    alphas = np.mat(np.zeros((m,1)))                        #m*1阶矩阵
    iter = 0                                             #存储没有任何alphas改变的情况下遍历的次数
    while (iter < maxIter):
        alphaPairsChanged = 0                            #用于记录a值是否已经进行优化
        for i in range(m):
            fXi = float(np.multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b
            #numpy的multiply函数表示对应元素的乘积，*表示矩阵的乘法运算，之前讲过。。。。。
            #np.mat.T 与mat.transpose是一样的，都是实现矩阵的转置
            #该公式为SVM算法的决策判断函数，具体推导可以参考统计学习方法（第一版在106页的公式7-30）
            Ei = fXi - float(labelMat[i])
            if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):#如果已经在边界上的值，就不需要继续优化了
                #第一个条件是负间隔，第二个是正间隔
                j = selectJrand(i,m)
                fXj = float(np.multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[j,:].T)) + b
                #fXj = 求和（a星*yj * x* Xj的T）+b
                Ej = fXj - float(labelMat[j])
                #同样的方法计算第二个a的错误率
                alphaIold = alphas[i].copy()
                alphaJold = alphas[j].copy()                                  #存储优化前的两个a
                if (labelMat[i] != labelMat[j]):                              #L与H的求解公式请参照统计学习方法那两个图
                    L = max(0, alphas[j] - alphas[i])
                    H = min(C, C + alphas[j] - alphas[i])
                else:
                    L = max(0, alphas[j] + alphas[i] - C)
                    H = min(C, alphas[j] + alphas[i])
                if L==H: print("L==H"); continue
                eta = 2.0 * dataMatrix[i,:]*dataMatrix[j,:].T - dataMatrix[i,:]*dataMatrix[i,:].T - dataMatrix[j,:]*dataMatrix[j,:].T
                #eta = 2.0*Xi*Xj的T - Xi*Xi的T - Xj * Xj的T
                if eta >= 0: print("eta>=0"); continue
                alphas[j] -= labelMat[j]*(Ei - Ej)/eta
                alphas[j] = clipAlpha(alphas[j],H,L)
                if (abs(alphas[j] - alphaJold) < 0.00001): print("j not moving enough"); continue #当两个E差值很小时，每次走的距离太小，换其他的
                alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])#update i by the same amount as j
                                                                        #the update is in the oppostie direction
                b1 = b - Ei- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[i,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i,:]*dataMatrix[j,:].T
                b2 = b - Ej- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i,:]*dataMatrix[j,:].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j,:]*dataMatrix[j,:].T
                if (0 < alphas[i]) and (C > alphas[i]): b = b1
                elif (0 < alphas[j]) and (C > alphas[j]): b = b2
                else: b = (b1 + b2)/2.0
                alphaPairsChanged += 1
                # print("iter:{} i:{}, pairs changed {}".format(iter,i,alphaPairsChanged))
        if (alphaPairsChanged == 0): iter += 1
        else: iter = 0
        # print("iteration number:{}".format(iter))
    return b,alphas   #返回各特征的系数alphas和常数项b

因为该算法涉及较多的理论知识，所以不懂的可以参照具体的理论推导（例如：统计学习方法7.4节）来看，下面简单写一下某些代码所实现的功能。
①.计算预测值（分类预测）

fXi = float(np.multiply(alphas,labelMat).T*(dataMatrix*dataMatrix[i,:].T)) + b

以上代码使用numpy模块运用矩阵和向量的形式完成了以下公式的运算。

②.Ei和Ej的计算：

Ej = fXj - float(labelMat[j])

是根据下面的理论公式来的：

③.新函数array.T

import numpy as np

arr = np.arange(16).reshape(2, 2, 4)
print('arr:')
print(arr)

print('arr.transpose:')
print(arr.transpose())

print('arr.T:')
print(arr.T)

运行结果是：

arr:
[[[ 0  1  2  3]
  [ 4  5  6  7]]

 [[ 8  9 10 11]
  [12 13 14 15]]]
arr.transpose:
[[[ 0  8]
  [ 4 12]]

 [[ 1  9]
  [ 5 13]]

 [[ 2 10]
  [ 6 14]]

 [[ 3 11]
  [ 7 15]]]
arr.T:
[[[ 0  8]
  [ 4 12]]

 [[ 1  9]
  [ 5 13]]

 [[ 2 10]
  [ 6 14]]

 [[ 3 11]
  [ 7 15]]]

由此可见arr.T与arr.transpose函数实现的功能完全一致，均是实现矩阵的转置。
④.关于上下限H和L的取值：

                if (labelMat[i] != labelMat[j]):                              #L与H的求解公式请参照统计学习方法那两个图
                    L = max(0, alphas[j] - alphas[i])
                    H = min(C, C + alphas[j] - alphas[i])
                else:
                    L = max(0, alphas[j] + alphas[i] - C)
                    H = min(C, alphas[j] + alphas[i])

其理论依据为下面的推导：

3.测试其实际效果
为了测试简化版SMO算法的实际效果，我们运行如下命令：

dataMat , labelMat = loadDataSet('E:\学习资料\机器学习算法刻意练习\机器学习实战书电子版\machinelearninginaction\Ch06\\testSet.txt')
b,alphas = smoSimple(dataMat, labelMat,0.6,0.001,40)
print('b = ')
print(b)
print('alphas = ')
print(alphas)

运行后输出类似以下结果：

L==H
j not moving enough
L==H
j not moving enough
j not moving enough
...

b = 
[[-3.80125496]] 
alphas =
[[ 0.        ]
 [ 0.        ]
 [ 0.        ]
 ...
 [ 0.15960365]
 [ 0.        ]
 [ 0.        ]
 ...
 [ 0.        ]
 [ 0.        ]]

由于alphas矩阵中零元素过多，因此我们观察大于0的元素：

print('alphas = ',alphas[alphas>0])

结果如下：

alphas = [[ 0.14957524  0.16352387  0.04710753  0.36020665]]

注意：alphas[alphas>0]只对numpy类型的数组或者矩阵有用，不适用于python中的正则表。

二、利用完整Platt SMO算法加速优化

在简化版SMO算法的基础上作了以下改进：
①.选择alpha值的方式:
简化版SMO是在所有数据集上的单遍扫描；
Platt SMO算法的选择过程会在两种方式之间交替进行：
Ⅰ.在所有数据集上的单遍扫描
Ⅱ.在非边界alpha中单遍扫描
②.计算或者保存错误率的方式:
简化版SMO在选择第二个alpha后会计算Ej；
Platt SMO算法会建立一个全局的缓存来保存误差值，从中选择使步长Ei-Ej最大的alpha值。
1.几个辅助函数
①.定义了一个类optStruct，用来方便数据的存储和调用，与之前简化版所要实现的功能一模一样。

class optStruct:
    def __init__(self, dataMatIn, classLabels, C, toler):  # Initialize the structure with the parameters
        self.X = dataMatIn
        self.labelMat = classLabels
        self.C = C
        self.tol = toler
        self.m = np.shape(dataMatIn)[0]
        self.alphas = np.mat(np.zeros((self.m,1)))
        self.b = 0
        self.eCache = np.mat(np.zeros((self.m, 2)))  # first column is valid flag

由上可见，该类optStruct存储的内容有：数据集的特征矩阵，数据集的标签向量，C，数据集的个数m，常数项b和alpha等。

②.计算对输入的预测值与真实值之间的误差：

def calcEk(oS, k):#计算根据输入的预测值与真实值之间的差值
    fXk = float(np.multiply(oS.alphas, oS.labelMat).T * oS.K[:, k] + oS.b)
    Ek = fXk - float(oS.labelMat[k])
    return Ek

③.挑选第二个需要优化的alpha

def selectJ(i, oS, Ei):                                       #this is the second choice -heurstic, and calcs Ej
    maxK = -1
    maxDeltaE = 0                                             # 存储差值最大的两个E的差值
    Ej = 0
    oS.eCache[i] = [1, Ei]                                    #set valid #choose the alpha that gives the maximum delta E
    validEcacheList = np.nonzero(oS.eCache[:, 0].A)[0]        # 返回非零E值对应的alpha值
    if (len(validEcacheList)) > 1:                            # 如果不是第一次
        for k in validEcacheList:                             # 只遍历不在边界上的alpha并找出差值E最大的那个
            if k == i: continue                               # don't calc for i, waste of time
            Ek = calcEk(oS, k)                                # 计算根据输入的预测值与真实值之间的差值
            deltaE = abs(Ei - Ek)
            if (deltaE > maxDeltaE):                          # 找出两个alpha使其对应的E差值绝对值最大
                maxK = k
                maxDeltaE = deltaE
                Ej = Ek
        return maxK, Ej

    else:  # 第一次的话随机选一个
        j = selectJrand(i, oS.m)
        Ej = calcEk(oS, j)
    return j, Ej

注意：
Ⅰ.numpy下nonzero函数的作用：
首先我们随意些两个矩阵，注意一定要转换为矩阵形式，nonzero的对象不能是列表。

import numpy as np
data = [[1,2,5,6],
        [4,8,5,9],
        [8,7,4,2],
        [6,8,4,9],
        [8,2,1,6],
        [1,2,5,6],
        [4,8,5,9]]
index = [[1,55],
         [1,48],
         [2,59],
         [3,56],
         [2,74],
         [1,46],
         [3,99]]
data = np.mat(data)
index = np.mat(index)

之后执行下面命令print(index[:,0] == 1)，得到的结果是:

[[ True]
 [ True]
 [False]
 [False]
 [False]
 [ True]
 [False]]

可见输出是矩阵index所有行第0列元素是否等于1，等于取True，不等取Flase。
在此基础上看命令print(data[np.nonzero(index[:,0] == 1)])的效果：[[1 4 1]]，可知返回了data矩阵中的元素，其坐标与index中等于1的元素坐标相同。

Ⅱ.矩阵.A
功能：将矩阵转化为数组。

④.每次alpha变化后，更新全局存储的差值Ei:

def updateEk(oS, k):  # 每次alpha变化后，更新全局存储的差值Ei
    Ek = calcEk(oS, k)
    oS.eCache[k] = [1, Ek]

2.完整Platt SMO算法中的优化历程
之前我们完成了几个辅助函数，现在我们来看看更新后的主体函数。

def innerL(i, oS):
    Ei = calcEk(oS, i)
    if ((oS.labelMat[i]*Ei < -oS.tol) and (oS.alphas[i] < oS.C)) or ((oS.labelMat[i]*Ei > oS.tol) and (oS.alphas[i] > 0)):
        j, Ej = selectJ(i, oS, Ei) #this has been changed from selectJrand
        alphaIold = oS.alphas[i].copy()
        alphaJold = oS.alphas[j].copy()
        if oS.labelMat[i] != oS.labelMat[j]:
            L = max(0, oS.alphas[j] - oS.alphas[i])
            H = min(oS.C, oS.C + oS.alphas[j] - oS.alphas[i])
        else:
            L = max(0, oS.alphas[j] + oS.alphas[i] - oS.C)
            H = min(oS.C, oS.alphas[j] + oS.alphas[i])
        if L==H: print("L==H"); return 0
        eta = 2.0 * oS.K[i,j] - oS.K[i,i] - oS.K[j,j] #changed for kernel
        if eta >= 0: print("eta>=0"); return 0
        oS.alphas[j] -= oS.labelMat[j]*(Ei - Ej)/eta
        oS.alphas[j] = clipAlpha(oS.alphas[j],H,L)
        updateEk(oS, j) #added this for the Ecache
        if (abs(oS.alphas[j] - alphaJold) < 0.00001): print("j not moving enough"); return 0
        oS.alphas[i] += oS.labelMat[j]*oS.labelMat[i]*(alphaJold - oS.alphas[j])#update i by the same amount as j
        updateEk(oS, i) #added this for the Ecache                    #the update is in the oppostie direction
        b1 = oS.b - Ei- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,i] - oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[i,j]
        b2 = oS.b - Ej- oS.labelMat[i]*(oS.alphas[i]-alphaIold)*oS.K[i,j]- oS.labelMat[j]*(oS.alphas[j]-alphaJold)*oS.K[j,j]
        if (0 < oS.alphas[i]) and (oS.C > oS.alphas[i]): oS.b = b1
        elif (0 < oS.alphas[j]) and (oS.C > oS.alphas[j]): oS.b = b2
        else: oS.b = (b1 + b2)/2.0
        return 1
    else: return 0

从以上代码中我们可以看出，虽然有些细节上的实现改变了（例如：使用数据结构来存储和更新变量；挑选第二个alpha的方法变了），但是总体来讲与简化版SMO算法的smoSimple函数非常相似。

3.核函数kernel
前面介绍的普通的Platt SMO算法只能完成线性可分数据集的分类，然而很多数据集都是线性不可分的，这时候我们要实现对该种数据集的分类就要引入核函数kernel。
核函数可以将最原始的特征空间中的特征向量映射到更高维度的特征空间中，将原来线性不可分的数特征向量变成高维度特征空间中线性可分的特征向量，经过这种特征空间的变化后，我们解决了高维度特征空间中的线性可分就相当于解决了原始特征空间中的线性不可分问题。
下面我们介绍一种核函数：径向基函数，其公式如下图所示

基于该公式，我们易用代码来将其实现：

def kernelTrans(X, A, kTup): #calc the kernel or transform data to a higher dimensional space
    m,n = np.shape(X)
    K = np.mat(np.zeros((m,1)))
    if kTup[0]=='lin': K = X * A.T   #linear kernel
    elif kTup[0]=='rbf':
        for j in range(m):
            deltaRow = X[j,:] - A
            K[j] = deltaRow*deltaRow.T
        K = exp(K/(-1*kTup[1]**2)) #divide in NumPy is element-wise not matrix like Matlab
    else: raise NameError('Houston We Have a Problem -- \
    That Kernel is not recognized')
    return K

4.增加核函数后的类optStruct
因为我们在第三步中增加了核函数的实现，实现了从线性可分到线性不可分数据集分类的推广，所以我们也应该在最初定义的类optStruct中增加核函数的部分：

class optStruct:
    # def __init__(self, dataMatIn, classLabels, C, toler):  # Initialize the structure with the parameters
    def __init__(self, dataMatIn, classLabels, C, toler, kTup):
        self.X = dataMatIn
        self.labelMat = classLabels
        self.C = C
        self.tol = toler
        self.m = np.shape(dataMatIn)[0]
        self.alphas = np.mat(np.zeros((self.m,1)))
        self.b = 0
        self.eCache = np.mat(np.zeros((self.m, 2)))  # first column is valid flag
        self.K = np.mat(np.zeros((self.m, self.m)))
        for i in range(self.m):
            self.K[:, i] = kernelTrans(self.X, self.X[i, :], kTup)

5.完整版Platt SMO的外循环代码

def smoP(dataMatIn, classLabels, C, toler, maxIter,kTup=('lin', 0)):    #full Platt SMO
    oS = optStruct(np.mat(dataMatIn),np.mat(classLabels).transpose(),C,toler, kTup)
    iter = 0
    entireSet = True; alphaPairsChanged = 0
    while (iter < maxIter) and ((alphaPairsChanged > 0) or (entireSet)):#当迭代次数超过最大值，或者遍历整个集合都未对任何alpha做修改时就退出循环
        alphaPairsChanged = 0
        if entireSet:                                                   #遍历整个数据集
            for i in range(oS.m):
                alphaPairsChanged += innerL(i,oS)
                print("fullSet, iter: {} i:{}, pairs changed {}".format(iter,i,alphaPairsChanged))
            iter += 1
        else:                                                           #只遍历非边界的数据
            nonBoundIs = np.nonzero((oS.alphas.A > 0) * (oS.alphas.A < C))[0]
            for i in nonBoundIs:
                alphaPairsChanged += innerL(i,oS)                      #该语句与倒数第三四行的一起实现两种方式交叉遍历
                print("non-bound, iter: {} i:{}, pairs changed {}".format(iter,i,alphaPairsChanged))
            iter += 1
        if entireSet: entireSet = False 
        elif (alphaPairsChanged == 0): entireSet = True
        print("iteration number: {}".format(iter))
    return oS.b,oS.alphas

运行以下指令：

dataMat , labelMat = loadDataSet('E:\学习资料\机器学习算法刻意练习\机器学习实战书电子版\machinelearninginaction\Ch06\\testSet.txt')
b,alphas = smoP(dataMat, labelMat,0.6,0.001,40)
print(b,alphas)

运行结果与简化版SMO类似（运行速度会变快，而且可以用于线性不可分数据集）：

...
j not moving enough
fullSet, iter: 2 i:97, pairs changed 0
fullSet, iter: 2 i:98, pairs changed 0
fullSet, iter: 2 i:99, pairs changed 0
iteration number: 3
[[-2.89901748]] 
[[ 0.06961952]
 [ 0.        ]
 [ 0.        ]
 [ 0.0169055 ]
 [ 0.0169055 ]
 [ 0.        ]
 ...
 [ 0.        ]
 [ 0.        ]
 [ 0.        ]]

小结：
本算法为整个机器学习中最基础也是最重要的算法之一。其实现运用了很多理论方面的基础知识，还通过灵活运用矩阵及其转置完成向量的操作。
最重要的是引入核函数kernel之后，将适用范围扩展到了非线性可分的数据集的分类问题。核函数在处理非线性可分的原始数据中起到了至关重要的作用，之后应结合理论推导再次温习SVM与kernel。