机器学习笔记之变分自编码器(一)模型表示
机器学习笔记之变分自编码器——模型表示
- 引言
-
- 回顾:高斯混合模型
- 变分自编码器——概率图视角介绍
- 总结
引言
本节将介绍变分自编码器(Variational AutoEncoder,VAE)。
回顾:高斯混合模型
高斯混合模型本质上是 K \mathcal K K个高斯分布的混合分布。它的概率图结构表示如下:
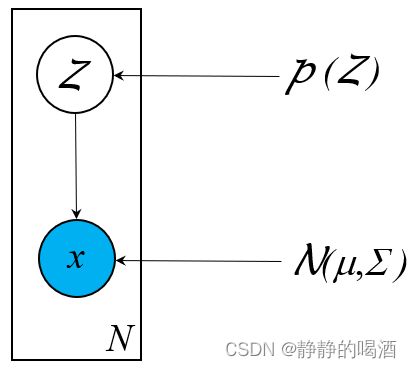
其中 Z \mathcal Z Z是一个离散型随机变量,一共包含 K \mathcal K K种选择结果(服从 Categorical \text{Categorical} Categorical分布);并且隐变量 Z \mathcal Z Z的每个取值 z j ∈ Z z_j \in \mathcal Z zj∈Z均唯一对应一个高斯分布 N ( μ j , Σ j ) \mathcal N(\mu_j,\Sigma_j) N(μj,Σj):
并满足 ∑ k = 1 K = 1 \sum_{k=1}^{\mathcal K} = 1 ∑k=1K=1.
| Z \mathcal Z Z | z 1 z_1 z1 | z 2 z_2 z2 | ⋯ \cdots ⋯ | z K z_{\mathcal K} zK |
|---|---|---|---|---|
| P ( Z ) \mathcal P(\mathcal Z) P(Z) | p 1 p_1 p1 | p 2 p_2 p2 | ⋯ \cdots ⋯ | p K p_{\mathcal K} pK |
| P ( x ∣ Z ) \mathcal P(x \mid \mathcal Z) P(x∣Z) | N ( μ 1 , Σ 1 ) \mathcal N(\mu_1,\Sigma_1) N(μ1,Σ1) | N ( μ 2 , Σ 2 ) \mathcal N(\mu_2,\Sigma_2) N(μ2,Σ2) | ⋯ \cdots ⋯ | N ( μ K , Σ K ) \mathcal N(\mu_{\mathcal K},\Sigma_{\mathcal K}) N(μK,ΣK) |
变分自编码器——概率图视角介绍
从模型名称观察:
- 变分自编码器中的变分自然是指变分推断(Variational Inference,VI);这个概念来自于概率图模型对变量(隐变量)的条件概率进行求解。
- 变分自编码器中的自编码器(AutoEncoder,AE)来自于前馈神经网络结构。不同于概率图模型,它是一种计算图结构;并且它的底层逻辑是通用逼近定理,通过各网络层的参数对概率分布进行表达。
因此,变分自编码器是一种典型的:
- 概率图、计算图相结合的模型;
- 它也是一个隐变量模型(Latent Variable Model,LVM)。它的概率图结构表示如下:
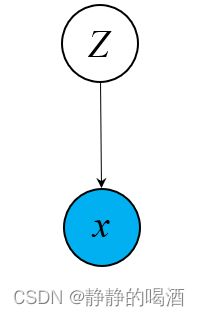
- 它也是一个静态模型(Static Model)。
这里主要是区别于‘隐马尔可夫模型’系列的动态模型(Dynamic Model)。
在之前的介绍中,提到过一种简单的静态隐变量模型——高斯混合模型(Gaussian Mixture Model,GMM),观察高斯混合模型与变分自编码器之间的关联关系。
如果从若干个高斯分布混合的角度观察高斯混合模型,那么变分自编码器可看作 无限个高斯分布混合。在高斯混合模型中,隐变量 Z \mathcal Z Z被假设为 1 1 1维、服从 Categorical \text{Categorical} Categorical分布的离散型随机变量。
而高斯混合模型常用于处理无监督的聚类任务。换句话说,因为隐变量 Z \mathcal Z Z的假设,或者说它的复杂程度过于简单,使得高斯混合模型只能处理 浅层特征。相反,如果给定一张图片,去执行图像识别或者是目标检测, GMM \text{GMM} GMM显然是无法实现的。
如何从探索深层特征?这需要提高隐变量 Z \mathcal Z Z的复杂程度:
- (特征维度角度的扩展) Z \mathcal Z Z: 1 1 1维特征 ⇒ \Rightarrow ⇒ 高维特征;
需要注意的是,这里的下标表示随机变量的维度下标,不同于上面的取值下标,M \mathcal M M表示维度数量。
Z = ( z 1 , z 2 , ⋯ , z M ) T \mathcal Z = (z_1,z_2,\cdots,z_{\mathcal M})^T Z=(z1,z2,⋯,zM)T - (随机变量性质角度的扩展) Z \mathcal Z Z:离散型随机变量 ⇒ \Rightarrow ⇒ 连续型随机变量。
这里不妨假设 Z \mathcal Z Z服从高斯分布:
均值为0,协方差矩阵为标准单位矩阵 I M × M \mathcal I_{\mathcal M \times \mathcal M} IM×M.
Z ∼ N ( 0 , I M × M ) \mathcal Z \sim \mathcal N(0,\mathcal I_{\mathcal M \times \mathcal M}) Z∼N(0,IM×M)
在给定隐变量 Z \mathcal Z Z的条件下,样本 x x x的后验分布 x ∣ Z x \mid \mathcal Z x∣Z可分为两种情况:
这里仅对 x x x是连续型随机变量进行讨论。
- 如果 x x x是离散型随机变量,那么 x x x将服从 Categorical \text{Categorical} Categorical分布或者是伯努利分布(视情况而定);
这里需要注意的是,这个Categorical \text{Categorical} Categorical分布是针对x x x的,区别于高斯混合模型中针对Z \mathcal Z Z的分布。 - 如果 x x x是连续型随机变量,那么通常将 x x x服从高斯分布:
注意:这里将高斯分布的期望、协方差μ , Σ \mu,\Sigma μ,Σ描述成关于'给定条件'Z \mathcal Z Z的函数,函数对应的权重参数设置为θ \theta θ.设置成μ ( Z ; θ ) , Σ ( Z ; θ ) \mu(\mathcal Z;\theta),\Sigma(\mathcal Z;\theta) μ(Z;θ),Σ(Z;θ)的目的是使用神经网络的‘通用逼近定理’去近似学习θ \theta θ,从而得到μ , Σ \mu,\Sigma μ,Σ的近似解。
x ∣ Z ∼ N [ μ ( Z ; θ ) , Σ ( Z ; θ ) ] x \mid \mathcal Z \sim \mathcal N\left[\mu(\mathcal Z;\theta),\Sigma(\mathcal Z;\theta)\right] x∣Z∼N[μ(Z;θ),Σ(Z;θ)]
之所以使用神经网络来学习权重参数 θ \theta θ表示 μ ( Z ; θ ) , Σ ( Z ; θ ) \mu(\mathcal Z;\theta),\Sigma(\mathcal Z;\theta) μ(Z;θ),Σ(Z;θ),是因为隐变量 Z \mathcal Z Z可能维度/复杂程度极高,即便使用重参数化技巧来近似求解分布也是极为复杂的。
以随机梯度变分推断为例,关于假定分布Q ( Z ) \mathcal Q(\mathcal Z) Q(Z)的变分L [ Q ( Z ) ] \mathcal L[\mathcal Q(\mathcal Z)] L[Q(Z)]可表示为关于参数ϕ \phi ϕ的函数形式:(这里将假定分布Q ( Z ) \mathcal Q(\mathcal Z) Q(Z)看做一个关于ϕ \phi ϕ的函数),推导过程详见随机梯度变分推断( SGVI \text{SGVI} SGVI)
这里的X \mathcal X X指观测变量(样本)的随机变量集合。
L [ Q ( Z ) ] = E Q ( Z ; ϕ ) [ log P ( X , Z ) − log Q ( Z ; ϕ ) ] ⏟ ELBO = L ( ϕ ) \begin{aligned} \mathcal L[\mathcal Q(\mathcal Z)] & = \underbrace{\mathbb E_{\mathcal Q(\mathcal Z ; \phi)} \left[\log \mathcal P(\mathcal X,\mathcal Z) - \log \mathcal Q(\mathcal Z;\phi)\right]}_{\text{ELBO}} = \mathcal L(\phi)\\ \end{aligned} L[Q(Z)]=ELBO EQ(Z;ϕ)[logP(X,Z)−logQ(Z;ϕ)]=L(ϕ)而变分关于ϕ \phi ϕ的梯度∇ ϕ L ( ϕ ) \nabla_{\phi}\mathcal L(\phi) ∇ϕL(ϕ)最终可以表示成期望形式:
∇ ϕ L ( ϕ ) = E Q ( Z ; ϕ ) { ∇ ϕ log Q ( Z ; ϕ ) ⋅ [ log P ( X , Z ) − log Q ( Z ; ϕ ) ] } \nabla_{\phi}\mathcal L(\phi) = \mathbb E_{\mathcal Q(\mathcal Z;\phi)} \left\{\nabla_{\phi}\log \mathcal Q(\mathcal Z;\phi) \cdot \left[\log \mathcal P(\mathcal X,\mathcal Z) - \log \mathcal Q(\mathcal Z;\phi)\right]\right\} ∇ϕL(ϕ)=EQ(Z;ϕ){∇ϕlogQ(Z;ϕ)⋅[logP(X,Z)−logQ(Z;ϕ)]}
而在使用‘蒙特卡洛方法’近似过程中,首先针对∇ ϕ L ( ϕ ) \nabla_{\phi}\mathcal L(\phi) ∇ϕL(ϕ)的近似需要采集大量样本,其次也会出现高方差的现象。虽然使用‘重参数化技巧’能够有效减小高方差的现象,但本质依然需要大量采样:
Z = G ( ϵ , X ; ϕ ) ∇ ϕ L ( ϕ ) = E P ( ϵ ) [ ∇ Z [ log P ( X , Z ) − log Q ( Z ; ϕ ) ] ⋅ ∇ ϕ G ( ϵ , X ; ϕ ) ] \mathcal Z = \mathcal G(\epsilon,\mathcal X ;\phi) \\ \nabla_{\phi}\mathcal L(\phi) = \mathbb E_{\mathcal P(\epsilon)} \left[\nabla_{\mathcal Z} \left[\log \mathcal P(\mathcal X,\mathcal Z) - \log \mathcal Q(\mathcal Z;\phi)\right] \cdot \nabla_{\phi} \mathcal G(\epsilon,\mathcal X;\phi)\right] Z=G(ϵ,X;ϕ)∇ϕL(ϕ)=EP(ϵ)[∇Z[logP(X,Z)−logQ(Z;ϕ)]⋅∇ϕG(ϵ,X;ϕ)]
如果Z \mathcal Z Z维度足够高,那么意味着假定分布Q ( Z ) \mathcal Q(\mathcal Z) Q(Z)足够复杂,因而需要采集足够的样本去近似∇ ϕ L ( ϕ ) \nabla_{\phi}\mathcal L(\phi) ∇ϕL(ϕ),这仅是梯度上升的一次迭代,计算代价是极高的。
如果使用 x ∣ Z ∼ N [ μ ( Z ; θ ) , Σ ( Z ; θ ) ] x \mid \mathcal Z \sim \mathcal N\left[\mu(\mathcal Z;\theta),\Sigma(\mathcal Z;\theta)\right] x∣Z∼N[μ(Z;θ),Σ(Z;θ)]这种假设,那么关于观测变量集合 X \mathcal X X的边缘概率分布可表示为:
其中P ( Z ) \mathcal P(\mathcal Z) P(Z)指隐变量Z \mathcal Z Z的先验概率:Z ∼ N ( 0 , I M × M ) \mathcal Z \sim \mathcal N(0,\mathcal I_{\mathcal M \times \mathcal M}) Z∼N(0,IM×M),但在前馈神经网络结构的学习过程中,Z \mathcal Z Z的先验分布显得并不重要。和生成对抗网络(GAN)中关于生成模型中的输入一样,它就仅是满足“高维、连续”条件的一个简单分布。相比于先验分布P ( Z ) \mathcal P(\mathcal Z) P(Z),我们实际上更关心'后验概率'P ( Z ∣ X ) \mathcal P(\mathcal Z \mid \mathcal X) P(Z∣X),即通过样本的学习出的隐变量的分布信息。

但变分自编码器中关于噪声部分的输出是高斯分布,这里只是假定x ∣ Z x \mid \mathcal Z x∣Z服从高斯分布N [ μ ( Z ; θ ) , Σ ( Z ; θ ) ] \mathcal N\left[\mu(\mathcal Z;\theta),\Sigma(\mathcal Z;\theta)\right] N[μ(Z;θ),Σ(Z;θ)],但它实际上可能是任意分布。但有神经网络的通用逼近定理,不需要担心,它仅是使用一个简单高斯分布N ( 0 , I M × M ) \mathcal N(0,\mathcal I_{\mathcal M \times \mathcal M}) N(0,IM×M)作为输入,通过模型参数逼近真实的噪声分布(见图)。
P ( X ) = ∫ Z P ( X , Z ) d Z = ∫ Z P ( Z ) ⏟ Prior ⋅ P ( X ∣ Z ) d Z { Z ∼ N ( 0 , I M × M ) X ∣ Z ∼ N [ μ ( Z ; θ ) , Σ ( Z ; θ ) ] \begin{aligned} \mathcal P(\mathcal X) & = \int_{\mathcal Z} \mathcal P(\mathcal X,\mathcal Z) d\mathcal Z \\ & = \int_{\mathcal Z} \underbrace{\mathcal P(\mathcal Z)}_{\text{Prior}} \cdot \mathcal P(\mathcal X \mid \mathcal Z) d\mathcal Z \quad \begin{cases} \mathcal Z \sim \mathcal N(0,\mathcal I_{\mathcal M \times \mathcal M}) \\ \mathcal X \mid \mathcal Z \sim \mathcal N \left[\mu(\mathcal Z;\theta),\Sigma(\mathcal Z;\theta)\right] \end{cases} \end{aligned} P(X)=∫ZP(X,Z)dZ=∫ZPrior P(Z)⋅P(X∣Z)dZ{Z∼N(0,IM×M)X∣Z∼N[μ(Z;θ),Σ(Z;θ)]
如果基于上述假设,此时隐变量 Z \mathcal Z Z的维度极高( M \mathcal M M),这导致 ∫ Z \int_{\mathcal Z} ∫Z是极复杂的,甚至是 无法处理的( Intractable \text{Intractable} Intractable)。这导致 P ( X ) \mathcal P(\mathcal X) P(X)也是无法直接求解的:
P ( X ) ⏟ Intractable = ∫ Z [ P ( Z 1 , ⋯ , Z M ) ⋅ P ( X ∣ Z 1 , ⋯ Z M ) ] d Z 1 , ⋯ Z Z M = ∫ Z 1 ∫ Z 2 ⋯ ∫ Z M [ P ( Z 1 , ⋯ , Z M ) ⋅ P ( X ∣ Z 1 , ⋯ Z M ) ] d Z 1 , ⋯ Z Z M \begin{aligned} \underbrace{\mathcal P(\mathcal X) }_{\text{Intractable}} & = \int_{\mathcal Z} \left[\mathcal P(\mathcal Z_1,\cdots,\mathcal Z_{\mathcal M}) \cdot \mathcal P(\mathcal X \mid \mathcal Z_1,\cdots \mathcal Z_{\mathcal M})\right] d\mathcal Z_1,\cdots \mathcal Z_{\mathcal Z_{\mathcal M}} \\ & = \int_{\mathcal Z_1}\int_{\mathcal Z_2}\cdots \int_{\mathcal Z_{\mathcal M}} \left[\mathcal P(\mathcal Z_1,\cdots,\mathcal Z_{\mathcal M}) \cdot \mathcal P(\mathcal X \mid \mathcal Z_1,\cdots \mathcal Z_{\mathcal M})\right] d\mathcal Z_1,\cdots \mathcal Z_{\mathcal Z_{\mathcal M}} \end{aligned} Intractable P(X)=∫Z[P(Z1,⋯,ZM)⋅P(X∣Z1,⋯ZM)]dZ1,⋯ZZM=∫Z1∫Z2⋯∫ZM[P(Z1,⋯,ZM)⋅P(X∣Z1,⋯ZM)]dZ1,⋯ZZM
根据贝叶斯定理,关于隐变量的后验分布 P ( Z ∣ X ) \mathcal P(\mathcal Z \mid \mathcal X) P(Z∣X)同样是无法处理的( Intractable \text{Intractable} Intractable):
也就是贝叶斯定理自身的‘积分难问题’。
P ( Z ∣ X ) ⏟ Intractable = P ( X , Z ) P ( X ) = P ( Z ) ⋅ P ( X ∣ Z ) P ( X ) \underbrace{\mathcal P(\mathcal Z \mid \mathcal X)}_{\text{Intractable}} = \frac{\mathcal P(\mathcal X,\mathcal Z)}{\mathcal P(\mathcal X)} = \frac{\mathcal P(\mathcal Z) \cdot \mathcal P(\mathcal X \mid \mathcal Z)}{\mathcal P(\mathcal X)} Intractable P(Z∣X)=P(X)P(X,Z)=P(X)P(Z)⋅P(X∣Z)
总结
从概率图视角观察,变分自编码器就是一个隐变量模型( Latent Variable Model \text{Latent Variable Model} Latent Variable Model),相比于高斯混合模型的建模思路,变分自编码器的特点是隐变量 Z \mathcal Z Z足够复杂—— Z \mathcal Z Z被假设为高维、连续的随机变量。
这里仅将 P ( Z ) \mathcal P(\mathcal Z) P(Z)设置成一个满足高维、连续的简单分布:
Z ∼ N ( 0 , I M × M ) \mathcal Z \sim \mathcal N(0,\mathcal I_{\mathcal M \times \mathcal M}) Z∼N(0,IM×M)
因为隐变量 Z \mathcal Z Z是建模过程中假设的变量,在没有真实样本 X \mathcal X X的条件下,先验分布 P ( Z ) \mathcal P(\mathcal Z) P(Z)并不重要。在极大似然估计与最大后验概率估计一节中介绍过,当真实样本足够多的时候,先验概率的权重会逐渐缩减。而生成过程 P ( X ∣ Z ) \mathcal P(\mathcal X \mid \mathcal Z) P(X∣Z)的概率分布通常设置为如下形式:
X ∣ Z ∼ N [ μ ( Z ; θ ) , Σ ( Z ; θ ) ] \mathcal X \mid \mathcal Z \sim \mathcal N \left[\mu(\mathcal Z ;\theta),\Sigma(\mathcal Z;\theta)\right] X∣Z∼N[μ(Z;θ),Σ(Z;θ)]
需要注意的是,虽然这里写成了高斯分布的格式,但实际上它可能是任意噪声分布。由于 Z \mathcal Z Z维度可能过于复杂,仅通过蒙特卡洛方法采样(随机梯度变分推断( SGVI \text{SGVI} SGVI),重参数化技巧等)计算代价极高。因此使用神经网络,调整参数 θ \theta θ,使 N [ μ ( Z ; θ ) , Σ ( Z ; θ ) ] \mathcal N \left[\mu(\mathcal Z ;\theta),\Sigma(\mathcal Z;\theta)\right] N[μ(Z;θ),Σ(Z;θ)]逼近任意噪声分布。
相比之下,我们更关心隐变量的后验分布 P ( Z ∣ X ; θ ) \mathcal P(\mathcal Z \mid \mathcal X;\theta) P(Z∣X;θ)。因为此时的隐变量分布在真实样本的加持下,具有了实际意义。但根据贝叶斯定理, P ( Z ∣ X ; θ ) \mathcal P(\mathcal Z \mid \mathcal X;\theta) P(Z∣X;θ)同样存在积分难问题:
这里的 P ( Z ) \mathcal P(\mathcal Z) P(Z)与对应的 P ( Z 1 , ⋯ Z M ) \mathcal P(\mathcal Z_1,\cdots \mathcal Z_{\mathcal M}) P(Z1,⋯ZM)均指的使先验分布,它们作为神经网络的输入,并不会更新自身梯度。因此这里没有加 θ \theta θ.
P ( Z ∣ X ; θ ) ⏟ Intractable = P ( Z ) ⋅ P ( X ∣ Z ; θ ) P ( X ; θ ) ⏟ Intractable { Z ∼ N ( 0 , I M × M ) X ∣ Z ∼ N [ μ ( Z ; θ ) , Σ ( Z ; θ ) ] P ( X ; θ ) = ∫ Z 1 ⋯ ∫ Z M [ P ( Z 1 , ⋯ , Z M ) ⋅ P ( X ∣ Z 1 , ⋯ Z M ; θ ) ] d Z 1 , ⋯ Z M \begin{aligned} \underbrace{\mathcal P(\mathcal Z \mid \mathcal X;\theta)}_{\text{Intractable}} & = \frac{\mathcal P(\mathcal Z) \cdot \mathcal P(\mathcal X \mid \mathcal Z;\theta)}{\underbrace{\mathcal P(\mathcal X;\theta)}_{\text{Intractable}}} \quad \begin{cases} \mathcal Z \sim \mathcal N(0,\mathcal I_{\mathcal M \times \mathcal M}) \\ \mathcal X \mid \mathcal Z \sim \mathcal N \left[\mu(\mathcal Z ;\theta),\Sigma(\mathcal Z;\theta)\right] \end{cases} \\ \mathcal P(\mathcal X;\theta) & = \int_{\mathcal Z_1}\cdots \int_{\mathcal Z_{\mathcal M}} \left[\mathcal P(\mathcal Z_1,\cdots,\mathcal Z_{\mathcal M}) \cdot \mathcal P(\mathcal X \mid \mathcal Z_1,\cdots \mathcal Z_{\mathcal M};\theta) \right] d\mathcal Z_1,\cdots \mathcal Z_{\mathcal M} \end{aligned} Intractable P(Z∣X;θ)P(X;θ)=Intractable P(X;θ)P(Z)⋅P(X∣Z;θ){Z∼N(0,IM×M)X∣Z∼N[μ(Z;θ),Σ(Z;θ)]=∫Z1⋯∫ZM[P(Z1,⋯,ZM)⋅P(X∣Z1,⋯ZM;θ)]dZ1,⋯ZM
因此需要使用推断的方式将 P ( Z ∣ X ) \mathcal P(\mathcal Z \mid \mathcal X) P(Z∣X)求解出来,从而实现样本的生成过程。
下一节将介绍变分自编码器的推断过程。
相关参考:
变分自编码器——模型表示