深度学习笔记之稀疏自编码器

引言

本节以一道算法八股题为引，介绍稀疏自编码器。

引子：题目描述

下列方法中，可以用于特征降维的方法包括(多选)$()$

$\mathcal{A}$主成分分析$\text{PCA}$

$\mathcal{B}$线性判别分析$\text{LDA}$

$\mathcal{C}$深度学习$\text{SparseAutoEncoder}$

$\mathcal{D}$矩阵奇异值分解$\text{SVD}$

$\mathcal{E}$最小二乘法$\text{LeastSquares}$

正确答案：$\mathcal{A}\mathcal{BC}\mathcal{D}$

题目解析

关于 $\mathcal{A}\mathcal{D}$ 选项，可以放在一起观察。关于主成分分析$(\text{Principal Component Analysis,PCA})$的降维思想，这里不再过多赘述。这里重点描述从奇异值分解角度观察主成分分析：
详细推导过程见传送门

• 假设无监督任务下，样本集合$\mathcal{X}$表示为：
  $$\mathcal{X}=(x^{(1)},x^{(2)},\cdots ,x^{(N)}{)}_{N\times p}^T{x}^{(i)}\in {\mathbb{R}}^p$$
• 对$\mathcal{X}$进行中心化(将$\mathcal{X}$分布平移至样本空间原点位置)，即乘以相应的中心矩阵$\mathcal{H}$：
  其中${\mathcal{E}}_N$表示$N$维单位向量;${\mathcal{I}}_N$表示元素值均为$1$的$N$维列向量。
  $$\{\begin{array}{l}\begin{array}{r}\mathcal{H}={\mathcal{E}}_N-\frac{1}{N}{\mathcal{I}}_N\cdot {\mathcal{I}}_N^T\end{array}\\ \mathcal{H}\cdot \mathcal{X}={\left[x^{(1)}-\bar{\mathcal{X}},x^{(2)}-\bar{\mathcal{X}},\cdots ,x^{(N)}-\bar{\mathcal{X}}\right]}_{N\times p}^T\end{array}$$
  从奇异值分解$(\text{Singular Value Decomposition,SVD})$的角度对$\mathcal{H}\cdot \mathcal{X}$进行处理：
  $$\mathcal{H}\cdot \mathcal{X}=\mathcal{U}\Sigma {\mathcal{V}}^T$$
  其中$\mathcal{U}$是列正交矩阵；$\mathcal{V}$是正交矩阵。对应$\mathcal{X}$的协方差$\mathcal{S}$使用奇异值分解表示如下：
  其中$\mathcal{X},\mathcal{H}$对$\mathcal{S}$的表达过程详见主成分分析——最大投影方差角度
  $$\begin{array}{rl}\mathcal{S}& =\frac{1}{N}{\mathcal{X}}^T\cdot \mathcal{H}\cdot \mathcal{X}\\ & =\frac{1}{N}(\mathcal{H}\mathcal{X}{)}^T\cdot (\mathcal{H}\mathcal{X})\\ & =\frac{1}{N}(\mathcal{U}\Sigma {\mathcal{V}}^T{)}^T\cdot \mathcal{U}\Sigma {\mathcal{V}}^T\\ & =\frac{1}{N}\mathcal{V}({\Sigma }^T\Sigma ){\mathcal{V}}^T\end{array}$$
  这里忽略掉$\begin{array}{r}\frac{1}{N}\end{array}$的影响(它不会影响正交基的方向)，这意味着不需要直接对$\mathcal{X}$的协方差矩阵进行特征值分解，而是通过$\mathcal{H}\cdot \mathcal{X}$进行奇异值分解即可。其特征向量就是$\mathcal{V}$自身：
  上式等号两侧右乘$\mathcal{V},\begin{array}{r}\frac{1}{N}\end{array}$忽略。
  $$\begin{array}{rl}\mathcal{S}\cdot \mathcal{V}& =\mathcal{V}{\Sigma }^T\Sigma \underset{\mathcal{E}}{{\mathcal{V}}^T\mathcal{V}}\\ & =\mathcal{V}({\Sigma }^T\Sigma )\end{array}$$
  其中${\Sigma }^T\Sigma$是特征值矩阵，其对角线元素是特征值，从而根据特征值进行找出最优主成分，以此类推。因此，$\mathcal{D}$ 选项正确。

关于 $\mathcal{B}$ 选项：线性判别分析，这里不过多赘述，详见算法八股(十)——线性判别分析与核函数中关于线性判别分析的解释。
关于 $\mathcal{E}$ 选项：最小二乘法：
$$\mathcal{L}(\mathcal{W})=\sum _{i=1}^N||{\mathcal{W}}^T{x}^{(i)}-y^{(i)}||(x^{(i)},y^{(i)})\in \mathcal{D}$$
我们仅从计算过程中观察，我们可以认为将$x^{(i)}$所在的特征空间通过$\mathcal{W}$映射到对应的标签空间。但整个过程$x^{(i)}(i=1,2,\cdots ,N)$的特征没有变化过。也就是说，我们并没有去修改特征空间，从而对$x^{(i)}$提出新的表示。

下面主要关注 $\mathcal{C}$ 选项：什么是稀疏自编码器($\text{SparseAutoEncoder}$)，它又是如何实现特征降维的。

介绍：自编码器

关于自编码器$(\text{AutoEncoder})$，是神经网络的一种。它经过训练后能尝试将输入复制到输出。其模型结构可表示为如下形式：
节自《深度学习》(花书) P306。从该描述中可以发现，它是一个典型的概率生成模型

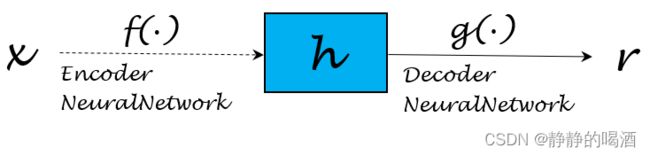
该模型中包含一个隐藏层$h$，其作用是对输入特征$x$进行抽象表示，也称作编码$(\text{Code})$。通过$h$将整个模型划分成两个部分：

• 编码器$(\text{Encoder})$。由函数$f(\cdot )$对输入特征$x$进行描述，得到抽象特征$h$：
  $$h=f(x)$$
• 解码器$(\text{Decoder})$。由函数$g(\cdot )$对抽象特征$h$进行重构，得到生成特征$r$：
  $$r=g(h)$$

既然是生成模型，从常规角度认为从模型中生成出的特征$r$和$x$越相似越好。但相反，如果仅仅得到一个$g[f(x)]=x$，这个模型可能并没有什么意义。因此，我们需要对模型施加一些约束，从而：

• 生成的特征和输入特征相似；
• 施加的约束导致模型会优先选择代表性强的特征，从而学习到数据的有用特征。

如果从概率分布的角度认识这个过程，已知输入分布$x$，那么编码器的输出分布可表示为：
也就是给定$x$,在$\text{Encoder}$的抽象描述下，输出编码$h$的后验概率分布。
$${\mathcal{P}}_{encoder}(h\mid x)$$
同理，假设编码$h$给定的条件下，解码器的输出分布可表示为：
$${\mathcal{P}}_{decoder}(x\mid h)$$

欠完备自编码器

基于我们想要输出分布${\mathcal{P}}_{model}(x\mid h)$与真实分布${\mathcal{P}}_{data}(x)$相同，但又不想单纯地将输入复制到输出。
看起来像是一个矛盾的事情。

也就是说，在训练自编码器对$x$训练的过程中，使隐变量$h$能够学习到有用的特性。一种做法是：通过人工设置，强行让$h$的维度小于$x$的维度：

这种编码维度小于输入维度的自编码器被称作欠完备自编码器$(\text{Undercompleter AutoEncoder})$。编码维度的减小意味着学习到的分布${\mathcal{P}}_{model}(h\mid x)$相比真实分布${\mathcal{P}}_{data}(x)$确实出现了缺失，但强制自编码器捕捉$x$中最显著的特征。
从$x\Rightarrow h$过程中学习到的特征信息被‘压缩’，信息丢失是不可避免的。但在$x$分布确定的条件下，$h$中保留的必然是‘更具代表性、性质更加显著’的信息。

在后续解码器对压缩特征$h$进行重构的过程中，由于$h$特征的缺失已经达到了 不想单纯地将输入复制到输出 这个动机，导致后续即便重构出与$x$大小相同的特征空间，它的信息相比真实分布$x$依然是缺失的。因而我们需要一个损失函数来惩罚重构分布和真实分布 之间的差异：
$$\mathcal{L}[x,g(f(x))]$$
从降维的角度观察，$x\Rightarrow h$可以被看作是一个降维过程，$h$中的各维度可看作特征值最大的若干主成分。在重构过程中，虽然无法将缺失的部分还原，但重构后的结果相比于真实分布其特征更具代表性。
也就是说，$\text{Undercompleter AutoEncoder}$这种独特的模型结构就已经存在了特征降维的思想。那么它与$\text{Sparse AutoEncdoer}$之间的关联关系是什么？

正则自编码器

上面描述的欠完备自编码器是通过人为设置强制减小编码维数而产生的模型结构，这种结构能够使$h$学习到$x$更显著的特征信息。

相反呢？如果我们的自编码器容量过大，也就是说：$h$的编码维数与$x$相等，甚至高于$x$：

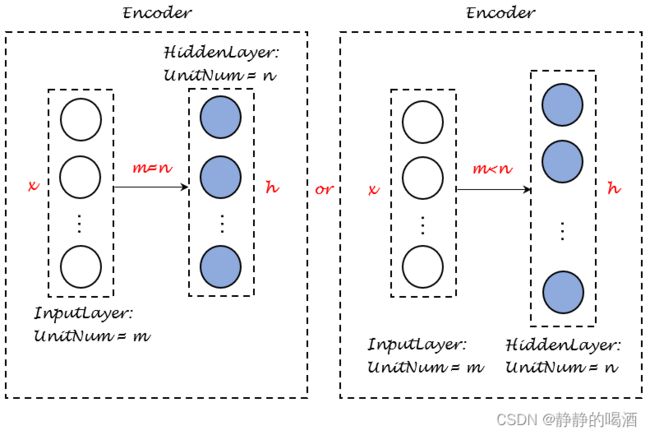
这种情况可能导致$h$在编码过程中对$x$的学习更加准确，我们不否认对应的解码结果会对$x$重构的更加准确，但$h$中学习不到任何有用的信息。
这种就是‘单纯地将输入复制到输出’的情况。

我们将这种情况称作过完备$(\text{Overcomplete})$。那么类似于上述的情况，是否可以让$h$学习到有用的信息？换句话说：能否不使用“限制”$h$维度的方式，理想情况下，任意大小的$h$都能够在训练中学习出有用的信息。

正则自编码器提供了这样的能力。其思想在于利用稀疏表示、表示的小导数以及噪声或输入缺失的鲁棒性的方式，使非线性且过完备的正则自编码器仍然能够从数据中学到一些关于数据分布的有用信息。
节自《深度学习》(花书) P307 14.2 正则自编码器

从先验角度解释稀疏自编码器

稀疏自编码器$(\text{Sparse AutoEncoder})$就是通过对$h$进行稀疏表示达到上述目的。其具体做法是：在损失函数的基础上，增加对$h$的稀疏惩罚：
再次强调，两个部分‘惩罚’的方向不一样。$\mathcal{L}[x,g(f(x))]$惩罚的是真实分布$x$和重构分布$g(f(x))$之间的差异性;$\Omega (h)$惩罚的是$h=f(x)$的稀疏性。
$$\mathcal{L}[x,g(f(x))]+\Omega (h)h=f(x)$$

我们可以将$\Omega (h)$视作关于$h$的正则项，但实际上，该项并没有正则项的意义。在正则化——贝叶斯概率角度中介绍了正则项相当于参数的先验概率：
$$\text{MAP : }\hat{\theta }=\mathrm{argmax}\theta \left[\log \mathcal{P}(\mathcal{X}\mid \theta )+\log \mathcal{P}(\theta )\right]$$
而先验概率$\log \mathcal{P}(\theta )$描述在训练过程之前，对参数$\theta$特定值的偏好，并且 这个偏好取决于事件自身的性质。例如极大似然估计与最大后验概率估计中投掷硬币的例子。我们给出的分布$\mathcal{P}(\theta )$是均值$\mu =0.5$，方差$\sigma =0.1$的高斯分布：
很明显，我们在给出先验分布时，连数据是什么都不知道。
$$\mathcal{P}(\theta )=\frac{1}{0.1\times \sqrt{2\pi }}\exp \left\{-\frac{(\theta -0.5{)}^2}{0.02}\right\}$$
但是隐变量$h$是伴随模型存在的，它自身没有实际的物理意义。因而对应的先验分布${\mathcal{P}}_{model}(h)$也同样是没有实际意义的先验。因而它不能被直接视作正则项，但我们仍可以认为${\mathcal{P}}_{model}(h)$隐式地表达了对函数的偏好：
通常也将${\mathcal{P}}_{model}(h)$称作信念先验。节选自《深度学习》(花书) P308 14.2.1 稀疏自编码器。

关于解码器生成的样本分布${\mathcal{P}}_{model}(x)$，它的似然函数可分解为如下形式：
$${\mathcal{P}}_{model}(x)=\sum _h{\mathcal{P}}_{model}(h,x)$$
关于联合概率分布${\mathcal{P}}_{model}(h,x)$，它的对数结果表示为：
$$\begin{array}{rl}\log {\mathcal{P}}_{model}(h,x)& =\log \left[{\mathcal{P}}_{model}(x\mid h)\cdot {\mathcal{P}}_{model}(h)\right]\\ & =\log {\mathcal{P}}_{model}(x\mid h)+\log {\mathcal{P}}_{model}(h)\end{array}$$
如果$h$，也就是编码器各神经元的输出，假设它们之间是独立同分布的条件下，虽然${\mathcal{P}}_{model}(h)$不是真正意义上的先验，但是依然可以给其各个分量一个先验分布。如$\text{Laplace}$先验：
其中$h_j(j=1,2,\cdots ,\mathcal{K})$表示$h$的各个分量，也就是编码器第$j$个神经元的输出。
$$\begin{array}{rl}\log {\mathcal{P}}_{model}(h)& =\log \prod _{j=1}^{\mathcal{K}}{\mathcal{P}}_{model}(h_j)\\ & =\sum _{j=1}^{\mathcal{K}}\log {\mathcal{P}}_{model}(h_j)\\ & =\sum _{j=1}^{\mathcal{K}}\log \left[\frac{\lambda }{2}\exp \{-\lambda |h_j|\}\right]\\ & =\underset{\mathcal{C}}{\sum _{j=1}^{\mathcal{K}}\log \frac{\lambda }{2}}-\underset{\Omega (h)}{\lambda \cdot \sum _{j=1}^{\mathcal{K}}|h_j|}\end{array}$$

个人理解：从先验的角度解释了稀疏惩罚$\Omega (h)$的作用。重点在于如何构建稀疏惩罚，也就是说，如何约束编码器神经元的输出$h$。

花书中的介绍，个人没有理解它的精髓。在不是真正意义上的先验的基础上，用先验去解释它。这里欢迎小伙伴们批评指正。

稀疏自编码器的构建

上面的$\text{Laplace}$分布是一种方式，也可以尝试其他的方式去约束编码器的输出$h$：

• 通过前馈神经网络的描述，可以将$h$的第$j$个神经元$h_j$表示为如下形式：
  其中$\sigma$表示激活函数。
  $$\begin{array}{rl}{h}_j& =\sigma \left({\mathcal{W}}_{x_1\iff j}\cdot x_1+{\mathcal{W}}_{x_2\iff j}\cdot x_2+\cdots +{\mathcal{W}}_{x_p\iff j}\cdot x_p+b_j\right)\\ & =\sigma ({\mathcal{W}}_{x\iff j}\cdot x+b_j)\end{array}$$

• 很明显，$h_j$可看作是一个关于样本特征$x_1,x_2,\cdots ,x_p$的函数$h_j(x)$。将样本集合$\mathcal{D}$内的所有样本$x^{(i)}(i=1,2,\cdots ,N)$带入到上式中，并取该结果的均值，结果记作$\widehat{{\rho }_j}$：
  也称$\widehat{{\rho }_j}$为‘平均激活度’$(\text{Average Activation})$
  $$\widehat{{\rho }_j}=\frac{1}{N}\sum _{i=1}^N\left[h_j(x^{(i)})\right]$$

• 在向下执行之前，我们有必要了解一下$\widehat{{\rho }_j}$，它的物理意义。为什么要这么设计它$?$如果从蒙特卡洛方法的反方向去考虑该式子，那么他可以被看作是：真实分布${\mathcal{P}}_{data}(x)$下，$h_j(x)$的期望结果：
  $$\widehat{{\rho }_j}\approx {\mathbb{E}}_{x^{(i)}\sim {\mathcal{P}}_{data}(x)}[h_j(x^{(i)})]$$
  这个期望的大小意味着什么：

  • 如果这个期望值大，意味着第$j$个神经元$h_j$对于样本$x^{(i)}(i=1,2,\cdots ,N)$ 的综合映射结果是不低的。 也就是说，$h_j$对于样本特征的描述更加完整，更加丰富；
    但这种特征描述方式违背了‘对其稀疏表示’的初衷，从而变成了单纯的复制。
  • 相反，如果这个期望值小，这意味着可能存在部分神经元活性较低/失活了，导致一部分神经元的输出接近于$0/$就是$0$。从而只能利用少数神经元完成编码器对特征的压缩。而这些抗打的(未失活的)神经元对应的特征就是$x$中最显著的信息。
  • 但我们也不能让其无限的小，甚至为$0$。如果是极限情况下让$\widehat{{\rho }_j}=0$，这些最显著信息对应的神经元也失活了，这个模型就没有意义了。

• 基于上述描述，我们可以设置一个目标值$\rho$，也称作稀疏性常数。这个值很小，例如$0.05$(讲义中的例子)，我们希望$\widehat{{\rho }_j}$向目标值$\rho$靠近，直至相等：
  $$\widehat{{\rho }_j}=\rho$$
  如何对这个靠近进行描述$?$我们将$\widehat{{\rho }_j}$和$\rho$看做是两个概率分布，使用$\mathcal{K}\mathcal{L}$散度对其进行描述：
  $\mathcal{K}\mathcal{L}$散度可理解为两概率分布$\rho ,\widehat{{\rho }_j}$之间的相似程度。有下界$0$,意味着$\rho =\widehat{{\rho }_j}$
  $$\mathcal{K}\mathcal{L}(\rho ||\widehat{{\rho }_j})=\rho \log \frac{\rho }{\widehat{{\rho }_j}}+(1-\rho )\log \frac{1-\rho }{1-\widehat{{\rho }_j}}$$
  当然，这里仅描述了第$j$个神经元$h_j$的情况。对于完整稀疏惩罚$\Omega (h)$可表示为：
  因为$\widehat{{\rho }_j}$是$h_j$的均值/期望，因此整个式子中只有$h_j(j=1,2,\cdots ,\mathcal{K})$是变量，满足‘稀疏惩罚项’的要求。
  $$\Omega (h)=\sum _{j=1}^{\mathcal{K}}\mathcal{K}\mathcal{L}(\rho ||\widehat{{\rho }_j})$$

最终，基于该方式的稀疏自编码器的策略可表示为：
$$\begin{array}{rl}{\mathcal{J}}_{sparse}(\mathcal{W},b)& =\mathcal{L}[x,g(f(x))]+\Omega (h)\\ & =\mathcal{J}(\mathcal{W},b)+\beta \cdot \sum _{j=1}^{\mathcal{K}}\mathcal{K}\mathcal{L}(\rho ||\widehat{{\rho }_j})\end{array}$$
回到题目，$\mathcal{C}$ 选项稀疏自编码器主要是针对编码器容量过完备情况下，对编码器神经元输出的稀疏惩罚。还是要和欠完备自编码器区分一下，正确。

相关参考：
《深度学习》(花书) P306 第14章 自编码器
深度学习 - 深度生成网络