KMP算法

KMP

KMP 算法是一个快速查找匹配串的算法，它的作用其实就是本题问题：如何快速在「原字符串」中找到「匹配字符串」。

而 KMP 算法的复杂度为 O(m+n)实际上是O(N),因为O(M)不可能大于O(N)

KMP 之所以能够在 O(m+n)复杂度内完成查找，是因为其能在「非完全匹配」的过程中提取到有效信息进行复用，以减少「重复匹配」的消耗。

KMP解决的问题

KMP解决,如何查 m 是否是 字符串 s 的字串
暴力解法 : 尝试每一个字符串的开头,来模拟是否匹配 , 时间复杂度(M*N)

 public int strStr(String ss, String pp) {
        int n = ss.length(), m = pp.length();
        char[] s = ss.toCharArray(), p = pp.toCharArray();
        // 枚举原串的「发起点」
        for (int i = 0; i <= n - m; i++) {
            // 从原串的「发起点」和匹配串的「首位」开始，尝试匹配
            int a = i, b = 0;
            while (b < m && s[a] == p[b]) {
                a++;
                b++;
            }
            // 如果能够完全匹配，返回原串的「发起点」下标
            if (b == m) return i;
        }
        return -1;
    }

KMP利用了字符串 M 的 每个字符,的最长前缀与后缀匹配的长度信息来加速移动

举例 :

next数组: 将 i 位置的字符的最长前缀信息存到一个数组 , 这个数组就是next 数组
第一个字符因为:没有字符 所以规定为 -1
第二个字符因为:只有一个字符 所以规定为 0

先不说加速next的过程 ,我们能办到 将所有字符的信息都求出来

然后现在来讲解,如何根据 next数组来加速 字符串 s 与字符串 m 的匹配过程

如果从第一个字符开始 , 经典过程是, 如果我发现第 i 个字符不相等的时候 ,我 s 字符串 的下标 要跳到第 2 个字符(从第二个字符开始 ) , m 字符串的下标要跳回到 第一个字符重新匹配 ,这就是经典过程
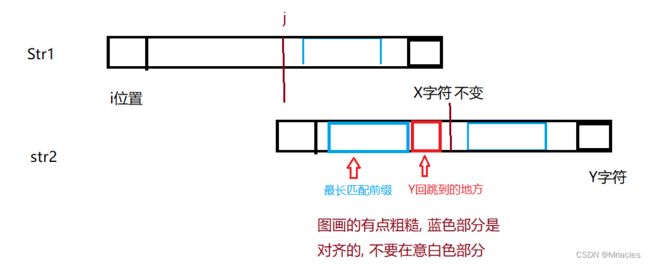
而 KMP 是, 当发现 i 位置开头 ,一路往下比, 直到比到 S字符不与 Y 字符不一致的时候 , 我能根据 next 数组, 的最大长度, Y位置最长前缀的后面 ,而 S 字符位置不变

举例 :

为什么 Y能回跳? 而X字符不变?

好得,接下来我们讲解如何加速 next数组信息的过程
我们知晓: next数组存放的都是最长的前缀匹配长度, 所以当下一个字符想要求 最长前缀长度的时候,我们可以利用next数组的信息, 我们直接跳到,之前的最长前缀长度的下一位来与当前字符进行匹配, 如果匹配成功,我们当前字符的最长前缀长度就是匹配到的前一个的前缀长度加1 , 如果匹配失败, 那我们就继续先前跳,知道跳到不能跳了,写成0

package Str;

public class KMP {
    //求一个字符串是不是另一个字符串的字串
//    整体复杂度O(N) 因为O(M)是不可能超过O(N)的
    public static int getIndexOf(String s,String m){
        if (s == null || m == null || m.length() >s.length() || m.length() < 1){
            return -1;
        }
        char[] str1 = s.toCharArray();
        char[] str2 = m.toCharArray();
        int i1= 0;
        int i2 = 0;
        int[] next = getNextArray(str2);//O(M)
        while (i1 < str1.length && i2 < str2.length){
            //i2 == str2.length的时候代表着,肯定匹配到了
            //O(N)
            if (str1[i1] == str2[i2]){
                //当前字符相等, 共同加加
                i1++;
                i2++;
            }else if (next[i2] == -1){
                //如果没有前缀和后缀匹配的,那没办法,只能往后走了
                i1++;
            }else {
                //如果不等,则找前缀和后缀最大的那个
                //要验证之前走过的是否有与str2匹配的情况
                i2 = next[i2];
            }
        }
        return i2 == str2.length ? i1-i2:-1;
    }
    public static int[] getNextArray(char[] ms){
        if (ms.length == 1){
            return new int[]{-1};
        }
        int[] next = new int[ms.length];
        next[0] = -1;
        next[1] = 0;
        int i = 2;
        int cn = 0;//即代表那个位置的值与i-1的值比
        while (i < next.length){
            if (ms[i-1] == ms[cn]){
                next[i++] = ++cn;
            }else if (cn > 0){
                //当前跳到cn位置的字符,和i-1位置的对应不上
                cn = next[cn];
            }else {
                //当cn为-1的时候,代表跳到了0下标的位置了
                next[i++] = 0;
            }
        }
        return next;
    }

    public static void main(String[] args) {
        String  s = "leetcode";
        String  m = "leeto";
        getIndexOf(s,m);
    }
}