循环神经网络和自然语言处理介绍||文本情感分类|| 循环神经网络||循环神经网络实现文本情感分类||Pytorch中的序列化容器
循环神经网络和自然语言处理介绍
目标
- 知道
token和tokenization - 知道
N-gram的概念和作用 - 知道文本向量化表示的方法
1. 文本的tokenization
1.1 概念和工具的介绍
tokenization就是通常所说的分词,分出的每一个词语我们把它称为token。
常见的分词工具很多,比如:
jieba分词:https://github.com/fxsjy/jieba- 清华大学的分词工具THULAC:
https://github.com/thunlp/THULAC-Python
1.2 中英文分词的方法
- 把句子转化为词语
- 比如:
我爱深度学习可以分为[我,爱, 深度学习]
- 比如:
- 把句子转化为单个字
- 比如:
我爱深度学习的token是[我,爱,深,度,学,习]
- 比如:
2. N-garm表示方法
前面我们说,句子可以用但个字,词来表示,但是有的时候,我们可以用2个、3个或者多个词来表示。
N-gram一组一组的词语,其中的N表示能够被一起使用的词的数量
例如:
In [59]: text = "深度学习(英语:deep learning)是机器学习的分支,是一种以人工神经网络为架构,对数据进行表征学习的算法。"
In [60]: cuted = jieba.lcut(text)
In [61]: [cuted[i:i+2] for i in range(len(cuted)-1)] #N-gram 中n=2时
Out[61]:[['深度', '学习'],
['学习', '('],
['(', '英语'],
['英语', ':'],
[':', 'deep'],
['deep', ' '],
[' ', 'learning'],
['learning', ')'],
[')', '是'],
['是', '机器'],
['机器', '学习'],
['学习', '的'],
['的', '分支'],
['分支', ','],
[',', '是'],
['是', '一种'],
['一种', '以'],
['以', '人工神经网络'],
['人工神经网络', '为'],
['为', '架构'],
['架构', ','],
[',', '对'],
['对', '数据'],
['数据', '进行'],
['进行', '表征'],
['表征', '学习'],
['学习', '的'],
['的', '算法'],
['算法', '。']]
在传统的机器学习中,使用N-gram方法往往能够取得非常好的效果,但是在深度学习比如RNN中会自带N-gram的效果。
3. 向量化
因为文本不能够直接被模型计算,所以需要将其转化为向量
把文本转化为向量有两种方法:
- 转化为one-hot编码
- 转化为word embedding
3.1 one-hot 编码
在one-hot编码中,每一个token使用一个长度为N的向量表示,N表示词典的数量
即:把待处理的文档进行分词或者是N-gram处理,然后进行去重得到词典,假设我们有一个文档:深度学习,那么进行one-hot处理后的结果如下:
| token | one-hot encoding |
|---|---|
| 深 | 1000 |
| 度 | 0100 |
| 学 | 0010 |
| 习 | 0001 |
3.2 word embedding
word embedding是深度学习中表示文本常用的一种方法。和one-hot编码不同,word embedding使用了浮点型的稠密矩阵来表示token。根据词典的大小,我们的向量通常使用不同的维度,例如100,256,300等。其中向量中的每一个值是一个参数,其初始值是随机生成的,之后会在训练的过程中进行学习而获得。
如果我们文本中有20000个词语,如果使用one-hot编码,那么我们会有20000*20000的矩阵,其中大多数的位置都为0,但是如果我们使用word embedding来表示的话,只需要20000* 维度,比如20000*300
形象的表示就是:
| token | num | vector |
|---|---|---|
| 词1 | 0 | [w11,w12,w13...w1N] ,其中N表示维度(dimension) |
| 词2 | 1 | [w21,w22,w23...w2N] |
| 词3 | 2 | [w31,w23,w33...w3N] |
| … | …. | … |
| 词m | m | [wm1,wm2,wm3...wmN],其中m表示词典的大小 |
我们会把所有的文本转化为向量,把句子用向量来表示
但是在这中间,我们会先把token使用数字来表示,再把数字使用向量来表示。
即:token---> num ---->vector
3.3 word embedding API
torch.nn.Embedding(num_embeddings,embedding_dim)
参数介绍:
num_embeddings:词典的大小embedding_dim:embedding的维度
使用方法:
embedding = nn.Embedding(vocab_size,300) #实例化
input_embeded = embedding(input) #进行embedding的操作
3.4 数据的形状变化
思考:每个batch中的每个句子有10个词语,经过形状为[20,4]的Word emebedding之后,原来的句子会变成什么形状?
每个词语用长度为4的向量表示,所以,最终句子会变为[batch_size,10,4]的形状。
增加了一个维度,这个维度是embedding的dim
文本情感分类
目标
- 知道文本处理的基本方法
- 能够使用数据实现情感分类的
1. 案例介绍
为了对前面的word embedding这种常用的文本向量化的方法进行巩固,这里我们会完成一个文本情感分类的案例
现在我们有一个经典的数据集IMDB数据集,地址:http://ai.stanford.edu/~amaas/data/sentiment/,这是一份包含了5万条流行电影的评论数据,其中训练集25000条,测试集25000条。数据格式如下:
下图左边为名称,其中名称包含两部分,分别是序号和情感评分,(1-4为neg,5-10为pos),右边为评论内容
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-y8HCv1zP-1630156172569)(…/images/1.3/样本名称.png)]
根据上述的样本,需要使用pytorch完成模型,实现对评论情感进行预测
2. 思路分析
首先可以把上述问题定义为分类问题,情感评分分为1-10,10个类别(也可以理解为回归问题,这里当做分类问题考虑)。那么根据之前的经验,我们的大致流程如下:
- 准备数据集
- 构建模型
- 模型训练
- 模型评估
知道思路之后,那么我们一步步来完成上述步骤
3. 准备数据集
准备数据集和之前的方法一样,实例化dataset,准备dataloader,最终我们的数据可以处理成如下格式:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-iZnxYhOX-1630156172570)(…/images/1.3/情感分类-data加载1.png)]
其中有两点需要注意:
- 如何完成基础打Dataset的构建和Dataloader的准备
- 每个batch中文本的长度不一致的问题如何解决
- 每个batch中的文本如何转化为数字序列
3.1 基础Dataset的准备
import torch
from torch.utils.data import DataLoader,Dataset
import os
import re
data_base_path = r"data\aclImdb"
#1. 定义tokenize的方法
def tokenize(text):
# fileters = '!"#$%&()*+,-./:;<=>?@[\\]^_`{|}~\t\n'
fileters = ['!','"','#','$','%','&','\(','\)','\*','\+',',','-','\.','/',':',';','<','=','>','\?','@'
,'\[','\\','\]','^','_','`','\{','\|','\}','~','\t','\n','\x97','\x96','”','“',]
text = re.sub("<.*?>"," ",text,flags=re.S)
text = re.sub("|".join(fileters)," ",text,flags=re.S)
return [i.strip() for i in text.split()]
#2. 准备dataset
class ImdbDataset(Dataset):
def __init__(self,mode):
super(ImdbDataset,self).__init__()
if mode=="train":
text_path = [os.path.join(data_base_path,i) for i in ["train/neg","train/pos"]]
else:
text_path = [os.path.join(data_base_path,i) for i in ["test/neg","test/pos"]]
self.total_file_path_list = []
for i in text_path:
self.total_file_path_list.extend([os.path.join(i,j) for j in os.listdir(i)])
def __getitem__(self, idx):
cur_path = self.total_file_path_list[idx]
cur_filename = os.path.basename(cur_path)
label = int(cur_filename.split("_")[-1].split(".")[0]) -1 #处理标题,获取label,转化为从[0-9]
text = tokenize(open(cur_path).read().strip()) #直接按照空格进行分词
return label,text
def __len__(self):
return len(self.total_file_path_list)
# 2. 实例化,准备dataloader
dataset = ImdbDataset(mode="train")
dataloader = DataLoader(dataset=dataset,batch_size=2,shuffle=True)
#3. 观察数据输出结果
for idx,(label,text) in enumerate(dataloader):
print("idx:",idx)
print("table:",label)
print("text:",text)
break
输出如下:
idx: 0
table: tensor([3, 1])
text: [('I', 'Want'), ('thought', 'a'), ('this', 'great'), ('was', 'recipe'), ('a', 'for'), ('great', 'failure'), ('idea', 'Take'), ('but', 'a'), ('boy', 's'), ('was', 'y'), ('it', 'plot'), ('poorly', 'add'), ('executed', 'in'), ('We', 'some'), ('do', 'weak'), ('get', 'completely'), ('a', 'undeveloped'), ('broad', 'characters'), ('sense', 'and'), ('of', 'than'), ('how', 'throw'), ('complex', 'in'), ('and', 'the'), ('challenging', 'worst'), ('the', 'special'), ('backstage', 'effects'), ('operations', 'a'), ('of', 'horror'), ('a', 'movie'), ('show', 'has'), ('are', 'known'), ('but', 'Let'), ('virtually', 'stew'), ('no', 'for'), ...('show', 'somehow'), ('rather', 'destroy'), ('than', 'every'), ('anything', 'copy'), ('worth', 'of'), ('watching', 'this'), ('for', 'film'), ('its', 'so'), ('own', 'it'), ('merit', 'will')]
明显,其中的text内容出现对应,和想象的不太相似,出现问题的原因在于Dataloader中的参数collate_fn
collate_fn的默认值为torch自定义的default_collate,collate_fn的作用就是对每个batch进行处理,而默认的default_collate处理出错。
解决问题的思路:
手段1:考虑先把数据转化为数字序列,观察其结果是否符合要求,之前使用DataLoader并未出现类似错误
手段2:考虑自定义一个collate_fn,观察结果
这里使用方式2,自定义一个collate_fn,然后观察结果:
def collate_fn(batch):
#batch是list,其中是一个一个元组,每个元组是dataset中__getitem__的结果
batch = list(zip(*batch))
labes = torch.tensor(batch[0],dtype=torch.int32)
texts = batch[1]
del batch
return labes,texts
dataloader = DataLoader(dataset=dataset,batch_size=2,shuffle=True,collate_fn=collate_fn)
#此时输出正常
for idx,(label,text) in enumerate(dataloader):
print("idx:",idx)
print("table:",label)
print("text:",text)
break
3.2 文本序列化
再介绍word embedding的时候,我们说过,不会直接把文本转化为向量,而是先转化为数字,再把数字转化为向量,那么这个过程该如何实现呢?
这里我们可以考虑把文本中的每个词语和其对应的数字,使用字典保存,同时实现方法把句子通过字典映射为包含数字的列表。
实现文本序列化之前,考虑以下几点:
- 如何使用字典把词语和数字进行对应
- 不同的词语出现的次数不尽相同,是否需要对高频或者低频词语进行过滤,以及总的词语数量是否需要进行限制
- 得到词典之后,如何把句子转化为数字序列,如何把数字序列转化为句子
- 不同句子长度不相同,每个batch的句子如何构造成相同的长度(可以对短句子进行填充,填充特殊字符)
- 对于新出现的词语在词典中没有出现怎么办(可以使用特殊字符代理)
思路分析:
- 对所有句子进行分词
- 词语存入字典,根据次数对词语进行过滤,并统计次数
- 实现文本转数字序列的方法
- 实现数字序列转文本方法
import numpy as np
class Word2Sequence():
UNK_TAG = "UNK"
PAD_TAG = "PAD"
UNK = 0
PAD = 1
def __init__(self):
self.dict = {
self.UNK_TAG :self.UNK,
self.PAD_TAG :self.PAD
}
self.fited = False
def to_index(self,word):
"""word -> index"""
assert self.fited == True,"必须先进行fit操作"
return self.dict.get(word,self.UNK)
def to_word(self,index):
"""index -> word"""
assert self.fited , "必须先进行fit操作"
if index in self.inversed_dict:
return self.inversed_dict[index]
return self.UNK_TAG
def __len__(self):
return self(self.dict)
def fit(self, sentences, min_count=1, max_count=None, max_feature=None):
"""
:param sentences:[[word1,word2,word3],[word1,word3,wordn..],...]
:param min_count: 最小出现的次数
:param max_count: 最大出现的次数
:param max_feature: 总词语的最大数量
:return:
"""
count = {}
for sentence in sentences:
for a in sentence:
if a not in count:
count[a] = 0
count[a] += 1
# 比最小的数量大和比最大的数量小的需要
if min_count is not None:
count = {k: v for k, v in count.items() if v >= min_count}
if max_count is not None:
count = {k: v for k, v in count.items() if v <= max_count}
# 限制最大的数量
if isinstance(max_feature, int):
count = sorted(list(count.items()), key=lambda x: x[1])
if max_feature is not None and len(count) > max_feature:
count = count[-int(max_feature):]
for w, _ in count:
self.dict[w] = len(self.dict)
else:
for w in sorted(count.keys()):
self.dict[w] = len(self.dict)
self.fited = True
# 准备一个index->word的字典
self.inversed_dict = dict(zip(self.dict.values(), self.dict.keys()))
def transform(self, sentence,max_len=None):
"""
实现吧句子转化为数组(向量)
:param sentence:
:param max_len:
:return:
"""
assert self.fited, "必须先进行fit操作"
if max_len is not None:
r = [self.PAD]*max_len
else:
r = [self.PAD]*len(sentence)
if max_len is not None and len(sentence)>max_len:
sentence=sentence[:max_len]
for index,word in enumerate(sentence):
r[index] = self.to_index(word)
return np.array(r,dtype=np.int64)
def inverse_transform(self,indices):
"""
实现从数组 转化为文字
:param indices: [1,2,3....]
:return:[word1,word2.....]
"""
sentence = []
for i in indices:
word = self.to_word(i)
sentence.append(word)
return sentence
if __name__ == '__main__':
w2s = Word2Sequence()
w2s.fit([
["你", "好", "么"],
["你", "好", "哦"]])
print(w2s.dict)
print(w2s.fited)
print(w2s.transform(["你","好","嘛"]))
print(w2s.transform(["你好嘛"],max_len=10))
完成了wordsequence之后,接下来就是保存现有样本中的数据字典,方便后续的使用。
实现对IMDB数据的处理和保存
#1. 对IMDB的数据记性fit操作
def fit_save_word_sequence():
from wordSequence import Word2Sequence
ws = Word2Sequence()
train_path = [os.path.join(data_base_path,i) for i in ["train/neg","train/pos"]]
total_file_path_list = []
for i in train_path:
total_file_path_list.extend([os.path.join(i, j) for j in os.listdir(i)])
for cur_path in tqdm(total_file_path_list,ascii=True,desc="fitting"):
ws.fit(tokenize(open(cur_path).read().strip()))
ws.build_vocab()
# 对wordSequesnce进行保存
pickle.dump(ws,open("./model/ws.pkl","wb"))
#2. 在dataset中使用wordsequence
ws = pickle.load(open("./model/ws.pkl","rb"))
def collate_fn(batch):
MAX_LEN = 500
#MAX_LEN = max([len(i) for i in texts]) #取当前batch的最大值作为batch的最大长度
batch = list(zip(*batch))
labes = torch.tensor(batch[0],dtype=torch.int)
texts = batch[1]
#获取每个文本的长度
lengths = [len(i) if len(i)<MAX_LEN else MAX_LEN for i in texts]
texts = torch.tensor([ws.transform(i, MAX_LEN) for i in texts])
del batch
return labes,texts,lengths
#3. 获取输出
dataset = ImdbDataset(ws,mode="train")
dataloader = DataLoader(dataset=dataset,batch_size=20,shuffle=True,collate_fn=collate_fn)
for idx,(label,text,length) in enumerate(dataloader):
print("idx:",idx)
print("table:",label)
print("text:",text)
print("length:",length)
break
输出如下
idx: 0
table: tensor([ 7, 4, 3, 8, 1, 10, 7, 10, 7, 2, 1, 8, 1, 2, 2, 4, 7, 10,
1, 4], dtype=torch.int32)
text: tensor([[ 50983, 77480, 82366, ..., 1, 1, 1],
[ 54702, 57262, 102035, ..., 80474, 56457, 63180],
[ 26991, 57693, 88450, ..., 1, 1, 1],
...,
[ 51138, 73263, 80428, ..., 1, 1, 1],
[ 7022, 78114, 83498, ..., 1, 1, 1],
[ 5353, 101803, 99148, ..., 1, 1, 1]])
length: [296, 500, 221, 132, 74, 407, 500, 130, 54, 217, 80, 322, 72, 156, 94, 270, 317, 117, 200, 379]
思考:前面我们自定义了MAX_LEN作为句子的最大长度,如果我们需要把每个batch中的最长的句子长度作为当前batch的最大长度,该如何实现?
4. 构建模型
这里我们只练习使用word embedding,所以模型只有一层,即:
- 数据经过word embedding
- 数据通过全连接层返回结果,计算
log_softmax
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch import optim
from build_dataset import get_dataloader,ws,MAX_LEN
class IMDBModel(nn.Module):
def __init__(self,max_len):
super(IMDBModel,self).__init__()
self.embedding = nn.Embedding(len(ws),300,padding_idx=ws.PAD) #[N,300]
self.fc = nn.Linear(max_len*300,10) #[max_len*300,10]
def forward(self, x):
embed = self.embedding(x) #[batch_size,max_len,300]
embed = embed.view(x.size(0),-1)
out = self.fc(embed)
return F.log_softmax(out,dim=-1)
5. 模型的训练和评估
训练流程和之前相同
- 实例化模型,损失函数,优化器
- 遍历dataset_loader,梯度置为0,进行向前计算
- 计算损失,反向传播优化损失,更新参数
train_batch_size = 128
test_batch_size = 1000
imdb_model = IMDBModel(MAX_LEN)
optimizer = optim.Adam(imdb_model.parameters())
criterion = nn.CrossEntropyLoss()
def train(epoch):
mode = True
imdb_model.train(mode)
train_dataloader =get_dataloader(mode,train_batch_size)
for idx,(target,input,input_lenght) in enumerate(train_dataloader):
optimizer.zero_grad()
output = imdb_model(input)
loss = F.nll_loss(output,target) #traget需要是[0,9],不能是[1-10]
loss.backward()
optimizer.step()
if idx %10 == 0:
print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
epoch, idx * len(input), len(train_dataloader.dataset),
100. * idx / len(train_dataloader), loss.item()))
torch.save(imdb_model.state_dict(), "model/mnist_net.pkl")
torch.save(optimizer.state_dict(), 'model/mnist_optimizer.pkl')
def test():
test_loss = 0
correct = 0
mode = False
imdb_model.eval()
test_dataloader = get_dataloader(mode, test_batch_size)
with torch.no_grad():
for target, input, input_lenght in test_dataloader:
output = imdb_model(input)
test_loss += F.nll_loss(output, target,reduction="sum")
pred = torch.max(output,dim=-1,keepdim=False)[-1]
correct = pred.eq(target.data).sum()
test_loss = test_loss/len(test_dataloader.dataset)
print('\nTest set: Avg. loss: {:.4f}, Accuracy: {}/{} ({:.2f}%)\n'.format(
test_loss, correct, len(test_dataloader.dataset),
100. * correct / len(test_dataloader.dataset)))
if __name__ == '__main__':
test()
for i in range(3):
train(i)
test()
这里我们仅仅使用了一层全连接层,其分类效果不会很好,这里重点是理解常见的模型流程和word embedding的使用方法
循环神经网络
目标
- 能够说出循环神经网络的概念和作用
- 能够说出循环神经网络的类型和应用场景
- 能够说出LSTM的作用和原理
- 能够说出GRU的作用和原理
1. 循环神经网络的介绍
为什么有了神经网络还需要有循环神经网络?
在普通的神经网络中,信息的传递是单向的,这种限制虽然使得网络变得更容易学习,但在一定程度上也减弱了神经网络模型的能力。特别是在很多现实任务中,网络的输出不仅和当前时刻的输入相关,也和其过去一段时间的输出相关。此外,普通网络难以处理时序数据,比如视频、语音、文本等,时序数据的长度一般是不固定的,而前馈神经网络要求输入和输出的维数都是固定的,不能任意改变。因此,当处理这一类和时序相关的问题时,就需要一种能力更强的模型。
循环神经网络(Recurrent Neural Network,RNN)是一类具有短期记忆能力的神经网络。在循环神经网络中,神经元不但可以接受其它神经元的信息,也可以接受自身的信息,形成具有环路的网络结构。换句话说:神经元的输出可以在下一个时间步直接作用到自身(
入)
通过简化图,我们看到RNN比传统的神经网络多了一个循环圈,这个循环表示的就是在下一个时间步(Time Step)上会返回作为输入的一部分,我们把RNN在时间点上展开,得到的图形如下:
或者是:
在不同的时间步,RNN的输入都将与之前的时间状态有关, t n t_n tn时刻网络的输出结果是该时刻的输入和所有历史共同作用的结果,这就达到了对时间序列建模的目的。
RNN的不同表示和功能可以通过下图看出:
- 图1:固定长度的输入和输出 (e.g. 图像分类)
- 图2:序列输出 (e.g.图像转文字)
- 图3:数列输入 (e.g. 文本分类)
- 图4:异步的序列输入和输出(e.g.文本翻译).
- 图5:同步的序列输入和输出 (e.g. 根据视频的每一帧来对视频进行分类)
2. LSTM和GRU
2.1 LSTM的基础介绍
假如现在有这样一个需求,根据现有文本预测下一个词语,比如天上的云朵漂浮在__,通过间隔不远的位置就可以预测出来词语是天上,但是对于其他一些句子,可能需要被预测的词语在前100个词语之前,那么此时由于间隔非常大,随着间隔的增加可能会导致真实的预测值对结果的影响变的非常小,而无法非常好的进行预测(RNN中的长期依赖问题(long-Term Dependencies))
那么为了解决这个问题需要LSTM(Long Short-Term Memory网络)
LSTM是一种RNN特殊的类型,可以学习长期依赖信息。在很多问题上,LSTM都取得相当巨大的成功,并得到了广泛的应用。
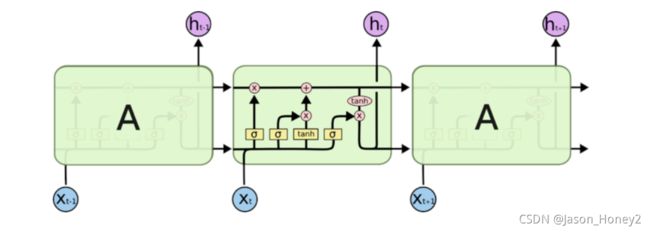
一个LSMT的单元就是下图中的一个绿色方框中的内容:
其中 σ \sigma σ表示sigmod函数,其他符号的含义:
2.2 LSTM的核心
LSTM的核心在于单元(细胞)中的状态,也就是上图中最上面的那根线。
但是如果只有上面那一条线,那么没有办法实现信息的增加或者删除,所以在LSTM是通过一个叫做门的结构实现,门可以选择让信息通过或者不通过。
这个门主要是通过sigmoid和点乘(pointwise multiplication)实现的
我们都知道, s i g m o i d sigmoid sigmoid的取值范围是在(0,1)之间,如果接近0表示不让任何信息通过,如果接近1表示所有的信息都会通过
2.3 逐步理解LSTM
2.3.1 遗忘门
遗忘门通过sigmoid函数来决定哪些信息会被遗忘
在下图就是 h t − 1 和 x t h_{t-1}和x_t ht−1和xt进行合并(concat)之后乘上权重和偏置,通过sigmoid函数,输出0-1之间的一个值,这个值会和前一次的细胞状态( C t − 1 C_{t-1} Ct−1)进行点乘,从而决定遗忘或者保留
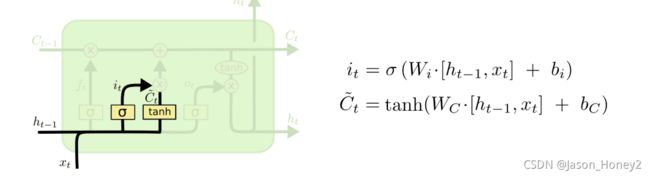
2.3.2 输入门
下一步就是决定哪些新的信息会被保留,这个过程有两步:
- 一个被称为
输入门的sigmoid 层决定哪些信息会被更新 tanh会创造一个新的候选向量 C ~ t \widetilde{C}_{t} C t,后续可能会被添加到细胞状态中
例如:
我昨天吃了苹果,今天我想吃菠萝,在这个句子中,通过遗忘门可以遗忘苹果,同时更新新的主语为菠萝
现在就可以更新旧的细胞状态 C t − 1 C_{t-1} Ct−1为新的 C t C_{ t } Ct 了。
更新的构成很简单就是:
- 旧的细胞状态和遗忘门的结果相乘
- 然后加上 输入门和tanh相乘的结果
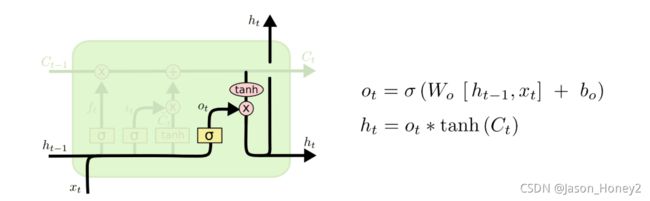
2.3.3 输出门
最后,我们需要决定什么信息会被输出,也是一样这个输出经过变换之后会通过sigmoid函数的结果来决定那些细胞状态会被输出。
步骤如下:
- 前一次的输出和当前时间步的输入的组合结果通过sigmoid函数进行处理得到 O t O_t Ot
- 更新后的细胞状态 C t C_t Ct会经过tanh层的处理,把数据转化到(-1,1)的区间
- tanh处理后的结果和 O t O_t Ot进行相乘,把结果输出同时传到下一个LSTM的单元
2.4 GRU,LSTM的变形
GRU(Gated Recurrent Unit),是一种LSTM的变形版本, 它将遗忘和输入门组合成一个“更新门”。它还合并了单元状态和隐藏状态,并进行了一些其他更改,由于他的模型比标准LSTM模型简单,所以越来越受欢迎。
LSTM内容参考地址:https://colah.github.io/posts/2015-08-Understanding-LSTMs/
3. 双向LSTM
单向的 RNN,是根据前面的信息推出后面的,但有时候只看前面的词是不够的, 可能需要预测的词语和后面的内容也相关,那么此时需要一种机制,能够让模型不仅能够从前往后的具有记忆,还需要从后往前需要记忆。此时双向LSTM就可以帮助我们解决这个问题
由于是双向LSTM,所以每个方向的LSTM都会有一个输出,最终的输出会有2部分,所以往往需要concat的操作
循环神经网络实现文本情感分类
目标
- 知道LSTM和GRU的使用方法及输入输出的格式
- 能够应用LSTM和GRU实现文本情感分类
1. Pytorch中LSTM和GRU模块使用
1.1 LSTM介绍
LSTM和GRU都是由torch.nn提供
通过观察文档,可知LSMT的参数,
torch.nn.LSTM(input_size,hidden_size,num_layers,batch_first,dropout,bidirectional)
input_size:输入数据的形状,即embedding_dimhidden_size:隐藏层神经元的数量,即每一层有多少个LSTM单元num_layer:即RNN的中LSTM单元的层数batch_first:默认值为False,输入的数据需要[seq_len,batch,feature],如果为True,则为[batch,seq_len,feature]dropout:dropout的比例,默认值为0。dropout是一种训练过程中让部分参数随机失活的一种方式,能够提高训练速度,同时能够解决过拟合的问题。这里是在LSTM的最后一层,对每个输出进行dropoutbidirectional:是否使用双向LSTM,默认是False
实例化LSTM对象之后,不仅需要传入数据,还需要前一次的h_0(前一次的隐藏状态)和c_0(前一次memory)
即:lstm(input,(h_0,c_0))
LSTM的默认输出为output, (h_n, c_n)
output:(seq_len, batch, num_directions * hidden_size)—>batch_first=Falseh_n:(num_layers * num_directions, batch, hidden_size)c_n:(num_layers * num_directions, batch, hidden_size)
1.2 LSTM使用示例
假设数据输入为 input ,形状是[10,20],假设embedding的形状是[100,30]
则LSTM使用示例如下:
batch_size =10
seq_len = 20
embedding_dim = 30
word_vocab = 100
hidden_size = 18
num_layer = 2
#准备输入数据
input = torch.randint(low=0,high=100,size=(batch_size,seq_len))
#准备embedding
embedding = torch.nn.Embedding(word_vocab,embedding_dim)
lstm = torch.nn.LSTM(embedding_dim,hidden_size,num_layer)
#进行mebed操作
embed = embedding(input) #[10,20,30]
#转化数据为batch_first=False
embed = embed.permute(1,0,2) #[20,10,30]
#初始化状态, 如果不初始化,torch默认初始值为全0
h_0 = torch.rand(num_layer,batch_size,hidden_size)
c_0 = torch.rand(num_layer,batch_size,hidden_size)
output,(h_1,c_1) = lstm(embed,(h_0,c_0))
#output [20,10,1*18]
#h_1 [2,10,18]
#c_1 [2,10,18]
输出如下
In [122]: output.size()
Out[122]: torch.Size([20, 10, 18])
In [123]: h_1.size()
Out[123]: torch.Size([2, 10, 18])
In [124]: c_1.size()
Out[124]: torch.Size([2, 10, 18])
通过前面的学习,我们知道,最后一次的h_1应该和output的最后一个time step的输出是一样的
通过下面的代码,我们来验证一下:
In [179]: a = output[-1,:,:]
In [180]: a.size()
Out[180]: torch.Size([10, 18])
In [183]: b.size()
Out[183]: torch.Size([10, 18])
In [184]: a == b
Out[184]:
tensor([[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]],
dtype=torch.uint8)
1.3 GRU的使用示例
GRU模块torch.nn.GRU,和LSTM的参数相同,含义相同,具体可参考文档
但是输入只剩下gru(input,h_0),输出为output, h_n
其形状为:
output:(seq_len, batch, num_directions * hidden_size)h_n:(num_layers * num_directions, batch, hidden_size)
大家可以使用上述代码,观察GRU的输出形式
1.4 双向LSTM
如果需要使用双向LSTM,则在实例化LSTM的过程中,需要把LSTM中的bidriectional设置为True,同时h_0和c_0使用num_layer*2
观察效果,输出为
batch_size =10 #句子的数量
seq_len = 20 #每个句子的长度
embedding_dim = 30 #每个词语使用多长的向量表示
word_vocab = 100 #词典中词语的总数
hidden_size = 18 #隐层中lstm的个数
num_layer = 2 #多少个隐藏层
input = torch.randint(low=0,high=100,size=(batch_size,seq_len))
embedding = torch.nn.Embedding(word_vocab,embedding_dim)
lstm = torch.nn.LSTM(embedding_dim,hidden_size,num_layer,bidirectional=True)
embed = embedding(input) #[10,20,30]
#转化数据为batch_first=False
embed = embed.permute(1,0,2) #[20,10,30]
h_0 = torch.rand(num_layer*2,batch_size,hidden_size)
c_0 = torch.rand(num_layer*2,batch_size,hidden_size)
output,(h_1,c_1) = lstm(embed,(h_0,c_0))
In [135]: output.size()
Out[135]: torch.Size([20, 10, 36])
In [136]: h_1.size()
Out[136]: torch.Size([4, 10, 18])
In [137]: c_1.size()
Out[137]: torch.Size([4, 10, 18])
在单向LSTM中,最后一个time step的输出的前hidden_size个和最后一层隐藏状态h_1的输出相同,那么双向LSTM呢?
双向LSTM中:
output:按照正反计算的结果顺序在第2个维度进行拼接,正向第一个拼接反向的最后一个输出
hidden state:按照得到的结果在第0个维度进行拼接,正向第一个之后接着是反向第一个
-
前向的LSTM中,最后一个time step的输出的前hidden_size个和最后一层向前传播h_1的输出相同
-
示例:
-
#-1是前向LSTM的最后一个,前18是前hidden_size个 In [188]: a = output[-1,:,:18] #前项LSTM中最后一个time step的output In [189]: b = h_1[-2,:,:] #倒数第二个为前向 In [190]: a.size() Out[190]: torch.Size([10, 18]) In [191]: b.size() Out[191]: torch.Size([10, 18]) In [192]: a == b Out[192]: tensor([[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]], dtype=torch.uint8)
-
-
后向LSTM中,最后一个time step的输出的后hidden_size个和最后一层后向传播的h_1的输出相同
-
示例
-
#0 是反向LSTM的最后一个,后18是后hidden_size个 In [196]: c = output[0,:,18:] #后向LSTM中的最后一个输出 In [197]: d = h_1[-1,:,:] #后向LSTM中的最后一个隐藏层状态 In [198]: c == d Out[198]: tensor([[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1], [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]], dtype=torch.uint8)
-
1.4 LSTM和GRU的使用注意点
- 第一次调用之前,需要初始化隐藏状态,如果不初始化,默认创建全为0的隐藏状态
- 往往会使用LSTM or GRU 的输出的最后一维的结果,来代表LSTM、GRU对文本处理的结果,其形状为
[batch, num_directions*hidden_size]。- 并不是所有模型都会使用最后一维的结果
- 如果实例化LSTM的过程中,batch_first=False,则
output[-1] or output[-1,:,:]可以获取最后一维 - 如果实例化LSTM的过程中,batch_first=True,则
output[:,-1,:]可以获取最后一维
- 如果结果是
(seq_len, batch_size, num_directions * hidden_size),需要把它转化为(batch_size,seq_len, num_directions * hidden_size)的形状,不能够不是view等变形的方法,需要使用output.permute(1,0,2),即交换0和1轴,实现上述效果 - 使用双向LSTM的时候,往往会分别使用每个方向最后一次的output,作为当前数据经过双向LSTM的结果
- 即:
torch.cat([h_1[-2,:,:],h_1[-1,:,:]],dim=-1) - 最后的表示的size是
[batch_size,hidden_size*2]
- 即:
- 上述内容在GRU中同理
2. 使用LSTM完成文本情感分类
在前面,我们使用了word embedding去实现了toy级别的文本情感分类,那么现在我们在这个模型中添加上LSTM层,观察分类效果。
为了达到更好的效果,对之前的模型做如下修改
- MAX_LEN = 200
- 构建dataset的过程,把数据转化为2分类的问题,pos为1,neg为0,否则25000个样本完成10个类别的划分数据量是不够的
- 在实例化LSTM的时候,使用dropout=0.5,在model.eval()的过程中,dropout自动会为0
2.1 修改模型
class IMDBLstmmodel(nn.Module):
def __init__(self):
super(IMDBLstmmodel,self).__init__()
self.hidden_size = 64
self.embedding_dim = 200
self.num_layer = 2
self.bidriectional = True
self.bi_num = 2 if self.bidriectional else 1
self.dropout = 0.5
#以上部分为超参数,可以自行修改
self.embedding = nn.Embedding(len(ws),self.embedding_dim,padding_idx=ws.PAD) #[N,300]
self.lstm = nn.LSTM(self.embedding_dim,self.hidden_size,self.num_layer,bidirectional=True,dropout=self.dropout)
#使用两个全连接层,中间使用relu激活函数
self.fc = nn.Linear(self.hidden_size*self.bi_num,20)
self.fc2 = nn.Linear(20,2)
def forward(self, x):
x = self.embedding(x)
x = x.permute(1,0,2) #进行轴交换
h_0,c_0 = self.init_hidden_state(x.size(1))
_,(h_n,c_n) = self.lstm(x,(h_0,c_0))
#只要最后一个lstm单元处理的结果,这里多去的hidden state
out = torch.cat([h_n[-2, :, :], h_n[-1, :, :]], dim=-1)
out = self.fc(out)
out = F.relu(out)
out = self.fc2(out)
return F.log_softmax(out,dim=-1)
def init_hidden_state(self,batch_size):
h_0 = torch.rand(self.num_layer * self.bi_num, batch_size, self.hidden_size).to(device)
c_0 = torch.rand(self.num_layer * self.bi_num, batch_size, self.hidden_size).to(device)
return h_0,c_0
2.2 完成训练和测试代码
为了提高程序的运行速度,可以考虑把模型放在gup上运行,那么此时需要处理一下几点:
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")model.to(device)- 除了上述修改外,涉及计算的所有tensor都需要转化为CUDA的tensor
- 初始化的
h_0,c_0 - 训练集和测试集的
input,traget
- 初始化的
- 在最后可以通过
tensor.cpu()转化为torch的普通tensor
train_batch_size = 64
test_batch_size = 5000
# imdb_model = IMDBModel(MAX_LEN) #基础model
imdb_model = IMDBLstmmodel().to(device) #在gpu上运行,提高运行速度
# imdb_model.load_state_dict(torch.load("model/mnist_net.pkl"))
optimizer = optim.Adam(imdb_model.parameters())
criterion = nn.CrossEntropyLoss()
def train(epoch):
mode = True
imdb_model.train(mode)
train_dataloader =get_dataloader(mode,train_batch_size)
for idx,(target,input,input_lenght) in enumerate(train_dataloader):
target = target.to(device)
input = input.to(device)
optimizer.zero_grad()
output = imdb_model(input)
loss = F.nll_loss(output,target) #traget需要是[0,9],不能是[1-10]
loss.backward()
optimizer.step()
if idx %10 == 0:
pred = torch.max(output, dim=-1, keepdim=False)[-1]
acc = pred.eq(target.data).cpu().numpy().mean()*100.
print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}\t ACC: {:.6f}'.format(epoch, idx * len(input), len(train_dataloader.dataset),
100. * idx / len(train_dataloader), loss.item(),acc))
torch.save(imdb_model.state_dict(), "model/mnist_net.pkl")
torch.save(optimizer.state_dict(), 'model/mnist_optimizer.pkl')
def test():
mode = False
imdb_model.eval()
test_dataloader = get_dataloader(mode, test_batch_size)
with torch.no_grad():
for idx,(target, input, input_lenght) in enumerate(test_dataloader):
target = target.to(device)
input = input.to(device)
output = imdb_model(input)
test_loss = F.nll_loss(output, target,reduction="mean")
pred = torch.max(output,dim=-1,keepdim=False)[-1]
correct = pred.eq(target.data).sum()
acc = 100. * pred.eq(target.data).cpu().numpy().mean()
print('idx: {} Test set: Avg. loss: {:.4f}, Accuracy: {}/{} ({:.2f}%)\n'.format(idx,test_loss, correct, target.size(0),acc))
if __name__ == "__main__":
test()
for i in range(10):
train(i)
test()
2.3 模型训练的最终输出
...
Train Epoch: 9 [20480/25000 (82%)] Loss: 0.017165 ACC: 100.000000
Train Epoch: 9 [21120/25000 (84%)] Loss: 0.021572 ACC: 98.437500
Train Epoch: 9 [21760/25000 (87%)] Loss: 0.058546 ACC: 98.437500
Train Epoch: 9 [22400/25000 (90%)] Loss: 0.045248 ACC: 98.437500
Train Epoch: 9 [23040/25000 (92%)] Loss: 0.027622 ACC: 98.437500
Train Epoch: 9 [23680/25000 (95%)] Loss: 0.097722 ACC: 95.312500
Train Epoch: 9 [24320/25000 (97%)] Loss: 0.026713 ACC: 98.437500
Train Epoch: 9 [15600/25000 (100%)] Loss: 0.006082 ACC: 100.000000
idx: 0 Test set: Avg. loss: 0.8794, Accuracy: 4053/5000 (81.06%)
idx: 1 Test set: Avg. loss: 0.8791, Accuracy: 4018/5000 (80.36%)
idx: 2 Test set: Avg. loss: 0.8250, Accuracy: 4087/5000 (81.74%)
idx: 3 Test set: Avg. loss: 0.8380, Accuracy: 4074/5000 (81.48%)
idx: 4 Test set: Avg. loss: 0.8696, Accuracy: 4027/5000 (80.54%)
可以看到模型的测试准确率稳定在81%左右。
大家可以把上述代码改为GRU,或者多层LSTM继续尝试,观察效果
Pytorch中的序列化容器
目标
- 知道梯度消失和梯度爆炸的原理和解决方法
- 能够使用
nn.Sequential完成模型的搭建 - 知道
nn.BatchNorm1d的使用方法 - 知道
nn.Dropout的使用方法
1. 梯度消失和梯度爆炸
在使用pytorch中的序列化 容器之前,我们先来了解一下常见的梯度消失和梯度爆炸的问题
1.1 梯度消失
假设我们有四层极简神经网络:每层只有一个神经元
获 取 w 1 的 梯 度 有 : ▽ w 1 = x 1 ∗ f ( a 1 ) ’ ∗ w 2 ∗ f ( b 1 ) ’ ∗ w 3 ∗ ▽ o u t 获取w1的梯度有:▽w1 = x1*f(a1)’*w2*f(b1)’*w3*▽out 获取w1的梯度有:▽w1=x1∗f(a1)’∗w2∗f(b1)’∗w3∗▽out
假设我们使用sigmoid激活函数,即f为sigmoid函数,sigmoid的导数如下图
假设每层都取得sigmoid导函数的最大值1/4,那么在反向传播时, X 1 = 0.5 , w 1 = w 2 = w 3 = 0.5 X1=0.5,w1=w2=w3=0.5 X1=0.5,w1=w2=w3=0.5
∇ w 1 < 1 2 ∗ 1 4 ∗ 1 2 ∗ 1 4 ∗ 1 2 ∗ ∇ o u t = 1 2 7 ∇ o u t \nabla w1< \frac{1}{2} * \frac{1}{4}* \frac{1}{2}* \frac{1}{4}*\frac{1}{2}*\nabla out = \frac{1}{2^7} \nabla out ∇w1<21∗41∗21∗41∗21∗∇out=271∇out
当权重初始过小或使用易饱和神经元(sigmoid,tanh,) sigmoid在y=0,1处梯度接近0,而无法更新参数,时神经网络在反向传播时也会呈现指数倍缩小,产生“消失”现象。
1.2 梯度爆炸
假设 X 2 = 2 , w 1 = w 2 = w 3 = 2 X2=2,w1=w2=w3=2 X2=2,w1=w2=w3=2
$\nabla w1 = f’{a}2f‘{a}*x2\nabla out = 23f’(a)2 \nabla out $
当权重初始过大时,梯度神经网络在反向传播时也会呈现指数倍放大,产生“爆炸”现象。
1.3 解决梯度消失或者梯度爆炸的经验
2. nn.Sequential
nn.Sequential是一个有序的容器,其中传入的是构造器类(各种用来处理input的类),最终input会被Sequential中的构造器类依次执行
例如:
layer = nn.Sequential(
nn.Linear(input_dim, n_hidden_1),
nn.ReLU(True), #inplace=False 是否对输入进行就地修改,默认为False
nn.Linear(n_hidden_1, n_hidden_2),
nn.ReLU(True),
nn.Linear(n_hidden_2, output_dim) # 最后一层不需要添加激活函数
)
在上述就够中,可以直接调用layer(x),得到输出
x的被执行顺序就是Sequential中定义的顺序:
- 被隐层1执行,形状变为[batch_size,n_hidden_1]
- 被relu执行,形状不变
- 被隐层2执行,形状变为[batch_size,n_hidden_2]
- 被relu执行,形状不变
- 被最后一层执行,形状变为[batch_size,output_dim]
3. nn.BatchNorm1d
batch normalization 翻译成中文就是批规范化,即在每个batch训练的过程中,对参数进行归一化的处理,从而达到加快训练速度的效果。
以sigmoid激活函数为例,他在反向传播的过程中,在值为0,1的时候,梯度接近0,导致参数被更新的幅度很小,训练速度慢。但是如果对数据进行归一化之后,就会尽可能的把数据拉倒[0-1]的范围,从而让参数更新的幅度变大,提高训练的速度。
batchNorm一般会放到激活函数之后,即对输入进行激活处理之后再进入batchNorm
layer = nn.Sequential(
nn.Linear(input_dim, n_hidden_1),
nn.ReLU(True),
nn.BatchNorm1d(n_hidden_1)
nn.Linear(n_hidden_1, n_hidden_2),
nn.ReLU(True),
nn.BatchNorm1d(n_hidden_2)
nn.Linear(n_hidden_2, output_dim)
)
4. nn.Dropout
dropout在前面已经介绍过,可以理解为对参数的随机失活
- 增加模型的稳健性
- 可以解决过拟合的问题(增加模型的泛化能力)
- 可以理解为训练后的模型是多个模型的组合之后的结果,类似随机森林。
layer = nn.Sequential(
nn.Linear(input_dim, n_hidden_1),
nn.ReLU(True),
nn.BatchNorm1d(n_hidden_1)
nn.Dropout(0.3) #0.3 为dropout的比例,默认值为0.5
nn.Linear(n_hidden_1, n_hidden_2),
nn.ReLU(True),
nn.BatchNorm1d(n_hidden_2)
nn.Dropout(0.3)
nn.Linear(n_hidden_2, output_dim)
)