【Matlab】智能优化算法_猎豹优化算法CO)
【Matlab】智能优化算法_猎豹优化算法CO
- 1.背景介绍
- 2.数学模型
-
- 2.1 搜索策略
- 2.2 坐等策略
- 2.3 攻击策略
- 2.4 假设
- 3.文件结构
- 4.伪代码
- 5.详细代码及注释
-
- 5.1 CO.m
- 5.2 CO_VectorBased.m
- 5.3 Get_Functions_details.m
- 6.运行结果
- 7.参考文献
1.背景介绍
猎豹(Achinonyx jubatus)是生活在伊朗和非洲中部地区的主要猫科动物品种和速度最快的陆地动物。猎豹的时速可达120公里以上。猎豹的敏捷和速度是它们的身体特征,如长尾巴、细长的腿、轻巧和灵活的脊柱。猎豹是一种行动敏捷的动物,能隐蔽行动,捕食时能快速返回,并有特殊的斑点皮毛;但是,这些视觉捕食者不能长时间保持其高速行动。因此,追逐时间必须少于半分钟。
此外,猎豹在捕获猎物后,仅在三步之内速度就会从93公里/小时或58英里/小时大幅下降到23公里/小时或14英里/小时。由于猎豹在保持速度方面的上述限制,它们在小树枝或山丘上停留后会精确地观察环境以识别猎物。此外,这些大型猫科动物由于其特殊的外衣,可以毫不费力地混入高而干燥的草丛中。
这些掠食者通常捕食瞪羚,特别是汤姆逊瞪羚、黑斑羚、羚羊、野兔、鸟类、啮齿类动物和更多神话般的群居动物的幼崽。首先,它们以蹲伏的姿势缓慢地向猎物移动,以便隐蔽并达到最小距离,然后隐蔽地停下来,等待猎物接近捕食者。这是因为如果猎物观察到捕食者,它们就会停止狩猎。所提到的最小距离差不多是60-70米或200-230英尺;但是,如果它们不能保持适当的隐蔽,则确定为200米或660英尺。具体来说,追逐持续时间为60秒,平均距离为173米或568英尺至559米或1834英尺。然后,猎物的臀部被猎豹的前爪拍打后失去平衡,最后,捕食者使用过大的力量将猎物压倒并翻转,这使得猎物试图逃跑。猎豹肌肉发达的尾巴来回运动也有助于它们实现急转弯。一般来说,猎捕远离族群或不太谨慎的动物要容易得多。需要注意的是,捕食的决定因素有很多,包括动物的成熟度、性别、捕食者的数量以及猎物的粗心程度。此外,联盟或有幼崽的母兽往往能成功捕猎更多的巨型动物。
根据生物学研究发现,猎豹的脊柱非常灵活,尾巴很长,这使它们能够保持身体平衡。此外,它们的肩胛骨与锁骨分离,有利于肩部的活动。前面提到的所有特征使这些大型猫科动物被认为是出色的捕食者;然而,并非所有的捕食都是成功的。
2.数学模型
当猎豹巡逻或扫描周围环境时,有可能发现猎物。看到猎物后,猎豹可能会坐在原地等待猎物靠近,然后开始攻击。攻击模式包括冲撞和捕捉阶段。猎豹可能会因能量限制、猎物快速逃离等原因而放弃狩猎。然后,它们可能会回家休息并开始新的狩猎。通过评估猎物、猎物状况、猎物区域和距离,猎豹可以选择其中一种策略,如图1所示。总之,CO算法的基础是在狩猎期间(迭代)智能地利用这些狩猎策略。
- 搜索:猎豹需要在其领地(搜索空间)或周围地区进行搜索,包括扫描或主动搜索,以找到猎物。
- 坐以待毙:猎豹发现猎物后,如果情况不合适,猎豹可能会坐下来等待猎物靠近或位置更好;
- 攻击:这种策略有两个基本步骤:
- 冲撞:当猎豹决定攻击时,它们会以最快的速度冲向猎物。
- 捕捉:猎豹利用速度和灵活性通过接近猎物来捕获猎物。
- 离开猎物回家: 这种策略考虑了两种情况。(1)如果猎豹未能成功捕猎到猎物,它应该改变位置或返回自己的领地。(2)如果猎豹在一段时间内没有成功地捕猎到猎物,它可以改变位置到最后发现的猎物周围进行搜索。
2.1 搜索策略
猎豹寻找猎物的方式有两种:一种是坐着或站着扫描环境,另一种是在周围积极巡逻。当猎物密集且在平原上行走时,扫描模式更适合。另一方面,如果猎物分散而活跃,选择比扫描模式需要更多能量的主动模式会更好。因此,在狩猎期间,根据猎物的状况、区域的覆盖范围以及猎豹自身的状况,猎豹可能会选择这两种搜索模式的连锁搜索。为了对猎豹的这种搜索策略进行数学建模,让Xt i,j表示猎豹i(i = 1, 2, …, n)在排列j(j = 1, 2, …, D)中的当前位置,其中n是猎豹种群的数量,D是优化问题的维数。事实上,每只猎豹在面对不同猎物时都会遇到不同的情况。每只猎物都是一个与最佳解相对应的决策变量的位置,而猎豹的状态(其他安排)则构建了一个种群。
然后,根据猎豹i的当前位置和任意步长,提出以下随机搜索方程,用于更新猎豹i在每个排列中的新位置:
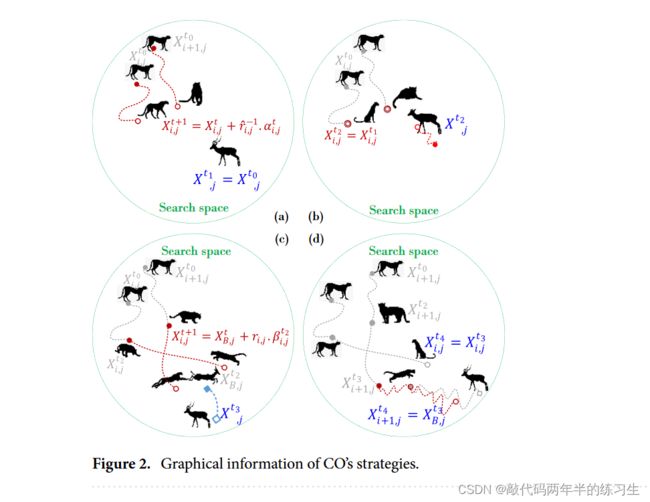
其中,Xt+1 i,j和Xt i,j分别为猎豹i在排列j中的下一个位置和当前位置。索引t表示当前狩猎时间,T为最大狩猎时间长度。ˆ r-1 i,j和αt i,j分别为猎豹i在布置j中的随机化参数和步长。第二项为随机化项,其中随机化参数ˆ ri,j为标准正态分布中的正态分布随机数。在大多数情况下,步长αt i,j > 0可以设置为0.001 × t/T,因为猎豹的搜索速度较慢。在遇到其他猎手(敌人)时,猎豹可能会迅速逃跑并改变方向。为了反映猎豹的这种行为以及近/远目的地搜索模式,这里使用随机数ˆ r-1 i,j来表示每只猎豹在不同狩猎期的行为。在某些情况下,αt i,j可以根据猎豹i和它的邻居或首领之间的距离来调整。每组猎豹中一只猎豹(被命名为首领)的位置是通过假设αt i,j等于0.001×t/T乘以最大步长来更新的(在这里,我们认为它是基于可变的限制,即上限减去下限)。对于其他成员,每只猎豹排列中的αt i,j是通过乘以猎豹i的位置与随机选择的猎豹之间的距离来计算的。图2a说明了搜索策略。
领头羊和猎物(即本文中的最佳解决方案)之间存在一定距离。因此,通过改变最佳方案中的一些变量,根据猎物的位置来选择首领的位置。可以预计,除非狩猎时间结束,否则领头羊和猎物的距离会更近,从而更新领头羊位置。值得注意的是,猎豹的步长是完全随机的,CO会考虑这一点。因此,CO可以利用任何随机化参数和随机步长,即ˆr-1 i,j和αt i,j,有效地正确解决优化问题。
2.2 坐等策略
在搜索模式下,猎物可能会暴露在猎豹的视野中。在这种情况下,猎豹的一举一动都可能让猎物察觉到它的存在,从而导致猎物逃跑。为了避免这种担忧,猎豹可能会决定伏击(趴在地上或躲在灌木丛中),以足够接近猎物。因此,在这种模式下,猎豹会留在自己的位置上等待猎物靠近(见图2b)。这种行为可模拟如下
其中Xt+1 i,j和Xt i,j分别为猎豹i在排列j中的更新位置和当前位置。该策略要求CO算法不要同时改变每组中的所有猎豹,以提高狩猎成功率(找到更好的解决方案),从而避免过早收敛。
2.3 攻击策略
猎豹利用两个关键因素攻击猎物:速度和灵活性。当猎豹决定发动攻击时,它会全速冲向猎物。过了一会儿,猎物发现了猎豹的攻击并开始逃跑。如图2c所示,猎豹在拦截路径上用敏锐的眼睛迅速追赶猎物。换句话说,猎豹跟踪猎物的位置并调整其运动方向,以便在某一点阻挡猎物的去路。如图2d所示,猎豹的下一个位置靠近猎物的上一个位置。另外,如图2d所示,这只猎豹可能没有参与完全符合猎豹自然狩猎的攻击策略。猎豹在这一阶段利用速度和灵活性捕获猎物。在集体狩猎中,每只猎豹都可以根据逃跑的猎物和领头猎豹或邻近猎豹的位置调整自己的位置。简单地说,猎豹的这些攻击战术在数学上定义如下:
其中,Xt B,j 是猎物在布置 j 中的当前位置,换句话说,它是种群的当前最佳位置。Xt B,j在(3)中使用是因为在攻击模式下,猎豹利用最大速度的冲刺策略帮助它们在短时间内尽可能接近猎物的位置。因此,本文根据猎物的当前位置计算第i只猎豹在攻击模式下的新位置。在第二项中,转向因子βt i,j反映了捕猎模式下猎豹之间或猎豹与首领之间的相互作用。在数学上,这个因子可以定义为邻近猎豹的位置Xt k,j (k = i )与第i只猎豹的位置Xt i,j之间的差值。在本文中,转弯因子ˇ ri,j 是一个随机数,等于|ri,j|exp(ri,j/2)sin(2π ri,j )。该系数反映了猎豹在捕捉模式下的急转弯。
2.4 假设
根据猎豹的出没行为,在所提出的CO算法中考虑了以下假设:
- 猎豹种群的每一行都被模拟为处于不同状态的猎豹。每一列代表猎豹对猎物的特定安排(每个决策变量的最佳方案)。换句话说,猎豹跟随猎物(变量的最佳点)。为了找到最佳的最优解,猎豹需要在每个排列中成功捕获猎物。每只猎豹的表现由该猎豹在所有排列中的适应度函数值来评估。猎豹的表现越好,表示捕猎成功的概率越高。
- 在真实的群体狩猎过程中,所有猎豹的反应都与其他猎豹不同。事实上,在每种安排中,一只猎豹可能处于攻击模式,而其他猎豹可能处于搜索、坐等和攻击模式中的一种。此外,猎豹的能量与猎物无关。除了使用随机参数ˆr-1 i,j和ˇri,j外,将每个决策变量建模为猎豹的排列,即使在一个非常大的演化过程中也能防止过早收敛。这些随机变量可以被认为是猎豹在狩猎过程中的能量来源。在以前的狩猎进化方法中,这两个关键思想被忽略了,严重影响了优化性能。在攻击策略中,猎豹的方向取决于猎物,但在搜索策略中猎豹的运动完全是随机行为。
- 假设猎豹在搜索或攻击策略中的行为是完全随机的,如图2中红色虚线所示,但在冲撞和捕捉模式中,猎豹的方向是急剧变化的,如图2d中最后一个动作所示。随机化参数ˆ ri,j和转弯因子ˇ ri,j模拟了这些随机运动。用完全随机变量改变步长αt i,j和相互作用系数βt i,j也可以得到合适的优化过程。这些都证实了狩猎过程是精确建模的。
- 在狩猎过程中,搜索或攻击策略是随机部署的,但随着时间的推移,由于猎豹能量水平的降低,搜索策略变得更有可能。在某些情况下,前几步采用搜索策略,而在t值较大时采用攻击策略以获得更好的解。假设r2和r3为[0,1]中的均匀随机数。如果r2≥r3,则选择坐等策略;否则,根据随机值H=e2(1-t/T)(2r1-1)(其中r1为[0,1]中的均匀随机数)选择搜索策略或攻击策略中的一种。通过调整r3,可以控制 "坐等 "策略与其他两种策略之间的切换率。例如,根据我们的经验,如果目标函数对某些决策变量的变化过于敏感(这可能反映了猎物对猎豹移动的敏感性),r3的值可以选择小的随机数。这种情况增加了猎豹选择的坐等模式,降低了决策变量的变化率。因此,狩猎(找到更好的解决方案)的成功概率增加。由于能量限制,H函数中t的增加会降低猎豹选择攻击策略的概率。尽管如此,该概率并不为零,这完全是受猎豹行为的启发。为此,如果H≥r4,则选择攻击模式,否则执行搜索模式。r4为0-3之间的随机数。在这里,r4值越大,开发阶段越突出,而r4值越小,探索阶段越突出。
- 在CO算法中,扫描策略和坐等策略具有相同的含义,表示猎豹(搜索代理)在狩猎期间没有移动。6. 6.如果领头猎豹在某次连续的狩猎过程中狩猎失败,则随机选择一只猎豹的位置变为上次成功狩猎的位置(即猎物位置)。在此算法中,保持猎物在小种群中的位置加强了探索阶段。7. 由于能量的限制,每组猎豹的狩猎时间都是有限的。因此,如果一个猎豹群在一个狩猎周期内未能成功狩猎,当前的猎物将被丢弃,猎豹群将回到其原地(本文中的初始位置)休息,然后开始新的狩猎。事实上,如果一群猎豹的能量(用狩猎时间来模拟)减少,而首领的位置不变,它们就会回家。在这种情况下,领头羊的位置也会被更新。采用这种策略可以避免陷入局部最优解。8. 在每次迭代中,部分成员参与进化过程。
3.文件结构
CO.m % 猎豹优化算法
CO_VectorBased.m % 主函数
Get_Functions_details.m % 函数细节
4.伪代码
5.详细代码及注释
5.1 CO.m
clc;
clear all;
close all;
%% Problem Definition
f_name=['F1'];
tic
for fnm = 1 % Test functions
for run = 1 : 1
%% Problem definition (Algorithm 1, L#1)
if fnm <= 9
Function_name = f_name(fnm,:);
else
Function_name = f_name1(fnm-9,:);
end
[lb,ub,D,fobj] = Get_Functions_details(Function_name); % The shifted functions' information
D = 100; % Number of Decision Variables
if length(lb) == 1
ub = ub.*ones(1,D); % Lower Bound of Decision Variables
lb = lb.*ones(1,D); % Upper Bound of Decision Variables
end
n = 6; % Population Size
m = 2; % Number of search agenets in a group
%% Generate initial population of cheetahs (Algorithm 1, L#2)
empty_individual.Position = [];
empty_individual.Cost = [];
BestSol.Cost = inf;
pop = repmat(empty_individual,n,1);
for i=1:n
pop(i).Position = lb+rand(1,D).*(ub-lb);
pop(i).Cost = fobj(pop(i).Position);
if pop(i).Cost < BestSol.Cost
BestSol = pop(i); % Initial leader position
end
end
%% Initialization (Algorithm 1, L#3)
pop1 = pop; % Population's initial home position
BestCost = []; % Leader fittnes value in a current hunting period
X_best = BestSol; % Prey solution sofar
Globest = BestCost; % Prey fittnes value sofar
%% Initial parameters
t = 0; % Hunting time counter (Algorithm 1, L#4)
it = 1; % Iteration counter(Algorithm 1, L#5)
MaxIt = D*10000; % Maximum number of iterations (Algorithm 1, L#6)
T = ceil(D/10)*60; % Hunting time (Algorithm 1, L#7)
FEs = 0; % Counter for function evaluations (FEs)
%% CO Main Loop
while FEs <= MaxIt % Algorithm 1, L#8
% m = 1+randi (ceil(n/2));
i0 = randi(n,1,m); % select a random member of cheetahs (Algorithm 1, L#9)
for k = 1 : m % Algorithm 1, L#10
i = i0(k);
% neighbor agent selection (Algorithm 1, L#11)
if k == length(i0)
a = i0(k-1);
else
a = i0(k+1);
end
X = pop(i).Position; % The current position of i-th cheetah
X1 = pop(a).Position; % The neighbor position
Xb = BestSol.Position; % The leader position
Xbest = X_best.Position;% The pery position
kk=0;
% Uncomment the follwing statements, it may improve the performance of CO
if i<=2 && t>2 && t>ceil(0.2*T+1) && abs(BestCost(t-2)-BestCost(t-ceil(0.2*T+1)))<=0.0001*Globest(t-1)
X = X_best.Position;
kk = 0;
elseif i == 3
X = BestSol.Position;
kk = -0.1*rand*t/T;
else
kk = 0.25;
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
if mod(it,100)==0 || it==1
xd = randperm(numel(X));
end
Z = X;
%% Algorithm 1, L#12
for j = xd % select arbitrary set of arrangements
%% Algorithm 1, L#13
r_Hat = randn; % Randomization paameter, Equation (1)
r1 = rand;
if k == 1 % The leader's step length (it is assumed that k==1 is associated to the leade number)
alpha = 0.0001*t/T.*(ub(j)-lb(j)); % Step length, Equation (1) %This can be updated by desired equation
else % The members' step length
alpha = 0.0001*t/T*abs(Xb(j)-X(j))+0.001.*round(double(rand>0.9));%member step length, Equation (1)%This can be updated by desired equation
end
r = randn;
r_Check = abs(r).^exp(r/2).*sin(2*pi*r); % Turning factor, Equation (3)%This can be updated by desired equation
beta = X1(j)-X(j); % Interaction factor, Equation (3)
h0 = exp(2-2*t/T);
H = abs(2*r1*h0-h0);
%% Algorithm 1, L#14
r2 = rand;
r3 = kk+rand;
%% Strategy selection mechanism
if r2 <= r3 % Algorithm 1, L#15
r4 = 3*rand; % Algorithm 1, L#16
if H > r4 % Algorithm 1, L#17
Z(j) = X(j)+r_Hat.^-1.*alpha; % Search, Equation(1) (Algorithm 1, L#18)
else
Z(j) = Xbest(j)+r_Check.*beta; % Attack, Equation(3) (Algorithm 1, L#20)
end
else
Z(j) = X(j); % Sit&wait, Equation(2) (Algorithm 1, L#23)
end
end
%% Update the solutions of member i (Algorithm 1, L#26)
% Check the limits
xx1=find(Z<lb);
Z(xx1)=lb(xx1)+rand(1,numel(xx1)).*(ub(xx1)-lb(xx1));
xx1=find(Z>ub);
Z(xx1)=lb(xx1)+rand(1,numel(xx1)).*(ub(xx1)-lb(xx1));
% Evaluate the new position
NewSol.Position = Z;
NewSol.Cost = fobj(NewSol.Position);
if NewSol.Cost < pop(i).Cost
pop(i) = NewSol;
if pop(i).Cost < BestSol.Cost
BestSol = pop(i);
end
end
FEs = FEs+1;
end
t = t+1; % (Algorithm 1, L#28)
%% Leave the prey and go back home (Algorithm 1, L#29)
if t>T && t-round(T)-1>=1 && t>2
if abs(BestCost(t-1)-BestCost(t-round(T)-1))<=abs(0.01*BestCost(t-1))
% Change the leader position (Algorithm 1, L#30)
best = X_best.Position;
j0=randi(D,1,ceil(D/10*rand));
best(j0) = lb(j0)+rand(1,length(j0)).*(ub(j0)-lb(j0));
BestSol.Cost = fobj(best);
BestSol.Position = best; % Leader's new position
FEs = FEs+1;
i0 = randi(n,1,round(1*n));
% Go back home, (Algorithm 1, L#30)
pop(i0(n-m+1:n)) = pop1(i0(1:m)); % Some members back their initial positions
pop(i) = X_best; % Substitude the member i by the prey (Algorithm 1, L#31)
t = 1; % Reset the hunting time (Algorithm 1, L#32)
end
end
it = it +1; % Algorithm 1, L#34
%% Update the prey (global best) position (Algorithm 1, L#35)
if BestSol.Cost<X_best.Cost
X_best=BestSol;
end
BestCost(t)=BestSol.Cost;
Globest(1,t)=X_best.Cost;
%% Display
if mod(it,500)==0
disp([' FEs>> ' num2str(FEs) ' BestCost = ' num2str(Globest(t))]);
end
end
% fit(run) = Globest(end) ;
% mean_f = mean (fit);
% std_f = std (fit);
% clc
end
end
toc
5.2 CO_VectorBased.m
clc;
clear all;
close all;
%% Problem Definition
f_name=['F1'];
tic
for fnm = 4 % Test functions
for run = 1 : 1
%% Problem definition (Algorithm 1, L#1)
if fnm <= 9
Function_name = f_name(fnm,:);
else
Function_name = f_name1(fnm-9,:);
end
[lb,ub,D,fobj] = Get_Functions_details(Function_name); % The shifted functions' information
D = 100; % Number of Decision Variables
if length(lb) == 1
ub = ub.*ones(1,D); % Lower Bound of Decision Variables
lb = lb.*ones(1,D); % Upper Bound of Decision Variables
end
n = 6; % Population Size
m = 2; % Number of search agenets in a group
%% Generate initial population of cheetahs (Algorithm 1, L#2)
empty_individual.Position = [];
empty_individual.Cost = [];
BestSol.Cost = inf;
pop = repmat(empty_individual,n,1);
for i=1:n
pop(i).Position = lb+rand(1,D).*(ub-lb);
pop(i).Cost = fobj(pop(i).Position);
if pop(i).Cost < BestSol.Cost
BestSol = pop(i); % Initial leader position
end
end
%% Initialization (Algorithm 1, L#3)
pop1 = pop; % Population's initial home position
BestCost = []; % Leader fittnes value in a current hunting period
X_best = BestSol; % Prey solution sofar
Globest = BestCost; % Prey fittnes value sofar
%% Initial parameters
t = 0; % Hunting time counter (Algorithm 1, L#4)
it = 1; % Iteration counter(Algorithm 1, L#5)
MaxIt = D*10000; % Maximum number of iterations (Algorithm 1, L#6)
T = ceil(D/10)*60; % Hunting time (Algorithm 1, L#7)
FEs = 0; % Counter for function evaluations (FEs)
%% CO Main Loop
while FEs <= MaxIt % Algorithm 1, L#8
% m = 1+randi (ceil(n/2));
i0 = randi(n,1,m); % select a random member of cheetahs (Algorithm 1, L#9)
for k = 1 : m % Algorithm 1, L#10
i = i0(k);
% neighbor agent selection (Algorithm 1, L#11)
if k == length(i0)
a = i0(k-1);
else
a = i0(k+1);
end
X = pop(i).Position; % The current position of i-th cheetah
X1 = pop(a).Position; % The neighbor position
Xb = BestSol.Position; % The leader position
Xbest = X_best.Position;% The pery position
kk=0;
% Uncomment the follwing statements, it may improve the performance of CO
if i<=2 && t>2 && t>ceil(0.2*T+1) && abs(BestCost(t-2)-BestCost(t-ceil(0.2*T+1)))<=0.0001*Globest(t-1)
X = X_best.Position;
kk = 0;
elseif i == 3
X = BestSol.Position;
kk = -0.1*rand*t/T;
else
kk = 0.25;
end
Z = X;
%% Algorithm 1, L#12
% for j = xd % select arbitrary set of arrangements
%% Algorithm 1, L#13
r_Hat = randn(1,D); % Randomization paameter, Equation (1)
r1 = rand(1,D);
if k == 1 % The leader's step length (it is assumed that k==1 is associated to the leade number)
alpha = 0.0001*t/T.*(ub-lb); % Step length, Equation (1)%This can be updated by desired equation
else % The members' step length
alpha = 0.0001*t/T*abs(Xb-X)+0.001.*round(double(rand(1,D)>0.6));%member step length, Equation (1)%This can be updated by desired equation
% alpha = 0.0001*t/T*abs(Xb-X)+0.001.*round(double(rand>0.9));%member step length, Equation (1)%This can be updated by desired equation
end
r = randn(1,D);
r_Check = abs(r).^exp(r./2).*sin(2.*pi.*r); % Turning factor, Equation (3)%This can be updated by desired equation
beta = X1-X; % Interaction factor, Equation (3)
h0 = exp(2-2*t/T);
H = abs(2.*r1.*h0-h0);
%% Algorithm 1, L#14
r2 = rand(1,D);
r3 = kk+rand(1,D);
%% Strategy selection mechanism
r4 = 3*rand(1,D); % Algorithm 1, L#16
f1=find( H > r4); % Algorithm 1, L#17
Z(f1) = X(f1)+r_Hat(f1).^-1.*alpha(f1); % Search, Equation(1) (Algorithm 1, L#18)
f1=find( H <= r4);
Z(f1) = Xbest(f1)+r_Check(f1).*beta(f1); % Attack, Equation(3) (Algorithm 1, L#20)
f1=find( r2 > r3);
Z(f1) = X(f1); % Sit&wait, Equation(2) (Algorithm 1, L#23)
%% Update the solutions of member i (Algorithm 1, L#26)
% Check the limits
xx1=find(Z<lb);
Z(xx1)=lb(xx1)+rand(1,numel(xx1)).*(ub(xx1)-lb(xx1));
xx1=find(Z>ub);
Z(xx1)=lb(xx1)+rand(1,numel(xx1)).*(ub(xx1)-lb(xx1));
% Evaluate the new position
NewSol.Position = Z;
NewSol.Cost = fobj(NewSol.Position);
if NewSol.Cost < pop(i).Cost
pop(i) = NewSol;
if pop(i).Cost < BestSol.Cost
BestSol = pop(i);
end
end
FEs = FEs+1;
end
t = t+1; % (Algorithm 1, L#28)
%% Leave the prey and go back home (Algorithm 1, L#29)
if t>T && t-round(T)-1>=1 && t>2
if abs(BestCost(t-1)-BestCost(t-round(T)-1))<=abs(0.01*BestCost(t-1))
% Change the leader position (Algorithm 1, L#30)
best = X_best.Position;
j0=randi(D,1,ceil(D/10*rand));
best(j0) = lb(j0)+rand(1,length(j0)).*(ub(j0)-lb(j0));
BestSol.Cost = fobj(best);
BestSol.Position = best; % Leader's new position
FEs = FEs+1;
i0 = randi(n,1,round(1*n));
% Go back home, (Algorithm 1, L#30)
pop(i0(n-m+1:n)) = pop1(i0(1:m)); % Some members back their initial positions
pop(i) = X_best; % Substitude the member i by the prey (Algorithm 1, L#31)
t = 1; % Reset the hunting time (Algorithm 1, L#32)
end
end
it = it +1; % Algorithm 1, L#34
%% Update the prey (global best) position (Algorithm 1, L#35)
if BestSol.Cost<X_best.Cost
X_best=BestSol;
end
BestCost(t)=BestSol.Cost;
Globest(1,t)=X_best.Cost;
%% Display
if mod(it,500)==0
disp([' FEs>> ' num2str(FEs) ' BestCost = ' num2str(Globest(t))]);
end
end
% fit(run) = Globest(end) ;
% mean_f = mean (fit);
% std_f = std (fit);
% clc
end
end
toc
5.3 Get_Functions_details.m
function [lb,ub,dim,fobj] = Get_Functions_details(F)
%%% SHIFTED OBJECTIVE FUNCTIONS
switch F
case 'F1'
fobj = @F1;
lb=-100;
ub=100;
dim=100;
end
end
% F1
function o = F1(x)
dim=size(x,2);
x1=[-44,5,42,-68,-41,83,-44,96,-43,21,-58,-60,-14,-71,-91,-30,86,45,54,-70,80,-80,96,87,28,-94,-9,-59,61,46,78,91,84,-98,7,32,-23,-81,-55,-39,-41,-33,16,-4,95,34,-39,-69,-96,-93,57,77,2,-56,85,67,12,-17,-31,-89,8,92,-26,16,99,33,-7,7,25,-55,30,-57,54,66,-13,-8,-87,-28,0,-74,1,43,-68,84,42,53,-79,-82,-44,33,-30,49,-69,-98,69,41,69,99,44,-18,-1,88,-47,28,72,97,95,96,88,42,-66,47,15,-77,60,-60,-73,63,-37,-88,-38,13,27,-72,-77,2,-41,-23,46,59,-88,-77,43,-71,23,79,-81,-54,-69,97,38,-98,38,-3,-53,26,67,-56,59,-79,72,-85,-7,-70,-90,88,-17,15,22,-56,-31,-4,32,-6,94,-95,-77,85,4,99,58,99,-99,35,-12,-5,94,-64,-1,-18,-78,76,83,84,49,-86,-10,-70,61,17,-76,-83,71,6,99,70,2,-56,80,-92,-51,-10,-68,-3,-62,91,46,-39,35,38,-95,-19,8,60,87,22,-37,-74,-40,61,97,82,25,28,57,-68,7,-85,89,-66,12,-29,-61,52,-20,-86,-34,50,-58,68,39,79,34,35,-76,-83,4,-3,-39,-64,-81,94,32,-48,7,-10,-28,-32,-71,-63,-82,-58,-18,54,-88,0,4,35,97,18,55,-37,-73,45,55,-18,-48,6,-66,5,-35,-72,55,53,-82,-13,-83,26,-74,-96,87,19,55,49,24,47,-22,-55,42,-39,13,-49,-72,-50,79,-34,100,41,5,-78,9,-39,49,-31,76,51,-57,-49,68,-63,78,-36,88,18,-39,-57,43,14,94,45,-66,15,-85,89,-55,88,-22,-50,-99,54,54,-54,25,53,-70,53,-52,87,-79,71,-19,59,-10,87,62,11,-66,-39,-98,98,87,-45,-50,-9,21,72,11,40,-23,36,65,-65,-3,-50,100,-8,-51,-20,-96,-7,74,-58,-20,-46,-61,25,-21,-51,-62,64,-73,-69,81,16,-18,-54,45,99,-11,55,57,-57,14,62,38,-74,93,-95,-19,-19,29,29,17,92,-10,-23,-68,87,-30,34,61,58,-13,-1,25,73,57,-42,-20,-58,-58,45,23,4,72,38,-86,16,68,-92,-23,-68,12,26,-1,67,4,-24,41,53,91,-55,-65,-95,-54,2,71,-15,-57,87,67,-36,15,-38,22,48,-88,-9,-53,10,-61,-16,17,-67,84,-18,28,-24,83,29,60,52,-59,-57,-68,-98,65,96,-59,37,-64,-34,-74,66,-54,-5,-84,-20,46,8,91,60,-94,-15,-24,52,89,98,89,54,50,-77,-17,61,-47,55,29,-34,-24,-49,65,75,-95,-94,66,-43,10,23,87,-52,-82,-41,16,-35,63,45,77,-17,-49,-13,57,23,97,-99,36,83,-49,-60,-80,70,14,61,-38,-27,28,46,8,-36,-19,5,-88,-53,-97,52,-16,-6,82,96,18,16,5,-10,95,9,27,-57,73,24,-57,40,32,12,82,92,-20,-51,72,-44,-66,-77,33,73,10,22,-42,85,24,-51,97,45,88,-75,-82,-19,38,-53,43,-85,22,-67,-93,-73,-75,44,2,0,-3,-59,85,31,-23,52,47,63,82,0,-41,24,-23,36,-13,95,46,93,-26,60,21,40,-23,-37,35,64,-65,2,-35,2,-88,30,22,80,100,-15,-54,-90,-85,6,20,-9,-19,-27,30,-51,5,1,88,-70,60,41,79,89,-90,-41,-90,49,25,81,-4,-24,4,52,77,66,58,77,24,21,43,93,93,-54,-54,-64,-94,-13,-34,33,-75,-50,-54,-88,-42,-8,-51,-5,-20,6,-28,-55,90,-30,-1,-92,-99,-47,-74,-27,-70,33,-8,93,-15,-21,26,40,94,-62,-4,-30,32,-35,-80,-94,36,31,-71,79,-87,-83,99,67,3,84,16,63,70,-34,30,-21,4,56,-90,33,30,-4,3,-9,84,70,58,82,6,-79,-39,18,-75,78,54,60,21,7,68,-75,-34,-53,-47,-33,-1,72,24,7,-59,-31,8,-72,-19,96,-7,-78,-99,22,-84,6,79,41,47,-5,-63,51,-76,99,-46,-21,-7,60,-20,-62,31,-47,9,26,68,-63,85,-15,11,-83,33,-91,-74,42,64,-23,-66,49,-62,85,94,66,-26,-58,28,-52,-47,73,26,14,36,80,6,-34,99,93,93,-43,-88,-91,-40,43,-90,49,80,2,-65,0,-90,49,-8,-69,-67,62,-31,-66,-67,-79,29,41,1,61,-32,32,55,-97,59,-66,-35,-26,-98,-59,17,-1,-36,-95,-100,-86,21,7,91,-43,-10,-41,-61,-91,22,68,76,-26,-96,58,29,51,1,-89,98,-74,94,66,-73,94,-19,-71,-79,-71,-26,15,-23,-71,29,40,-22,-39,82,-72,-9,-81,-99,7,-58,83,1,50,-50,84,20,83,8,94,-100,-41,4,24,66,35,-11,-92,71,-91,49,4,-95,83,39,63,-9,15,-2,57,-99,76,20,7,-29,-13,-44,3,-70,-91,-41,-26,18,29,-25,42,61,57,19,-76,2,47,-23,-73,60,46,-50,28,39,59,58,-96,-30,45,-53,45,62,-32,-91,-14,2,-76,-50,23];
x=x-x1(1:length(x));
o=sum((x).^2);
end
6.运行结果
7.参考文献
[1]Amin M A,Mohsen Z,Rasoul A A, et al. The cheetah optimizer: a nature-inspired metaheuristic algorithm for large-scale optimization problems[J]. Scientific Reports,2022,12(1).