基于深度优先算法和A*算法的迷宫游戏开发（Java实现）

先上图

一、实验内容

1、要求：

1）迷宫随机生成
2）系统用A*算法寻路，输出路径
3) 实现基本游戏界面

2、解决问题：

1）如何显示迷宫的图形界面
2）如何生成随机的迷宫
3）怎样移动游戏中走迷宫的“玩家”
4）用A*算法求解迷宫

二、深度优先算法生成迷宫

1、整体思路

1）利用深度遍历的思想。访问到一个节点时，搜索这个节点没有被访问过的相邻节点，选择一个继续做同样的操作，直到没有邻节点为止再回溯到上一个访问的节点，并选择另外的邻节点。
2）这种方案生成的迷宫会有一条明显的主路，这条主路特别长，贯穿大部分区域的路线，同时，迷宫的路线一般比较扭曲。这种采用深度优先算法（递归回溯算法）生成的迷宫称之为“主路扭曲型”迷宫。

2、步骤

（1）把数组地图初始化为如下结构。选择一个靠近边缘的1作为起点，在它的周围随机找另一个黄色的1（这里的“周围”指的是上下左右4个方向）。找到就把他们联通，并且把两个1之间的0（灰色墙）也变成通路，这里用红色来表示。

（2）选择一个靠近边缘的1作为起点，在它的周围随机找另一个黄色的1（这里的“周围”指的是上下左右4个方向）。找到就把他们联通，并且把两个1之间的0（灰色墙）也变成通路，这里用红色来表示。

（3）把上一步”终点”的格子作为新的一个“起点”格子，不断循环第2步的过程……
直到，找不到周围有黄色的1，就回溯，回到之前的位置，看看周围是否有黄色的1，如果有，就按照2步骤，不断将黄色1变联通，接下来就是不停地重复上面的步骤，找到就联通，找不到就往回走。

（4）遍历完所有的点即可生成一个迷宫，然后再选择出口与入口，一个完整的迷宫就形成了。

三、A*算法走迷宫

1、算法概述

在计算机科学中，A*算法作为Dijkstra（迪杰斯特拉）算法的扩展，是一种静态路网中求解最短路径有效的直接搜索方法，因其高效性被广泛应用于寻路及图的遍历中。

搜索区域（The Search Area）：搜索区域被划分为简单的二维数组，数组每个元素对应一个结点。

开放列表（Open List）:将寻路过程中待检测的结点存放于Open List中，而已检测过的结点则存放于Close List中。

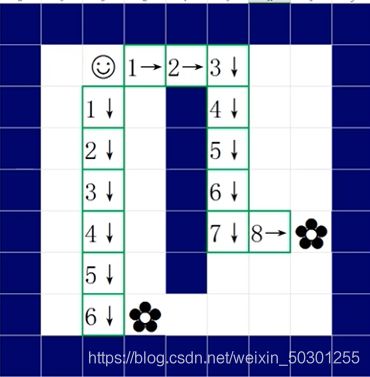
路径排序（Path Sorting）：下一步怎么移动由以下公式确定；F(n)=G+H。F(n)为估价函数，G代表的是从初始位置Start沿着已生成的路径到指定待检测结点移动开销。H表示待检测结点到目标节点B的估计移动开销。

启发函数（Heuristics Function）: H为启发函数，可以看作是一种试探，由于在找到唯一路径前，不确定在前面会出现什么障碍物，因此用了一种计算H的算法，具体可以根据实际情况决定。为了简化问题，H采用的是传统的曼哈顿距离，也就是横纵向走的距离之和。

2、算法流程

重复以下步骤，直到遍历到终点 End：
1）选取当前 open 列表中评价值 F 最小的节点，将这个节点称为 S；
2）将 S 从 open列表移除，然后添加 S 到 closed 列表中； 3）对于与 S 相邻的每一块可移动的相邻节点 T：

如果 T 在 closed列表中，忽略；
如果 T 不在 open 列表中，添加它然后计算它的 F值；
如果 T 已经在 open 列表中，当我们从 S 到达 T时：检查是否能得到更小的 F 值，
如果是，更新它的 F 值和它的前继(parent = S)。

3、算法原理

（1）两个列表:

open： 一个记录下所有被考虑来寻找最短路径的方块
closed： 一个记录下不会再被考虑的方块

（2) 路径增量 ： F(n)=G+H

G:是从开始点A到当前方块的移动量。所以从开始点A到相邻小方块的移动量为1，该 值会随着离开始点越来越远而增大。

H:是从当前方块到目标点(我们把它称为点B，代表小花! )的移动量估算值。这个 常被称为探视，因为我们不确定移动量是多少，只是一-个估算值。
为了让它更简单，我们将使用“曼哈顿距离方法”(也叫“曼哈顿长”或者“城市街区距离”)，它只是计算出距离点B，剩下的水平和垂直的方块数量，略去了障碍物或者不同陆地类型的数量。

(3)找到最短路径:

重复之前的步骤。当目标方块在open列表中，即找到路径，
然后回溯，计算出最终的路径!

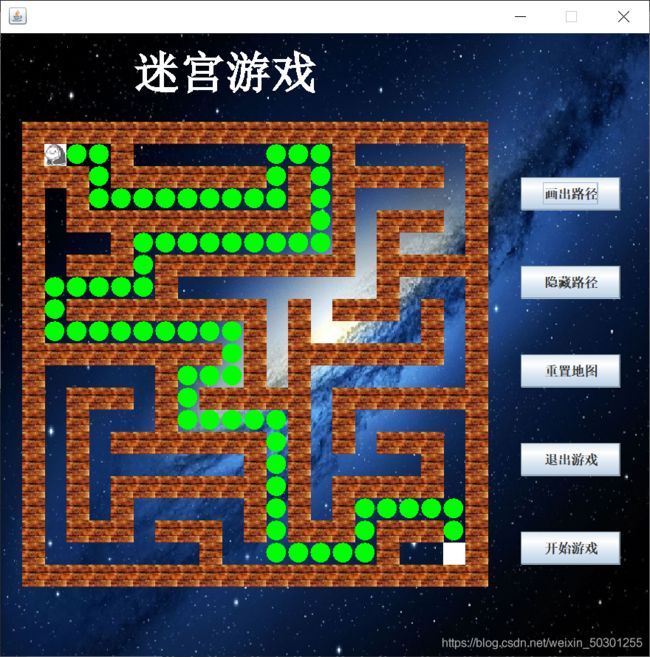
四、结果测试

1、视频演示：

迷宫游戏演示

2、界面：

五、源代码

1、类结构和文件结构

2、图片链接

链接: https://pan.baidu.com/s/1GEWiuwxf1i99Tck3sshZ8g
提取码: mvda

3、完整源代码

（1）Test类

package Maez;
import java.awt.Toolkit;
import javax.swing.JFrame;
public class Test {
    public static void main(String[] args) {	
	JFrame frame = new JFrame();//新建窗口
	int width = Toolkit.getDefaultToolkit().getScreenSize().width;// 取得屏幕宽度
	int height = Toolkit.getDefaultToolkit().getScreenSize().height;// 取得屏幕高度
	frame.setSize(600, 600);// 设置窗体大小
	frame.setLocation((width - 600) / 2, (height - 600) / 2);// 设置窗体出现大小
	frame.setResizable(false);// 设置窗体大小不可变
	frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);// 设置窗体关闭方式
	frame.add(new Panel());
	frame.setFocusable(true);//为屏幕添加焦点	
	frame.setVisible(true);// 设置窗体可视
	frame.requestFocus();
    }
}

（2）Panel类

package Maez;
import java.awt.Color;
import java.awt.Font;
import java.awt.Graphics;
import java.awt.event.KeyEvent;
import java.awt.event.KeyListener;
import java.awt.event.MouseEvent;
import java.awt.event.MouseListener;
import java.awt.image.BufferedImage;
import java.io.File;
import java.io.IOException;
import javax.imageio.ImageIO;
import javax.swing.JButton;
import javax.swing.JPanel;

public class Panel extends JPanel implements MouseListener, KeyListener{

    Maze M = new Maze();//定义一个Maze类对象，生成地图
    AStart A = new AStart();//定义一个AStart类，画出迷宫路径
    
    private JPanel jp = new JPanel();
    private JButton answer = new JButton("画出路径");
    private JButton hide = new JButton("隐藏路径");
    private JButton reset = new JButton("重置地图");
    private JButton exit = new JButton("退出游戏");
    private JButton start = new JButton("开始游戏");
    BufferedImage wall = null;
    BufferedImage bj = null;
    BufferedImage victory = null;
    BufferedImage my = null;

    int myx = 1;// 定义角色横坐标并初始化
    int myy = 1;// 定义角色纵坐标
    int endx;// 定义终点横纵坐标
    int endy;
    boolean isStarted = false;
    boolean isVictory = false;
    boolean ans = false;// 用于显示路径

    public Panel() {
	this.setName("迷宫");// 设置标题
	this.setLayout(null);
	answer.setBounds(470, 130, 90, 30);
	hide.setBounds(470, 210, 90, 30);
	reset.setBounds(470, 290, 90, 30);
	exit.setBounds(470, 370, 90, 30);
	start.setBounds(470, 450, 90, 30);
	answer.addMouseListener(this);
	hide.addMouseListener(this);
	reset.addMouseListener(this);
	exit.addMouseListener(this);
	start.addMouseListener(this);
	start.addKeyListener(this);
	this.add(jp);
	this.add(start);
	this.add(answer);
	this.add(hide);
	this.add(reset);
	this.add(exit);

	try {
	    bj = ImageIO.read(new File("images/bj.jpg"));// 放窗口背景图片	 
	    victory=ImageIO.read(new File("images/victory.png"));
	    wall = ImageIO.read(new File("images/wall.jpg"));// 放墙的图片
	    my = ImageIO.read(new File("images/my.png"));// 放墙的图片
	} catch (IOException e) {
	    e.printStackTrace();
	}
    }

    // 画组件
    public void paintComponent(Graphics g) {
	super.paintComponent(g);		
	g.fillRect(20, 80, 420, 420);
	g.drawImage(bj, 0, 0, this);
	g.setColor(Color.white);
	g.setFont(new Font("华文行楷", Font.BOLD, 40));	
	g.drawString("迷宫游戏", 120, 50);
	
	// 画迷宫
	for (int i = 0; i < M.LabId.length; i++) {
	    for (int j = 0; j < M.LabId[0].length; j++) {
		if (M.LabId[i][j] == 0) {
		    g.drawImage(wall, 20 + i * 20, 80 + j * 20, this);
		}
	    }
	}

	// 画A*路径
	if (ans) {
	    g.setColor(Color.green);
	    for (int i = 0; i < A.NODES.length; i++) {
		for (int j = 0; j < A.NODES[0].length; j++) {
		    if (A.NODES[i][j] == 2) {
			g.fillOval(20 + 20 * i, 80 + 20 * j, 18, 18);
		    }
		}
	    }
	}
	
	g.setColor(Color.white);
	g.fillRect(40, 100, 20, 20);// 画起点
	g.fillRect(400, 460, 20, 20);// 画终点
	g.drawImage(my, 20 + 20 * myx, 80 + 20 * myy, this);// 画角色

	// 判断是否到达终点
	if (this.myx ==19 && this.myy ==19) {
	    isVictory = true;	    
	}

	// 画游戏胜利界面
	if (isVictory) {
	    g.drawImage(victory, 60,180, this);// 画角色	   
	}
    }

    // 鼠标监听
    @Override
    public void mouseClicked(MouseEvent e) {
	if (e.getSource().equals(answer)) {
	    ans = true;
	    isVictory=false;
	}
	if (e.getSource().equals(hide)) {
	    ans = false;
	    isVictory=false;
	}
	if (e.getSource().equals(reset)) {
	    ans = false;
	    isVictory=false;
	    myx = 1;
	    myy = 1;
	    new Panel();
	}
	if (e.getSource().equals(exit)) {
	    System.exit(0);
	}
	if (e.getSource().equals(start)) {
	    ans = false;
	    isVictory=false;
	    myx = 1;// 开始游戏，角色从起点开始出发
	    myy = 1;	   
	}
	repaint();
    }

    // 键盘监听
    @Override
    public void keyTyped(KeyEvent e) {
    }
    @Override
    public void keyPressed(KeyEvent e) {
	int k = e.getKeyCode();
	if (k == KeyEvent.VK_SPACE) {
	    System.out.print("按下空格");
	}
	if (k == KeyEvent.VK_LEFT && A.NODES[myx - 1][myy] != 0 && myx - 1 >= 1) {
	    myx--;
	}
	if (k == KeyEvent.VK_RIGHT && A.NODES[myx + 1][myy] != 0 && myx + 1 <= 21) {
	    myx++;
	}
	if (k == KeyEvent.VK_UP && A.NODES[myx][myy - 1] != 0 && myy - 1 >= 1) {
	    myy--;
	}
	if (k == KeyEvent.VK_DOWN && A.NODES[myx][myy + 1] != 0 && myy + 1 <= 21) {
	    myy++;
	}
	repaint();
    }
    @Override
    public void keyReleased(KeyEvent e) {
    }
    @Override
    public void mousePressed(MouseEvent e) {
    }
    @Override
    public void mouseReleased(MouseEvent e) {
    }
    @Override
    public void mouseEntered(MouseEvent e) {
    }
    @Override
    public void mouseExited(MouseEvent e) {
    }
}

（3）Maze类

package Maez;
import java.util.Random; 

public class Maze {
    public static int row = 10;// 初始地图有路的迷宫单元行数
    public static int column = 10;// 初始地图有路的迷宫单元列数
    public static int r = 2 * row + 1;// 迷宫单元行数，保证是奇数
    public static int c = 2 * column + 1;// 迷宫单元列数，保证是奇数
    public static int[][] LabId;// 存放迷宫的数组,迷宫单元数组
    Random rand = new Random();

    public Maze() {
	LabId = new int[r][c];
	System.out.println("初始化地图:");
	for (int i = 0; i < r; i++) {
	    for (int j = 0; j < c; j++) {
		LabId[i][j] = 0;// 将所有格子都设为墙, 0 为墙 1为路
		if (i % 2 == 1 && j % 2 == 1)// 将奇数行奇数列设为路，1为路，0为墙
		    LabId[i][j] = 1;
		System.out.print(LabId[i][j] + " ");// 打印初始化地图，在控制台输出查看
	    } 
	    System.out.println();
	}

	// 调用深度优先搜索算法
	accLabDFS();
	System.out.println("\n" + "深度优先算法生成的迷宫:");
	for (int i = 0; i < r; i++) {
	    for (int j = 0; j < c; j++) {
		System.out.print(LabId[i][j] + " ");// 打印生成的深度优先算法生成的迷宫，在控制台输出查看
	    } 
	    System.out.println();
	}
    }

    // 实现深度优先算法
    public void accLabDFS() {
	int[] lab;// 访问队列
	int count = row * column;// 所有的迷宫单元数，不包括墙
	lab = new int[count];
	for (int i = 0; i < count; i++)
	    lab[i] = 0;// 设置所有单元都为未访问过的，0表示未访问过，1表示已访问过
	for (int v = 0; v < count; v++) {// 从第0个点开始遍历
	    if (lab[v] != 1) {// 如果该单元还未被访问，则递归调用深度优先算法遍历
		DFS(lab, v);
	    }
	}
    }


    // 使用DFS算法,借助递归思想访问某一顶点v,找v点附近且未被访问的点w,在找w附近未被访问的点(循环...),直到没有继续能找下去的点,
    // 依次退回最近被访问的点,如果还有该顶点的其他邻居没有被访问,就从邻居点开始继续搜索,把相邻的部分格子打通
    public void DFS(int[] LabG, int v) {
	LabG[v] = 1;// 访问顶点
	int[] neighbor = { v + row, v - row, v - 1, v + 1 };// 该点的四个邻居 上下左右
	int[] offR = { 0, 0, -1, 1 }, offC = { 1, -1, 0, 0 };// Row上个方向的偏移 Column上各方向的偏移，上下左右
	int[] tag = { -1, -1, -1, -1 };// 记录打通位置
	int n = 0;// 打通的次数
	while (n < 4) {// 上下左右四个方向都遍历，
	    int i = rand.nextInt(4);// 随机打通一个方向
	    if (tag[i] == 1)
		continue;// 进入下一轮循环
	    tag[i] = 1;// 打通墙，设为1
	    n++;
	    int w = neighbor[i];// 定义一个该方向上的邻居
	    if (w > LabG.length - 1 || w < 0)
		continue; // w不存在,即该方向上没有邻居

	    // 取出现在的v点的位置
	    int x = v % row;
	    int y = v / row;

	    // 遍历到四个边界时再往边界方向就没有邻居了，进入下一轮循环
	    if (i == 0 && y == column - 1)
		continue;// 上方向
	    if (i == 1 && y == 0)
		continue;// 下方向
	    if (i == 2 && x == 0)
		continue;// 左方向
	    if (i == 3 && x == row - 1)
		continue;// 右方向

	    // 如果该点有未访问的邻居，则把该点与其邻居间的墙打通，即相邻的格子中间的位置放1
	    if (LabG[w] == 0) {
		LabId[2 * x + 1 + offR[i]][2 * y + 1 + offC[i]] = 1;
		DFS(LabG, w);// 递归
	    }
	}
    }
}

（4）AStart类

package Maez;
import java.util.ArrayList;
import java.util.List;
 
public class AStart {  
    public static int[][] NODES;//定义一个迷宫单元数组
    public  int STEP = 10;//设每一步的权值为10
    private ArrayList<Node> openList = new ArrayList<Node>();//维护一个开放列表
    private ArrayList<Node> closeList = new ArrayList<Node>();//维护一个关闭列表
        
	public AStart() {
	NODES=Maze.LabId;//初始化迷宫单元为新生成的对应地图，把Maze2类里面生成的地图传给NODES，再在此地图基础上用A*算法寻路径
        Node startNode = new Node(1, 1);//起点
        Node endNode = new Node(19, 19);//终点
        Node parent = findPath(startNode, endNode); //父节点        
        ArrayList<Node> arrayList = new ArrayList<Node>(); 
        while (parent != null) {          
            arrayList.add(new Node(parent.x, parent.y));
            parent = parent.parent;
        }    
        
        //打印有路径的地图，在控制台输出查看
        System.out.println("\n"+"打印有路径的地图:");
        for (int i = 0; i < NODES.length; i++) {
            for (int j = 0; j < NODES.length; j++) {
                if (exists(arrayList, i, j)) {
                    NODES[i][j]=2;//标记关闭列表里的方格为2，为了方便后面在界面画系统寻路路径                 
                }  
		System.out.print(NODES[i][j] + " ");                
            }     
            System.out.println();
        }     
    }

    //寻找开放列表里F值最小的节点的方法
    public Node findMinFNodeInOpneList() {
        Node tempNode = openList.get(0);
        for (Node node : openList) {
            if (node.F < tempNode.F) {
                tempNode = node;
            }
        }
        return tempNode;
    }
    
    //遍历当前节点上下左右四个邻居的方法，
    public ArrayList<Node> findNeighborNodes(Node currentNode) {
        ArrayList<Node> arrayList = new ArrayList<Node>();
        // 只考虑上下左右，不考虑斜对角
        int topX = currentNode.x;
        int topY = currentNode.y - 1;
        if (canReach(topX, topY) && !exists(closeList, topX, topY)) {
            arrayList.add(new Node(topX, topY));
        }
        int bottomX = currentNode.x;
        int bottomY = currentNode.y + 1;
        if (canReach(bottomX, bottomY) && !exists(closeList, bottomX, bottomY)) {
            arrayList.add(new Node(bottomX, bottomY));
        }
        int leftX = currentNode.x - 1;
        int leftY = currentNode.y;
        if (canReach(leftX, leftY) && !exists(closeList, leftX, leftY)) {
            arrayList.add(new Node(leftX, leftY));
        }
        int rightX = currentNode.x + 1;
        int rightY = currentNode.y;
        if (canReach(rightX, rightY) && !exists(closeList, rightX, rightY)) {
            arrayList.add(new Node(rightX, rightY));
        }
        return arrayList;
    }
 
    
    //判断此处坐标是否可达，若超界或者是墙则不可达
    public boolean canReach(int x, int y) {
        if (x >=0 && x < NODES.length && y >=0 && y < NODES.length && NODES[x][y]==1) {
            return true;
        }
        return false;
    }
 
  
    //A*寻路过程
    public Node findPath(Node startNode, Node endNode) {       
        openList.add(startNode);// 把起点加入 open list
        while (openList.size() > 0) {         
            Node currentNode = findMinFNodeInOpneList();// 遍历 open list ，查找 F值最小的节点，把它作为当前要处理的节点   
            openList.remove(currentNode);// 从open list中移除          
            closeList.add(currentNode);// 把这个节点移到 close list
            ArrayList<Node> neighborNodes = findNeighborNodes(currentNode);
            for (Node node : neighborNodes) {//遍历四个邻居
                if (exists(openList, node)) {
                    foundPoint(currentNode, node);
                } else {
                    notFoundPoint(currentNode, endNode, node);
                }
            }          
            if (find(openList, endNode) != null) {       	
                return find(openList, endNode);//找到终点了并返回
            }
        }
        return find(openList, endNode);
    }
   
    //在列表里可以找到节点后的情况
    private void foundPoint(Node tempStart, Node node) {
        int G = calcG(tempStart, node);
        if (G < node.G) {
            node.parent = tempStart;
            node.G = G;
            node.calcF();
        }
    }
 
    //在节点里找不到节点的情况
    private void notFoundPoint(Node tempStart, Node end, Node node) {
        node.parent = tempStart;
        node.G = calcG(tempStart, node);
        node.H = calcH(end, node);
        node.calcF();
        openList.add(node);
    }
 
 
    //计算G值的方法
    private int calcG(Node start, Node node) {
        int G = STEP;
        int parentG = node.parent != null ? node.parent.G : 0;
        return G + parentG;
    }
    
    //计算H值的方法
    private int calcH(Node end, Node node) {
        int step = Math.abs(node.x - end.x) + Math.abs(node.y - end.y);
        return step * STEP;
    }
    
    //找到终点的方法
    public static Node find(List<Node> nodes, Node point) {
        for (Node n : nodes)
            if ((n.x == point.x) && (n.y == point.y)) {
                return n;
            }
        return null;
    }
 
    //下面两个是exist方法的重载，判断不同参数情况时节点是否在列表里
    public static boolean exists(List<Node> nodes, Node node) {
        for (Node n : nodes) {
            if ((n.x == node.x) && (n.y == node.y)) {
                return true;
            }
        }
        return false;
    }
 
    public static boolean exists(List<Node> nodes, int x, int y) {
        for (Node n : nodes) {
            if ((n.x == x) && (n.y == y)) {
                return true;
            }
        }
        return false;
    }
     
    //节点类，定义了每一个节点的属性
    public static class Node {
        public Node(int x, int y) {
            this.x = x;
            this.y = y;
        }
        public int x;
        public int y;
        public int F;
        public int G;
        public int H;
 
        public void calcF() {
            this.F = this.G + this.H;
        }      
        public Node parent;
    }
}

六、参考文献

1、深度优先算法生成迷宫

https://blog.csdn.net/qq_38064109/article/details/93554529

2、A*算法走迷宫

https://blog.csdn.net/qq_36946274/article/details/81982691