数据结构_进阶(2):二叉树的OJ练习题
目录
1. 二叉树创建字符串。OJ链接
2. 二叉树的分层遍历1。OJ链接
3. 二叉树的分层遍历2。OJ链接
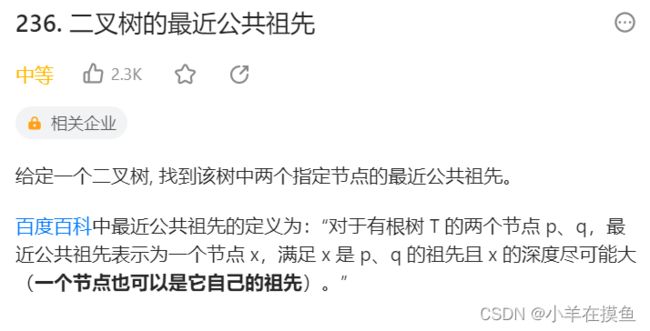
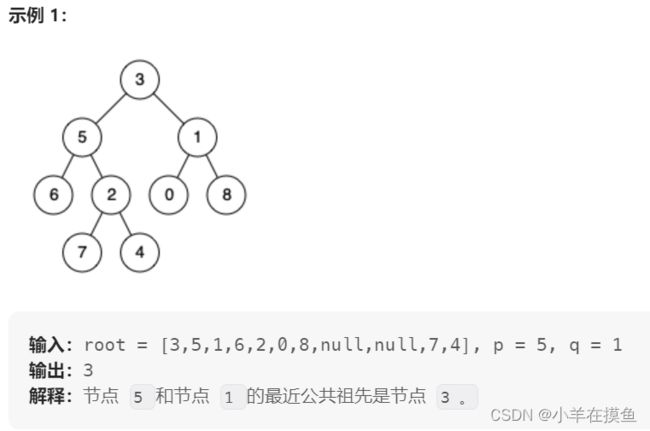
4. 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先 。OJ链接
5. 二叉树搜索树转换成排序双向链表。OJ链接
6. 根据一棵树的前序遍历与中序遍历构造二叉树。 OJ链接
7. 根据一棵树的中序遍历与后序遍历构造二叉树。OJ链接
8. 二叉树的前序遍历,非递归迭代实现 。OJ链接
9. 二叉树的中序遍历 ,非递归迭代实现。OJ链接
10. 二叉树的后序遍历 ,非递归迭代实现。OJ链接
1. 二叉树创建字符串。OJ链接
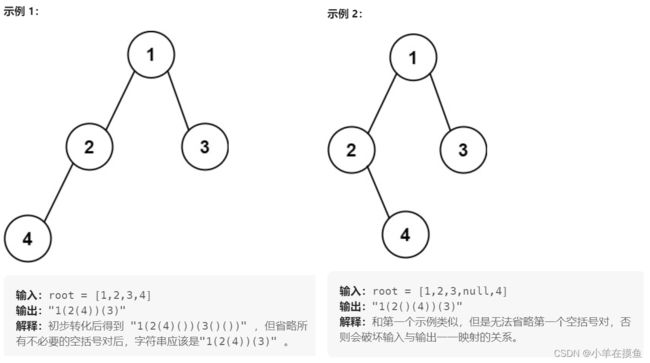
分析题型如下:
根据示例可以看到其省的括号并不是把所有的都省了,而是会保留左子树的括号
左右都为空省略,左为空不能省略,右为空可以省略
思路:
用递归遍历整棵树,注意要将每个节点的值转为字符串类型,再利用重载的+=来添加括号
我们先写一个不省略括号的代码,然后根据之前的三个条件进行限制
不省略括号的代码如下:
根据条件加入限制得到:
class Solution {
public:
string tree2str(TreeNode* root) {
if(root == nullptr)
return "";
string str = to_string(root->val);
// 先判断左是否为空,不为空:继续;为空:再判断右为不为空;
// 不为空:左不能省,继续;
// 为空,那么此时左右都为空,就可以省略了。
if(root->left || root->right)
{
str += '(';
str += tree2str(root->left);
str += ')';
}
// 在上面条件判断后,再判断右是否为空
// 如果右为空:省略;右不为空:继续。
if(root->right)
{
str += '(';
str += tree2str(root->right);
str += ')';
}
return str;
}
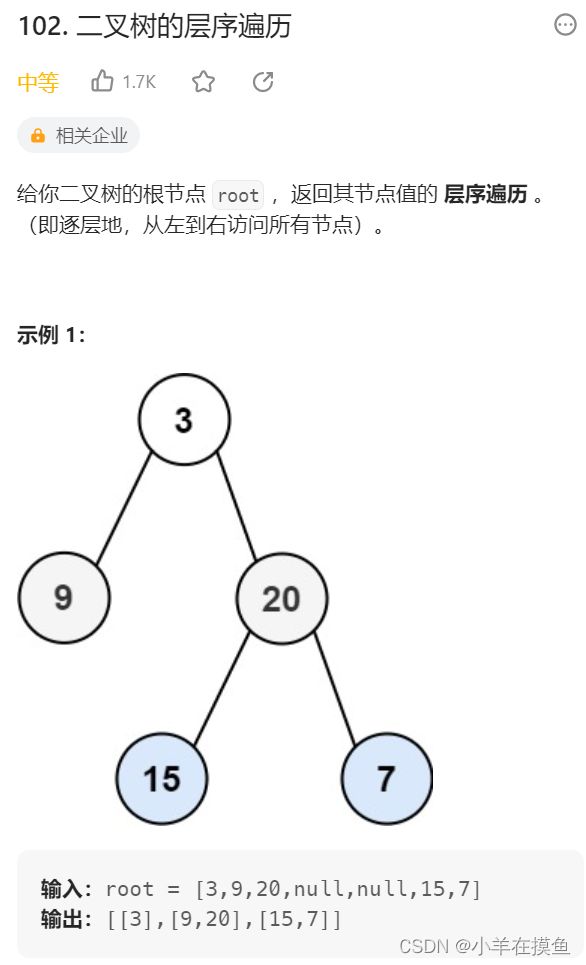
};2. 二叉树的分层遍历1。OJ链接
思路:
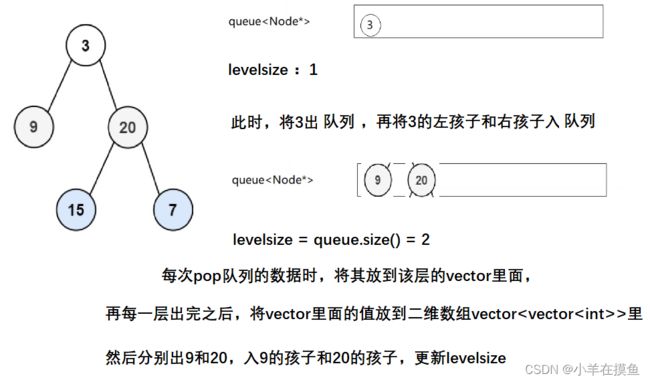
用一个队列来存放数据,在这个队列出数据的时候,将其的左右节点入栈,
再定义一个变量 levelsize 用来存储该层有多少个数
具体如下图:
代码:
class Solution {
public:
// vector>二维数组
vector> levelOrder(TreeNode* root) {
queue q;
int levelsize = 0;
if(root)
{
q.push(root);
levelsize = 1;
}
vector> vv;
//当队列为空时结束
while(!q.empty())
{
// 通过levelsize来控制一层一层的出
vector v;//把每一层的数据放到一个vector里面
while(levelsize--)
{
TreeNode* F = q.front();//F就是此时要控制的树的节点
q.pop();
v.push_back(F->val);
if(F->left)
q.push(F->left);
if(F->right)
q.push(F->right);
}
// 将第每一层的数组v放到二维数组中
vv.push_back(v);
// 更新下一层的数据
levelsize = q.size();
}
return vv;
}
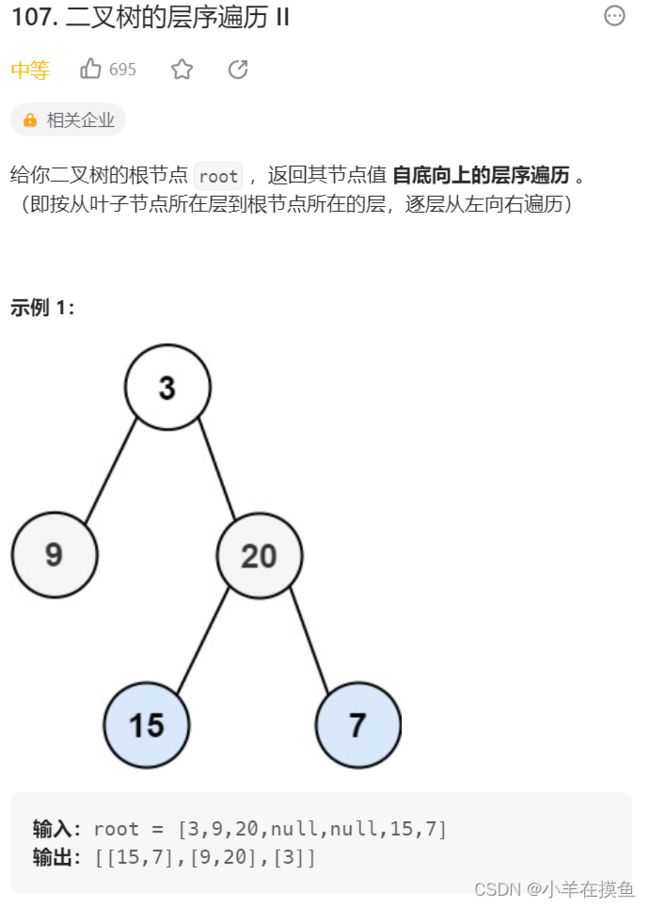
}; 3. 二叉树的分层遍历2。OJ链接
思路:
这道题的思路和上面那道题的思路一模一样,只是我们在最后需要稍微处理一下,使其反转打印
我们C++里面的算法头文件里面有一个reverse的逆置算法
正好可以用到此问题上
class Solution {
public:
vector> levelOrderBottom(TreeNode* root) {
queue q;
int levelsize = 0;
if(root)
{
q.push(root);
levelsize = 1;
}
vector> vv;
//当队列为空时结束
while(!q.empty())
{
// 通过levelsize来控制一层一层的出
vector v;//把每一层的数据放到一个vector里面
while(levelsize--)
{
TreeNode* F = q.front();//F就是此时要控制的树的节点
q.pop();
v.push_back(F->val);
if(F->left)
q.push(F->left);
if(F->right)
q.push(F->right);
}
// 将第每一层的数组v放到二维数组中
vv.push_back(v);
// 更新下一层的数据
levelsize = q.size();
}
// 反转
reverse(vv.begin(), vv.end());
return vv;
}
}; 4. 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先 。OJ链接
思路1:
首先我们要找最近的公共祖先,那么孩子肯定是在这个公共祖先的一左一右
p、q 是题目给我们的两个数,我们先找这两个数是在,此时节点的左边还是右边
此时会有三种情况:
1)如果p再左,q再右;或者,q在左,p在右。那么此时节点就是最近公共祖先
2)如果都在左,转换为子问题,递归到左子树去找公共祖先
3)如果都在右,转换为子问题,递归到右子树去找公共祖先
class Solution {
public:
//写判断p、q在左还是右的函数
bool IsInTree(TreeNode* root, TreeNode* x)
{
if(root == nullptr)
{
return false;
}
if(root == x)
return true;
else
return IsInTree(root->left, x) || IsInTree(root->right, x);
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
//跟为空返回空
if(root == nullptr)
return nullptr;
//如果p或q有一个为跟,另一个是孩子,root就是最近祖先
if(p == root || q == root)
return root;
//判断p、q在左边还是右边
bool pInLift = IsInTree(root->left, p);
bool pInRight = !pInLift;
bool qInLift = IsInTree(root->left, q);
bool qInRight = !qInLift;
//1.如果一个在左,一个在右。那么此时节点就是最近公共祖先
//2.如果都在左,转换为子问题,递归到左子树去找公共祖先
//3.如果都在右,转换为子问题,递归到右子树去找公共祖先
if((pInLift && qInRight) || (qInLift && pInRight))
{
return root;
}
else if(pInLift && qInLift)
{
return lowestCommonAncestor(root->left, p, q);
}
else
{
return lowestCommonAncestor(root->right, p, q);
}
}
};思路2:
我们可以看到按照思路1来写的代码可以通过,但比较费时间
我们可以来算一下思路1代码的时间复杂度:
可能会有人觉得上述代码的时间复杂度是 O(n*logN),查找是N,高度是logN
但实际上并不是,我们要注意:只有完全二叉树和满二叉树我们才能认为它的高度是 logN
因为有可能是课歪脖子树,所以上述代码的时间复杂度是 O(n^2)
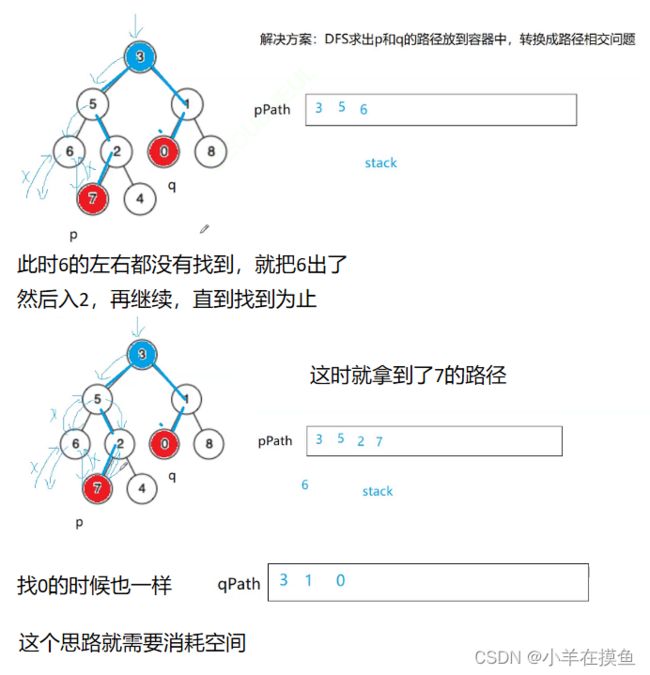
思路二就是用两个栈来记录p、q的路径,然后将两个路径进行比较
从3的左边开始遍历到6的时候左右都没有,就把6出了
class Solution {
public:
bool Getpath(TreeNode* root, TreeNode*x, stack& path)
{
//先写递归结束条件
if(root == nullptr)
return false;
//入栈
path.push(root);
// 等于要找的数,结束
if(root == x)
return true;
// 不等于,继续递归找
if(Getpath(root->left, x, path))
return true;
if(Getpath(root->right, x, path))
return true;
//递归到头都没找到,则出栈
path.pop();
return false;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q)
{
// 定义两个栈,一个存放p的路径,一个存放q的路径
stack pPath, qPath;
// 找p和q,并记录其路径
Getpath(root, p, pPath);
Getpath(root, q, qPath);
// 将长路径出,直到到和短路径一样长
while(pPath.size() != qPath.size())
{
if(pPath.size() > qPath.size())
pPath.pop();
else
qPath.pop();
}
// 两个一起出,直到他们有相等的值结束
while(pPath.top() != qPath.top())
{
pPath.pop();
qPath.pop();
}
//此时不管是pPath还是qPath的首元素都是最进祖先
return qPath.top();
}
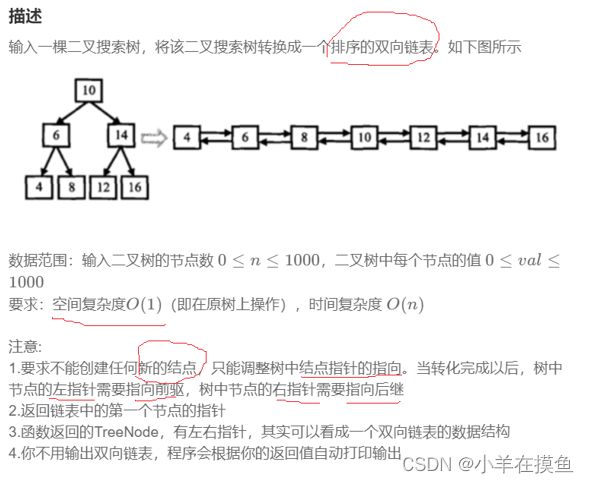
}; 5. 二叉树搜索树转换成排序双向链表。OJ链接
要求里面需要我们在原树上进行修改,并且空间复杂读为 O(1),
如果没有这个要求,我们就可以将其中序遍历存放到vector中,然后再该链接关系,就会非常简单
思路:
我们还是中序遍历该树,得到:4,6,8,10,12,14,16
同时记录一个前驱prev,一个当前cur;因为是中序遍历,所以一个数的左一定是指向前驱的
此时难点在于找后继节点:我们让cur->left = prev ,让prev->right = cur
最后,在修改完之后我们只能拿到root跟节点,但这个根节点不是循环链表的头,所以我们只需要去往左走,走到头即可
class Solution
{
public:
// prev在递归是不能改变,所以需要引用起别名
void InorderTraversal(TreeNode* cur, TreeNode*& prev)
{
if(cur == nullptr)
return;
//中序遍历
InorderTraversal(cur->left, prev);
cur->left = prev;
//防止刚开始prev为空
if(prev)
prev->right = cur;
prev = cur;
InorderTraversal(cur->right, prev);
}
TreeNode* Convert(TreeNode* pRootOfTree)
{
TreeNode* prev = nullptr;
InorderTraversal(pRootOfTree, prev);
TreeNode* head = pRootOfTree;
// 寻找头结点
while(head && head->left)
head = head->left;
return head;
}
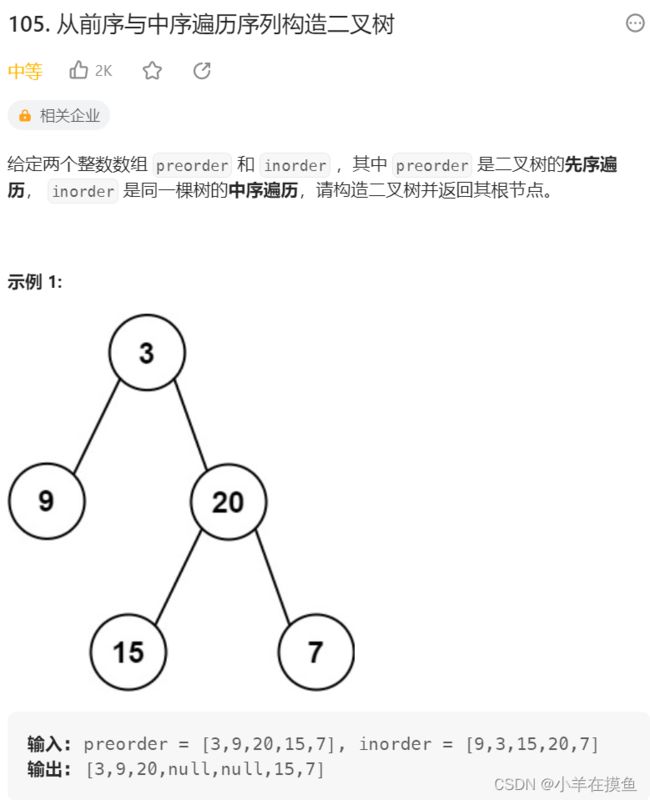
};6. 根据一棵树的前序遍历与中序遍历构造二叉树。 OJ链接
思路:
通过前序数组不断去确定根,然后对中序数组进行空间划分,当空间没有是返回根
class Solution
{
public:
// 因为需要递归,不好再原树上进行操作,所以先建立一个子函数
// int& prei定义前序的一个下标需要一直往后走,中序需要定义一段区间,来分割子树:inbegin、inend
TreeNode* _buildTree(vector& preorder, vector& inorder, int& prei, int inbegin, int inend)
{
// 结束条件
if(inbegin > inend)
return nullptr;
TreeNode* root = new TreeNode(preorder[prei]);
// 分割出左右区间
int rooti = inbegin;
// 再中序数组里面找到根
while(rooti <= inend)
{
//判断中序数组里的值与前序数组里的值是否相等,相等找到,不相等继续找
if(inorder[rooti] == preorder[prei])
break;
else
rooti++;
}
// 此时在前序数组里面找下一个左子树的根节点
++prei;
// 中序数组被分割出了三段区间:[inbegin, rooti-1]; rooti; [rooti+1,inend]
root->left = _buildTree(preorder, inorder, prei, inbegin, rooti-1);
root->right = _buildTree(preorder, inorder, prei, rooti+1, inend);
return root;
}
TreeNode* buildTree(vector& preorder, vector& inorder)
{
int i = 0;
return _buildTree(preorder, inorder, i, 0, inorder.size()-1);
}
}; 7. 根据一棵树的中序遍历与后序遍历构造二叉树。OJ链接
和上一题的解题思路一致,只是把从前序数组的前往后找根节点,换位了,后序数组的从后往前找根节点,需要注意的是,在建立二叉树的过程中,需要先构建右子树,然后再构建左子树
class Solution {
public:
TreeNode* _buildTree(vector& postorder, vector& inorder, int& prei, int inbegin, int inend)
{
// 结束条件
if(inend < inbegin)
return nullptr;
TreeNode* root = new TreeNode(postorder[prei]);
// 分割出左右区间
int rooti = inbegin;
// 再中序数组里面找到根
while(rooti <= inend) //rooti <= inend
{
//判断中序数组里的值与后序数组里的值是否相等,相等找到,不相等继续找
if(inorder[rooti] == postorder[prei])
break;
else
rooti++;
}
// 此时在后序数组里面找下一个左子树的根节点
--prei;
// 中序数组被分割出了三段区间:[inbegin, rooti-1]; rooti; [rooti+1,inend]
root->right = _buildTree(postorder, inorder, prei, rooti+1, inend);
root->left = _buildTree(postorder, inorder, prei, inbegin, rooti-1);
return root;
}
TreeNode* buildTree(vector& inorder, vector& postorder)
{
int i = postorder.size()-1;
return _buildTree(postorder, inorder, i, 0, inorder.size()-1);
}
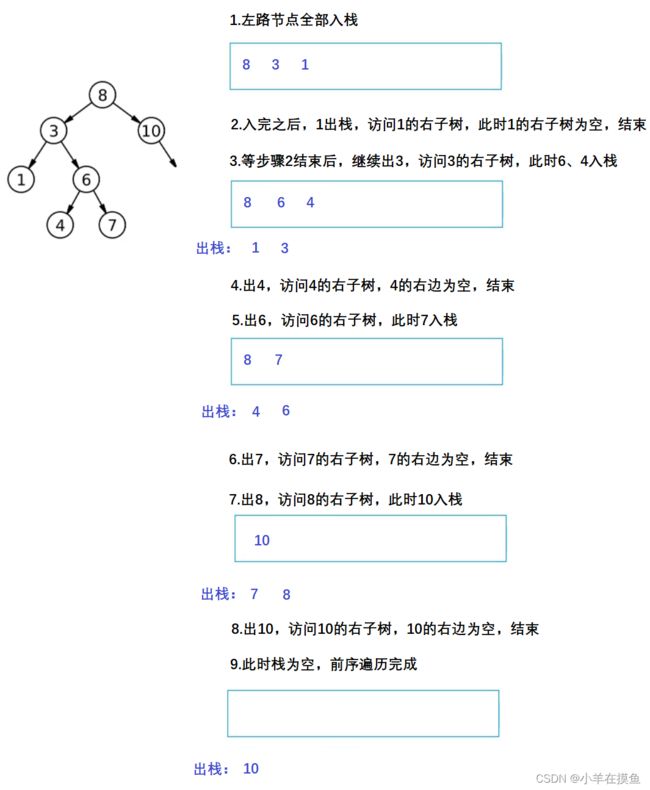
}; 8. 二叉树的前序遍历,非递归迭代实现 。OJ链接
思路:
还是用栈,先把左路的数都放入栈,然后再依次出栈,其孩子入栈
- 1.左路节点
- 2.左路节点的右子树
这里的右子树怎么访问?
继续变为子问题,再继续左路节点,如下图详解:
下图中入栈顺序是前序的顺序,出栈顺序是后续的顺序
代码如下:
class Solution {
public:
// 非递归实现:
vector preorderTraversal(TreeNode* root)
{
// 创建一个栈来存放数据
stack st;
TreeNode* cur = root;
// 创建对象v来存放出栈的数据
vector v;
// 需要cur为空并且栈为空才会结束
while(cur || !st.empty())
{
// 一直往左边去走,直到左边为空
while(cur)
{
// 入栈前,给数组v尾插数据
v.push_back(cur->val);
// 将左树的值入栈
st.push(cur);
//继续往左走
cur = cur->left;
}
//左为空后出栈,走右
//取栈顶数据,然后出栈
TreeNode* top = st.top();
st.pop();
cur = top->right;
}
return v;
}
}; 9. 二叉树的中序遍历 ,非递归迭代实现。OJ链接
思路:
和前序队列一样,仔细观察前序队列的图,就可以发现,每次出栈的顺序就是中序队列的顺序,所以下面代码仅仅只是将vector的尾插放在了出栈前而不是入栈前。
class Solution {
public:
vector inorderTraversal(TreeNode* root) {
// 创建一个栈来存放数据
stack st;
TreeNode* cur = root;
// 创建对象v来存放出栈的数据
vector v;
// 需要cur为空并且栈为空才会结束
while(cur || !st.empty())
{
// 一直往左边去走,直到左边为空
while(cur)
{
// 将左树的值入栈
st.push(cur);
//继续往左走
cur = cur->left;
}
//左为空后出栈,走右
//取栈顶数据,然后出栈
TreeNode* top = st.top();
//出栈时,给v里面放入数据,此时将会是中序队列
v.push_back(top->val);
st.pop();
cur = top->right;
}
return v;
}
}; 10. 二叉树的后序遍历 ,非递归迭代实现。OJ链接
后序遍历比前序和中序要难思考一点,所以一般笔试什么的都会考后序遍历
思路1:
我们先走左子树,走到最后一个左子树的时候
1)当其右子树为空,我们可以直接拿取
2)当右子树不为空,我们第二次走到父节点时,拿取(举个例子,如下:)

我们会在第二次访问的时候拿取
代码如下:(注意看注释理解)
class Solution {
public:
vector postorderTraversal(TreeNode* root) {
// 创建一个栈来存放数据
stack st;
TreeNode* cur = root;
// 创建对象v来存放出栈的数据
vector v;
// 加入
TreeNode* prev = nullptr;
// 需要cur为空并且栈为空才会结束
while(cur || !st.empty())
{
// 一直往左边去走,直到左边为空
while(cur)
{
// 将左树的值入栈
st.push(cur);
//继续往左走
cur = cur->left;
}
//左为空后出栈,走右
//取栈顶数据,然后出栈
TreeNode* top = st.top();
//1、右为空,可以访问跟节点
//2、右子树已经被访问过了(上一个访问的节点是右子树的根)
if(top->right == nullptr || top->right == prev)
{
v.push_back(top->val);
st.pop();
prev = top;
}
else
{
//访问右子树,子问题
cur = top->right;
}
}
return v;
}
}; 思路2:
后序遍历的访问方式是:左右根,我们把它逆置一下变为:根右左,
和前序比较可以发现只需要改一下前序代码,
使其先入栈右边的树,然后再入左边的树,最后来个逆置也是可以的!
这种方法也是最简单的,也这算是一个取巧的操作,代码如下:
class Solution {
public:
// 非递归实现:
vector preorderTraversal(TreeNode* root)
{
// 创建一个栈来存放数据
stack st;
TreeNode* cur = root;
// 创建对象v来存放出栈的数据
vector v;
// 需要cur为空并且栈为空才会结束
while(cur || !st.empty())
{
// 一直往右边去走,直到右边为空
while(cur)
{
// 入栈前,给数组v尾插数据
v.push_back(cur->val);
// 将左树的值入栈
st.push(cur);
//继续往右走
cur = cur->right;
}
//左为空后出栈,走右
//取栈顶数据,然后出栈
TreeNode* top = st.top();
st.pop();
cur = top->left;
}
reverse(v.begin(), v.end());
return v;
}
};