PSO算法介绍

一、背景知识

        1.创立者信息

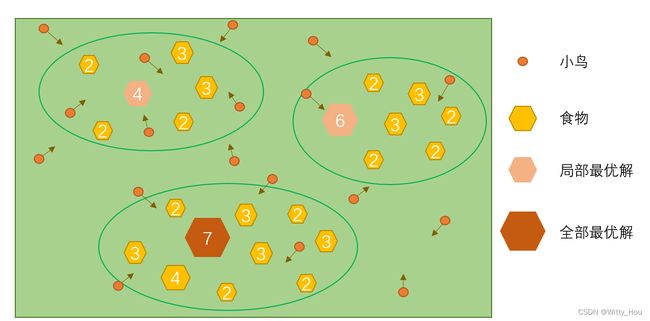
       粒子群算法是美国学者Kennedy和Eberhart共同提出的，其核心思想源于鸟群觅食行为规律，利用群体中的个体对信息的共享，使整个群体在探索空间时可以分工完成对各个区域的检索，最终找到有食物的位置。

         2.基本思想

       鸟群在一块新的地区觅食，在开始阶段，每只小鸟都沿着自己认为可能存在食物的地方前进，并在搜索过程中记下自己看到的食物最多的地方。鸟群汇合的时候共享一下自己发现的信息，就能知道目前食物最多的地方，每只小鸟再根据自己搜索到的信息和团队共享的信息重新搜索，经过几次共享后，鸟群就可以找到食物最多的地方。

觅食示意图

 

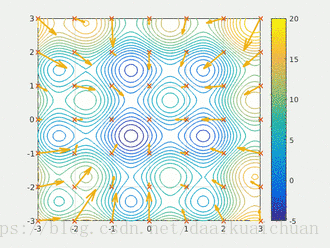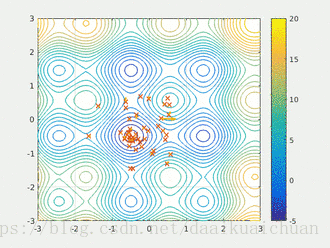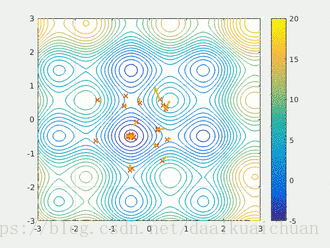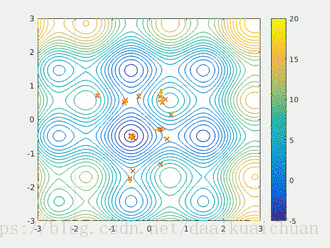
粒子群算法作用过程

        3.特点及缺陷

       PSO具有收敛速度快、参数少、算法简单易于实现等优点，但PSO由于存在迭代次数、判断公式的限制、群体粒子数量、求解参数的个数、求解问题是单峰还是多峰等诸多因素，PSO不可避免地会遇到陷入局部最优解问题。

二、PSO算法基本原理

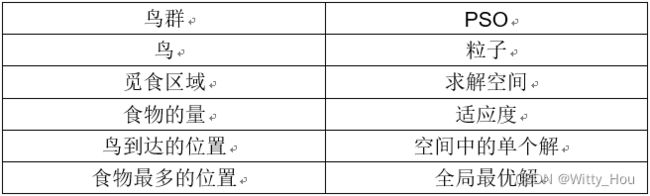
鸟群觅食与PSO的对应关系

        1.PSO实现基础：信息共享

粒子群中每一轮迭代，所有粒子对目前所在的位置（解）进行一次适应度判断，与自己到过的最优点、当前群体最优点进行比较，如果更好就替代个体/群体最优值。每一轮迭代结束后，将当前的群体最优与之前记录的群体最优值进行比较，适应度更好则更新群体最优记录。当适应度满足要求或迭代完成之后，就可以输出最终的迭代结果。

        2.PSO算法中会用到的参数及其含义

 

       3.粒子的两个重要属性：速度和位置

       位置部分：

PSO算法的核心是通过粒子在求解空间内多次有规律地移动来验证各个点位的适应度，因此粒子在运行时，需要不断更新自己的位置，来探索更多的点。因此PSO的粒子就有对应的位置更新公式：

       上述公式内包含三项：三项、 、

       PSO是一个迭代算法，因此会有存在前后两代之间的联系，k+1代的位置是在第k代的位置基础上加上第k+1代的位移（vk+1）。因此该参数虽然用v来表示，且称之为速度，但从本质上来讲，它是一段在空间内的位移。

       速度（位移）部分：

       PSO是通过粒子在空间内不断搜索坐标点来验证，而如何确定粒子接下来的位移是PSO的重点。PSO算法中，位移与三部分有关：本身上次的位移、个体到达的最佳位置、群体最佳位置，通过三者加权来确定下一次的位移。

       公式内包含了三部分：

       （1）惯性部分

       由惯性权重和粒子自身位移构成，表示粒子对自己本身当前运动状态的依赖程度。

       （2）认知部分

       由学习因子、随机数和当前位置与自己曾经达到的最优位置的位置差，表示粒子对自身的思考，对自己探索结果的信赖程度。

       （3）社会部分

由学习因子、随机数和当前位置与群体曾经到达的最优位置的位置差，表示粒子对群体结果的思考，对群体探索结果的信赖程度。

        示意图：

        4.粒子群算法流程图

        5.粒子群算法的演算示例

       求解问题：，其中

三、PSO算法参数的设计 1.粒子群规模N

      1.粒子群规模N

        一个正整数，推荐取值范围：[20,1000]，简单问题一般取20~40，较难或特定类别的问题可以取100~200。较小的种群规模容易陷入局部最优；较大的种群规模可以提高收敛性，更快找到全局最优解，但是相应地每次迭代的计算量也会增大；当种群规模增大至一定水平时，再增大将不再有显著的作用。

        2.粒子维度D

       自变量的个数。

       3.迭代次数K

       推荐取值范围：[50,100]，典型取值：60、70、100；在实际使用时，需要和N配合，在取值合适能求得期望解时就足够。过大的迭代次数会浪费计算量，过小则会导致没办法求得最优解。

       4.惯性权重ω

       ω表示上一代粒子对当代粒子的位移影响，表示了粒子对自身运动状态的信任程度。惯性权重越大，粒子探索新区域的能力越强，全局寻优能力越强，但相应的局部寻优能力会减弱。因此较大的​​​​​​​ω利于全局寻优，跳出局部极值；而较小的​​​​​​​ω有利于局部搜索，让算法收敛到最优解。但是当空间较大的时候，为了平衡求解速度和探索精度，通常是采用变化的​​​​​​​ω，在初期使用较大的​​​​​​​ω值，强化全局探索能力，在后期采用较小的​​​​​​​ω值，提高收敛精度。

       通常​​​​​​​ω取值范围为[0.4,2]，典型取值：0.9、1.2、1.5、1.8

       在解决实际问题时，通常希望先采用全局搜索，使搜索空间快速收敛于某一个区域，然后采用局部精细搜索以获得高精度的解。因此提出了自适应调整的策略，使ω随着迭代次数的增加，不断调整，通常采用的是线性变化策略。使得PSO在初期有较强的全局探索能力，在后期有较强的局部收敛能力。

        5.学习因子c1、c2

        c1表示粒子下一段位移源于自身经验的权重，即将粒子推向个体最优位置的权重。

        ​​​​​​​c2表示粒子下一段位移源于群体经验的权重，即将粒子推向群体最优位置的权重。

        当​​​​​​​c1=0时，变为无私型PSO，粒子容易陷入局部最优解。

        当c2=0时，变为认知型PSO，粒子全凭自身探索，收敛速度要慢很多。

        因此在正常的PSO中，​​​​​​​c1、c2均不为零，且部分算法中会采用变化的​​​​​​​c1、c2来强化PSO的寻优能力。一般来说c的取值范围为[0,4],典型固定值组合为：

       有文章提出可以使用变参数的c值来提升PSO的寻优能力，c的关系式为：

       6.适应度的设计

       适应度是用来判断粒子当前位置的好坏程度，决定是否更新群体和个体的最优位置和最优适应度，确保粒子朝着最优解的方向探索。合理的适应度设计是PSO能否收敛到最优解的关键，需要将自变量的好坏判断标准变为一个数学式，让其趋向于一个点，来确保PSO的收敛。

       7.位置和位移的限制

       粒子在解空间移动过程中，每次迭代都有一个实际的坐标点和一段位移向量，在迭代过程中，需要确保粒子移动始终在规定的解空间内，因此需要对粒子的位置进行限制。而位移限制的原因是，避免粒子单次漂移过大，增强粒子对局部空间的探索能力。

       8.跳出条件

       PSO程序何时结束目前有两种方法：

        设计最大迭代次数：

        设置PSO迭代次数，当程序运行完指定迭代次数后，输出最后得出的最优值，但是该方法最后输出的结果不一定是真实符合要求的解，因为PSO可能会陷入局部最优解。

       可接受的满意解：

       对适应度设置限制，当其与前几次的迭代值相差小于某一个值的时候就认为PSO已经收敛至一个最优解。

       将当前解带入数学式与实际实验值进行比对，如果与实验值的误差在可接受范围就认为PSO估算的参数与实际参数相吻合。

四、PSO算法实现

       PSO算法可以使用多种语言实现，本文以Python作为示例：

       1.定义一个粒子群

       首先需要定义一个粒子群，规定好其粒子数量、迭代次数、自变量个数、自变量的约束范围、位移约束范围、赋予每个粒子位置和位移变量并对变量进行归零操作。

def __init__(self, dimension, time, size, low, up, v_low, v_high):
       # 初始化
       self.dimension = dimension  # 变量个数
       self.time = time  # 迭代总代数
       self.size = size  # 种群大小
       self.bound = []  # 变量的约束范围
       self.bound.append(low)
       self.bound.append(up)
       self.v_low = v_low
       self.v_high = v_high
       self.x = np.zeros((self.size, self.dimension))  # 所有粒子的位置
       self.v = np.zeros((self.size, self.dimension))  # 所有粒子的速度
       self.p_best = np.zeros((self.size, self.dimension))  # 每个粒子最优的位置
       self.g_best = np.zeros((1, self.dimension))[0]  # 全局最优的位置

       2.对粒子群进行初始化

       设置粒子群的相关参数，给各个参数赋值，参数值会极大地影响PSO的收敛结果。参数设置完毕后，将粒子群中粒子进行一个初始化赋值，给它们一个初始的位置以及一段随机的位移，并将当前最优位置设置为初始位置。

# 初始化第0代初始全局最优解  
        for i in range(self.size):
            for j in range(self.dimension):
                self.x[i][j] = random.uniform(self.bound[0][j], self.bound[1][j])
                self.v[i][j] = random.uniform(self.v_low, self.v_high)
            self.p_best[i] = self.x[i]  # 储存最优的个体

       3.设计适应度函数

       适应度函数设计取决于绝对问题的形式，本示例是求解函数式在指定区间内的最大值，因此适应度函数就是求解函数本身。针对实际问题，则需要将遇到的问题转换为合适的数学表达式。

def fitness(self, x):
        """
        个体适应值计算：y = (sin(x1))^2 - cos(x2)
        """
        x1 = x[0]
        x2 = x[1]
        y =(np.sin(x1))**2 -(np.cos(x2))
        return y

       4.循环计算位置和位移公式

       在迭代次数内循环更新粒子群内各个粒子的位置，首先需要在粒子群内依次对每个粒子进行位置的更新，执行完一次整个粒子群的位置更新，才能进行下一次迭代。因此，粒子群算法的基础实现是双循环嵌套。

       如果未知数个数大于1，且各未知数的变化率不统一，需要三重嵌套来求解，对每个参数都单独设计一个位置位移，更新完一个粒子的所有参数，再完成上述的迭代过程。多重嵌套可能会提升收敛精度，但要求更高的算力。大家可以根据实际需要来设计是否加入第三层嵌套，参数保持同样的变化率也可以有很好的收敛效果。

       粒子的参数更新完毕后，带入适应度函数对粒子当前位置进行一个好坏判断，更新个体最优位置、个体最优适应度、群体最优位置和群体最优适应度。

#单次更新粒子群内各粒子的位置
def update(self, size, c1, c2, w):
        for i in range(size):
            # 更新速度(核心公式)
            self.v[i] = w * self.v[i] + c1 * random.uniform(0, 1) * (
                    self.p_best[i] - self.x[i]) + c2 * random.uniform(0, 1) * (self.g_best - self.x[i])
            # 速度限制
            for j in range(self.dimension):
                if self.v[i][j] < self.v_low:
                    self.v[i][j] = self.v_low
                if self.v[i][j] > self.v_high:
                    self.v[i][j] = self.v_high
            # 更新位置
            self.x[i] = self.x[i] + self.v[i]
            # 位置限制
            for j in range(self.dimension):
                if self.x[i][j] < self.bound[0][j]:
                    self.x[i][j] = self.bound[0][j]
                if self.x[i][j] > self.bound[1][j]:
                    self.x[i][j] = self.bound[1][j]
            # 更新p_best和g_best
            if self.fitness(self.x[i]) > self.fitness(self.p_best[i]):
                self.p_best[i] = self.x[i]
            if self.fitness(self.x[i]) > self.fitness(self.g_best):
                self.g_best = self.x[i]

#循环更新粒子群
for gen in range(self.time):
            c1 = 1.5 + np.sin(math.pi/2*(1-(2*gen/self.time))) # 学习因子
            c2 = 1.5 + np.sin(math.pi/2*((2*gen/self.time)-1))
            w = 1.6- 1.2*gen/self.time# 自身权重因子
            self.update(self.size, c1 ,c2, w)
            if self.fitness(self.g_best) > self.fitness(self.final_best):
                self.final_best = self.g_best.copy()
            print('当前最佳位置：{}'.format(self.final_best))
            temp = self.fitness(self.final_best)
            print('当前的最佳适应度：{}'.format(temp))
            best.append(temp)
            X1.append(self.final_best[0])
            X2.append(self.final_best[1])

       5.输出合适的结果

       结果输出可以是直接输出最终的求解结果，也可以设计一个图标，显示各参数的变化过程，取决于实际需求。

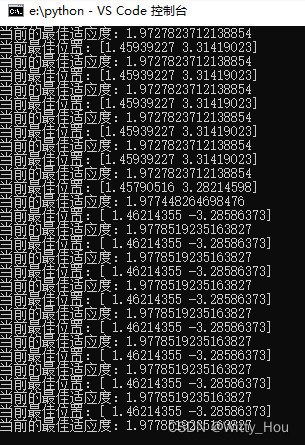
循环输出当代最优值：

 输出参数变化

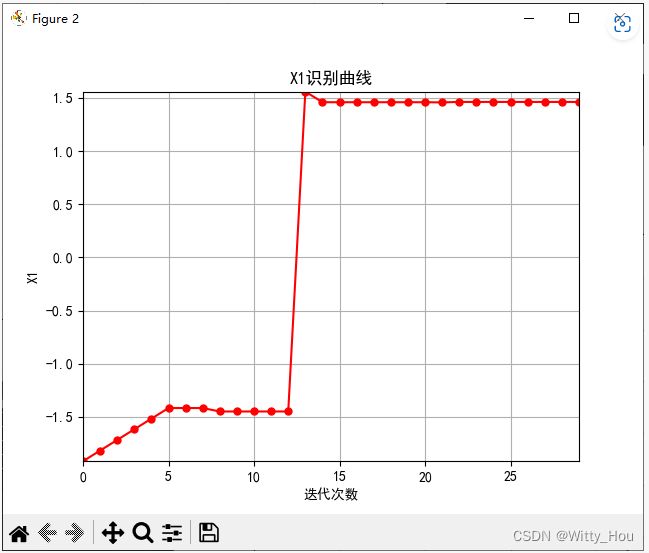
输出参数变化过程：

         6.完整算法

# -*- coding: utf-8 -*-
"""
@Time ： 2023/3/31 
@Author ：Witty
@File ：pso.py
"""
import math
import random
import numpy as np
import matplotlib.pyplot as plt
import pylab as mpl
mpl.rcParams['font.sans-serif'] = ['SimHei']


class PSO:
    def __init__(self, dimension, time, size, low, up, v_low, v_high):
        # 初始化
        self.dimension = dimension  # 变量个数
        self.time = time  # 迭代总代数
        self.size = size  # 种群大小
        self.bound = []  # 变量的约束范围
        self.bound.append(low)
        self.bound.append(up)
        self.v_low = v_low
        self.v_high = v_high
        self.x = np.zeros((self.size, self.dimension))  # 所有粒子的位置
        self.v = np.zeros((self.size, self.dimension))  # 所有粒子的速度
        self.p_best = np.zeros((self.size, self.dimension))  # 每个粒子最优的位置
        self.g_best = np.zeros((1, self.dimension))[0]  # 全局最优的位置


        # 初始化第0代初始全局最优解
        
        for i in range(self.size):
            for j in range(self.dimension):
                self.x[i][j] = random.uniform(self.bound[0][j], self.bound[1][j])
                self.v[i][j] = random.uniform(self.v_low, self.v_high)
            self.p_best[i] = self.x[i]  # 储存最优的个体
          
               
    def fitness(self, x):
        """
        个体适应值计算
        """
        x1 = x[0]
        x2 = x[1]
        y =(np.sin(x1))**2 -(np.cos(x2))
        return y

    def update(self, size, c1, c2, w):
        for i in range(size):
            # 更新速度(核心公式)
            self.v[i] = w * self.v[i] + c1 * random.uniform(0, 1) * (
                    self.p_best[i] - self.x[i]) + c2 * random.uniform(0, 1) * (self.g_best - self.x[i])
            # 速度限制
            for j in range(self.dimension):
                if self.v[i][j] < self.v_low:
                    self.v[i][j] = self.v_low
                if self.v[i][j] > self.v_high:
                    self.v[i][j] = self.v_high
            # 更新位置
            self.x[i] = self.x[i] + self.v[i]
            # 位置限制
            for j in range(self.dimension):
                if self.x[i][j] < self.bound[0][j]:
                    self.x[i][j] = self.bound[0][j]
                if self.x[i][j] > self.bound[1][j]:
                    self.x[i][j] = self.bound[1][j]
            # 更新p_best和g_best
            if self.fitness(self.x[i]) > self.fitness(self.p_best[i]):
                self.p_best[i] = self.x[i]
            if self.fitness(self.x[i]) > self.fitness(self.g_best):
                self.g_best = self.x[i]
    def pso(self):
        best = []
        X1 = []
        X2 = []

        self.final_best = np.array([1, 2])
        for gen in range(self.time):
            c1 = 1.5 + np.sin(math.pi/2*(1-(2*gen/self.time))) # 学习因子
            c2 = 1.5 + np.sin(math.pi/2*((2*gen/self.time)-1))
            w = 1.6- 1.2*gen/self.time# 自身权重因子
            self.update(self.size, c1 ,c2, w)
            if self.fitness(self.g_best) > self.fitness(self.final_best):
                self.final_best = self.g_best.copy()
            print('当前最佳位置：{}'.format(self.final_best))
            temp = self.fitness(self.final_best)
            print('当前的最佳适应度：{}'.format(temp))
            best.append(temp)
            X1.append(self.final_best[0])
            X2.append(self.final_best[1])
        
        t = [i for i in range(self.time)]
        plt.figure()
        plt.grid(ls='--')
        plt.plot(t, best, color='red', marker='.', ms=10)
        plt.rcParams['axes.unicode_minus'] = False
        plt.margins(0)
        plt.xlabel(u"迭代次数")  # X轴标签
        plt.ylabel(u"最大值")  # Y轴标签
        plt.title(u"迭代过程")  # 标题

        plt.figure()
        plt.grid(axis='both')
        plt.plot(t, X1, color='red', marker='.', ms=10)
        plt.rcParams['axes.unicode_minus'] = False
        plt.margins(0)
        plt.xlabel(u"迭代次数")  # X轴标签
        plt.ylabel(u"X1")  # Y轴标签
        plt.title(u"X1识别曲线")  # 标题

        plt.figure()
        plt.grid(axis='both')
        plt.plot(t, X2, color='red', marker='.', ms=10)
        plt.rcParams['axes.unicode_minus'] = False
        plt.margins(0)
        plt.xlabel(u"迭代次数")  # X轴标签
        plt.ylabel(u"X2")  # Y轴标签
        plt.title(u"X2识别曲线")  # 标题

        plt.show()

if __name__ == '__main__':
    time = 30
    size = 10
    dimension = 2
    v_low = -0.1
    v_high = 0.1
    low = [-2*np.pi,-2*np.pi]
    up = [2*np.pi, 2*np.pi]
    pso = PSO(dimension, time, size, low, up, v_low, v_high)
    pso.pso()

参考（CX）链接：

粒子群优化算法(Particle Swarm Optimization, PSO)的详细解读 - 知乎 (zhihu.com)

一文搞懂什么是粒子群优化算法(Particle Swarm Optimization，PSO)【附应用举例】 - 知乎 (zhihu.com)