常用激活函数及偏导

常用激活函数及偏导

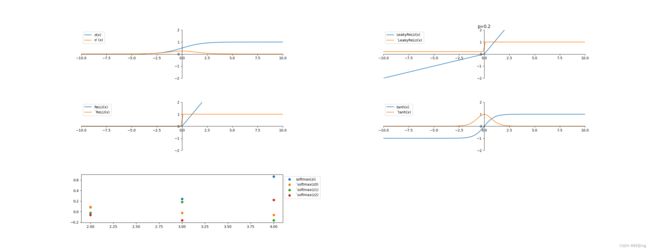
derivative.py

import numpy as np
import matplotlib.pyplot as plt

plt.subplots_adjust(hspace=0.5 , wspace=0.5)
rows = 3
cols = 2

def plot_style(ax):
    # 设置轴隐藏
    ax.spines['top'].set_visible(False) 
    ax.spines['right'].set_visible(False)
    # 设置轴位置
    ax.spines['bottom'].set_position(('axes', 0.5))
    ax.spines['left'].set_position(('axes', 0.5))
    # 设置刻度间隔
    # ax.xaxis.set_major_locator(plt.MultipleLocator(1))
    # ax.yaxis.set_major_locator(plt.MultipleLocator(1))
    # 设置刻度范围
    plt.xlim(-10,10)
    plt.ylim(-2,2)

# --------------------------------------

x=np.linspace(-10,10,100)

def Sigmoid(x) :
    a = 1/(1+np.exp(-x))
    return a

def d_Sigmoid(x):
    a = Sigmoid(x)*(1-Sigmoid(x))
    return a

graph = plt.subplot(rows,cols,1)
plot_style(graph)
plt.plot(x,Sigmoid(x),label="σ(x)")
plt.plot(x,d_Sigmoid(x),label="σ`(x)")
# plt.title('σ(x) & σ`(x)=σ(1-σ)')
plt.legend()

# plt.show()

# --------------------------------------
def LeakyReLU(x,p):
    cond = x>=0
    a = np.where(cond,x,p*x) 
    return a 
def d_LeakyReLU(x,p):
    cond = x>=0
    a = np.where(cond,1,p) 
    return a 

x=np.linspace(-10,10,100)
graph = plt.subplot(rows,cols,2)
plot_style(graph)
p = 0.2
plt.plot(x,LeakyReLU(x,p),label='LeakyReLU(x)')
plt.plot(x,d_LeakyReLU(x,p),label='`LeakyReLU(x)')
plt.title(f'p={p}')
plt.legend()

# --------------------------------------
def ReLU(x) :
    a = LeakyReLU(x,0)
    return a 

def d_ReLU(x) :
    a = np.array(x,copy=True)
    a[x<0] = 0
    a[x>=0] = 1
    return a 

x=np.linspace(-10,10,100)
graph = plt.subplot(rows,cols,3)
plot_style(graph)
plt.plot(x,ReLU(x),label='ReLU(x)')
plt.plot(x,d_ReLU(x),label='`ReLU(x)')
# plt.title('ReLU(x) & `ReLU(x)')
plt.legend()
# --------------------------------------


def tanh(x):
    a = 2*Sigmoid(2*x) - 1
    return a

def d_tanh(x):
    b = np.power(tanh(x),2) 
    a = 1 - b
    return a

x=np.linspace(-10,10,100)
graph = plt.subplot(rows,cols,4)
plot_style(graph)
plt.plot(x,tanh(x),label='tanh(x)')
plt.plot(x,d_tanh(x),label='`tanh(x)')
# plt.title(' tanh(x) & `tanh(x) ')
plt.legend()
# --------------------------------------

# x=np.linspace(0,10,3)
x = [2,3,4]
def softmax(x):
    expx = np.exp(x)
    a = expx / np.sum(expx)
    return a

def d_softmax(x):
    p = softmax(x)
    count = len(x)
    out = []
    for i in range(count) :
        for j in range(count) :
            ret = 0
            if j==i:
                ret = p[i]*(1-p[j])
                print(f'dp[{i}]/dz[{j}] = p[{i}]*(1-p[{j})] = {ret}')
            else :
                ret = -p[i]*p[j]
                print(f'dp[{i}]/dz[{j}] = -p[{i}]*p[{j}] = {ret}')
            out.append(ret)
    return out

plt.subplot(rows,cols,5)
plt.scatter(x,softmax(x),label=f'softmax(zi)')
d_out = d_softmax(x)
len = len(x)
for i in range(len):
    plt.scatter(x,d_out[len*i:len*(i+1)],label=f'`softmax(z{i})')

plt.legend(loc='upper left', bbox_to_anchor=(1, 1))

# --------------------------------------

plt.show()