剪切散斑包裹相位图的正余弦滤波算法演示实例
一、正余弦滤波算法原理
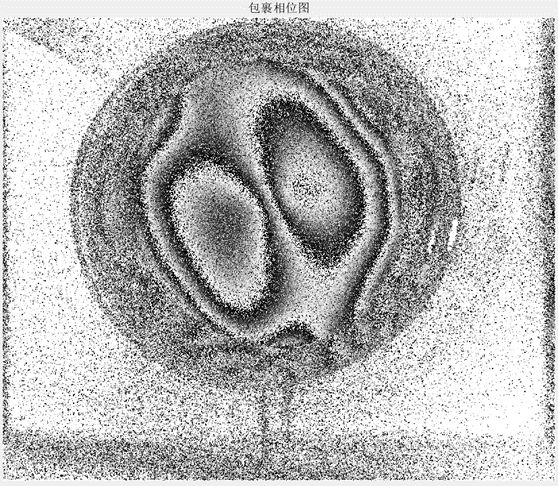
相位图的滤波是还原相位信息的重要过程,因为散斑条纹图中的相位信息包裹在其中,要使得还原真实信息必须经过解包裹,但解包裹的前提是获得去噪的条纹图,否则解包裹过程失败。
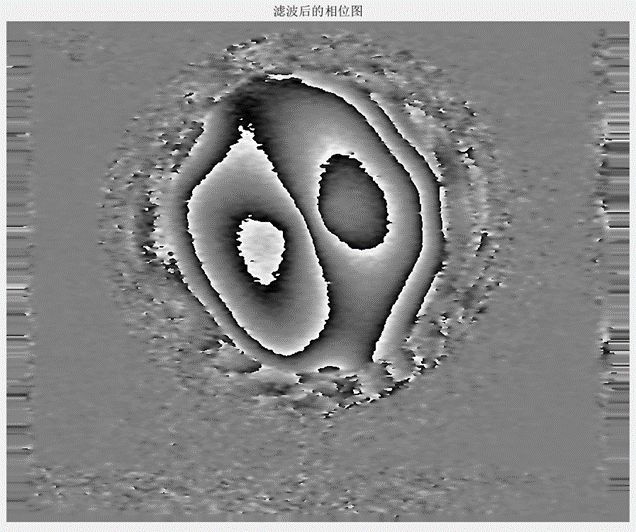
正余弦滤波方法利用正余弦函数的连续性,将条纹图中不连续的相位信息转化为连续值,即相位图分别进行正弦和余弦变换,这样避免了相位图跃变的信息丢失,然后分别进行均值滤波,最后对滤波后的正弦相位图和余弦相位图进行反正切处理,这样可以去掉跃变处的噪声,也可以保留相位信息。
对相位值 Δ ( x , y ) \Delta (x,y) Δ(x,y) 分别作正弦和余弦处理,获得两个连续的分量 s ( x , y ) s\left( x,y \right) s(x,y)、 c ( x , y ) c\left( x,y \right) c(x,y):
{ s ( x , y ) = sin [ Δ ( x , y ) ] c ( x , y ) = cos [ Δ ( x , y ) ] \left\{ \begin{matrix} s\left( x,y \right)=\sin \left[ \Delta (x,y) \right] \\ c\left( x,y \right)=\cos [\Delta (x,y)] \\ \end{matrix} \right. {s(x,y)=sin[Δ(x,y)]c(x,y)=cos[Δ(x,y)]
此时,相位图分成两个分量,再分别采用均值滤波进行计算,以均值滤波中任意像素点(i,j)为中心点,窗口的大小为m×n ,则正弦相位图滤波后为 s ˉ ( x i , y j ) \bar{s}({{x}_{i}},{{y}_{j}}) sˉ(xi,yj),余弦相位值滤波后为 c ˉ ( x i , y j ) \bar{c}({{x}_{i}},{{y}_{j}}) cˉ(xi,yj) ,表示为:
s ˉ ( x i , y j ) = 1 m × n ∑ ( x , y ) ∈ w s ( x , y ) c ˉ ( x i , y j ) = 1 m × n ∑ ( x , y ) ∈ w c ( x , y ) } \left. \begin{matrix} \bar{s}({{x}_{i}},{{y}_{j}})=\frac{1}{m\times n}\sum\limits_{\left( x,y \right)\in w}{s(x,y)} \\ \bar{c}({{x}_{i}},{{y}_{j}})=\frac{1}{m\times n}\sum\limits_{\left( x,y \right)\in w}{c(x,y)} \\ \end{matrix} \right\} sˉ(xi,yj)=m×n1(x,y)∈w∑s(x,y)cˉ(xi,yj)=m×n1(x,y)∈w∑c(x,y)⎭⎪⎬⎪⎫
w表示为m×n中全部像素点。将正余弦分量作反正切处理便获得去噪后的完整相位。
Δ ^ ( x , y ) = arctan [ s ˉ ( x i , y j ) / c ˉ ( x i , y j ) ] \hat{\Delta }(x,y)=\arctan \left[ {\bar{s}({{x}_{i}},{{y}_{j}})}/{\bar{c}({{x}_{i}},{{y}_{j}})}\; \right] Δ^(x,y)=arctan[sˉ(xi,yj)/cˉ(xi,yj)]
二、实例演示
现在有如下图所示的包裹相位图,
三、资源获取
上述资源可从以下链接处获取:
https://download.csdn.net/download/qq_36584460/82370669
资源包含以下内容:
1) 包裹相位图-正余弦演示.mat (包裹相位图)
2) 剪切散斑包裹相位图的正余弦滤波算法剪切散斑包裹相位图的正余弦滤波算法.m(Matlab程序)
四、正余弦滤波算法技术服务
可提供相关的正余弦滤波算法改进技术服务。具体技术服务可私信博主。