Recursive Algorithm
什么是Recursive Algorithm?
A recursive algorithm is a special type of algorithm in which a method calls itself over and over again to solve a problem. Each successive call reduces the complexity of the problem and moves closer and closer to a solution until finally a solution is reached, the recursion stops, and the method can exit.
递归算法就是不断调用自己使得复杂问题不断趋近与被解决, 当问题被解决就停止递归。
可以看出递归算法的要素是,
1. 调用自己
2. 每次调用,要趋近问题解决
3. 问题解决退出
Remember, the objective of a recursive algorithm is to break a complex problem into a smaller more manageable problem.
所以,递归算法要够简洁,否则就要重新思考你解决问题的思路。
Parts of a Recursive Algorithm
- base cases, 就是出口点, 包括条件判断和退出两部分
- recursion, 调用自己
- work. 除了base cases 和 recursion 的其他部分
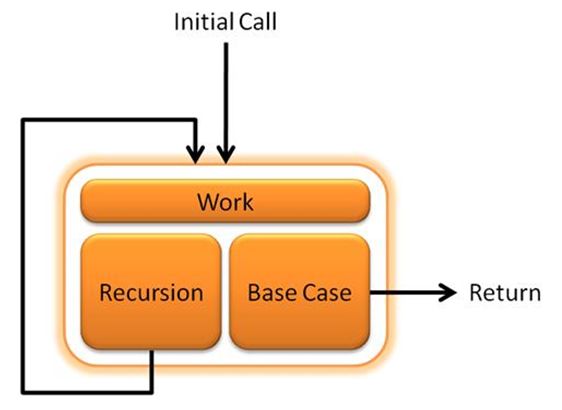
示例:
 代码
代码
2 {
3 Console.WriteLine(number);
4 if (number == 0 )
5 {
6 return ;
7 }
8 else
9 {
10 CountDown(number - 1 );
11 }
12 }
Line 3 是work;Line4~7是base cases;line 10是Recursion
或者这样写也是一样的。base cases不如上面的明显,其实一样,number=0也是要退出。
We can still stay, the base case occurs when the number parameter is zero.
2 {
3 Console.WriteLine(number);
4 if (number > 0 )
5 {
6 CountDown(number - 1 );
7 }
8 }
Winding and Unwinding
Winding is simply the work that occurs before a recursive call, and unwinding is the work that occurs after the recursive call.
比较:
 代码
代码
1 public void CountDown( uint number)
2 {
3 Console.WriteLine(number);
4 if (number > 0 )
5 {
6 CountDown(number - 1 );
7 }
8 }
// UnWinding
1 public void CountUp( uint number)
2 {
5 if (number > 0 )
6 {
7 CountUp(number - 1 );
8 }
9 Console.WriteLine(number);
10 }
执行CountDown(5),结果是5,4,3,2,1,0;
执行CountUp(5), 结果是0,1,2,3,4,5;
记住, the location of “the work” in a recursive algorithm can affect the timing of when it is executed.
Six Steps to Writing a Recursive Algorithm
In attempt to make writing recusive algorithms a bit more approachable, I’ve broken the process down into the following six steps:
- Define the Inputs
You have to start somewhere, and when it comes to methods a good place to start is the method signature. So the first thing you need to do is determine the inputs with which you need to work because these will become your method parameters. Once you know that, you can pick a good name for the method write your method signature. - Define the Base Cases
The FIRST thing you should do after defining your method signature is to identify the base cases for your recursive algorithm and get them into your code. The BIGGEST problem I see when people are trying to solve a problem with recursion is that they start on the recursive part. Base cases are simple. Start by getting the simple part out of the way.
先从Base case开始,而不是从递归部分开始! - Think Backwards from the Base Case
Some solutions for recursive problems will come to you naturally. Some will stump you. If you find yourself stumped, start from the base case and work backwards. Recursion is a very nebulous thing, so if you start thinking about the recursion then you’re mind is going to explode. A base case is a very well-defined and concrete concept. If you start with the base cases and work backwards, then you are starting from a concrete concept and it’s easier to think though. Most of the people I see having major problems with seemingly simple recursive problems are starting at the wrong end of the problem. - Define the Recursion
If you are writing a recursive function then you are going to need to recurse at some point, so you need to identify how a recursive call plays into the solution. You also need to identify how the inputs to the recursive method calls need to change to ensure you are moving towards a base case.
每一步Recursion都要保证,距离问题解决,base case(出口) 越来越近! - Do the Work
Remember, recursion is about working towards a base case, so the method needs to continually move in that direction with the work it does. You may also need to complete other operations along the way that are part of the solution but have absolutely nothing to do with moving towards a base case. - Don’t get complicated
Recursive algorithms tend to be elegantly simple, so if you find yourself doing crazy stuff to get a recursive algorithm to work then you’re probably doing something horribly wrong; especially in an interview. If you find yourself needing a bunch of variables to store stuff, or you suddenly get the urge to introduce a delegate or anonymous function into the mix, then you probably need to backtrack.
A Quick Dive into the Recursive Factorial Function
Problem:
0! = 1
n! = n * (n-1)!
Factorial sounds like a great name for the method. Second, we know that the factorial function accepts a single integer as an input, and returns and integer value. As such, let’s go ahead and create the following method signature:
public int Factorial(int n)
{
}
Next, we need to incorporate the base case into the method. Look back at the mathematical definition for factorials. There are two definitions. One uses recursion. One does not. Guess which one is the base case? If you guessed the first one, then you are right.
public int Factorial(int n)
{
if(n==0) return 1;
}
Look problem, you will see that the recursive part of the algorithm has been laid out for us fairly well. It’s simply a matter of getting the equation translated into code.
01 public int Factorial(int n)
02 {
03 if(n==0) return 1;
04 return n * Factorial(n-1);
05 }
Now we have a functioning, recursive Factorial function. Fortunately, most interview questions involving recursion center on mathematical concepts like Factorials and Fibonacci numbers.
Show Off for an Interview
01 public UInt64 Factorial(byte n)
02 {
03 return n==0 ? 1 : n * Factorial(n-1);
04 }
a few key differences: the body is on a single line,
1. it makes use of the conditional operator instead of an if statement,
2. it uses an unsigned long integer as the return value
3. and a byte as the input parameter instead of integers.
使用int作为返回值, the method will crap out at Factorial(17) because the result is larger than an integer.
A long value gets you all the way to Factorial(20).
And the Uint64 allows you to go all the way up to Factorial(65) before you encounter issues.
Since the method quits working when you pass in 65, an int value is overkill. A short value is overkill too. So you use a byte.
Fibonacci
Pseudocode
function fib is:
input: integer n such that n >= 0
1. if n is 0, return 0
2. if n is 1, return 1
3. otherwise, return [ fib(n-1) + fib(n-2) ]
end fib
Refer to:http://blog.chinaunix.net/u/16292/showart_496723.html
递归的方法,时间复杂度O(N^2); 递推的方法,时间复杂度O(N)
打靶问题
这个问题有点变态,不容易轻易理解解决。
问题是:10枪打90环,求所有可能组合?
Ref: http://www.cnblogs.com/lds85930/archive/2007/07/05/807198.html
DataStructure_Algorithm/Recursive/
