【数据结构】顺序表

目录

顺序表的概念

顺序表分类

静态顺序表

动态顺序表

数据的初始化

顺序表的销毁

数据的插入和删除

数据的查找

全部代码演示

---

顺序表的概念

顺序表是用一段物理地址连续的存储单元依次存储数据元素的线性结构，一般采用数组存储，在数组上完成数据的增删查改。

顺序表分类

静态顺序表

使用定长数组存储元素

#define N 10
typedef int SLDataType;
struct SeqList 
{
	SLDataType a[N];
	int size;
};

静态顺序表最大的弊端：就是它的大小不确定：空间开多了浪费，开少了不够用

动态顺序表

使用动态开辟的数组存储

动态顺序相比较优点就是按需申请

我们接下来重点介绍动态顺序表如何实现数据的增删查改

typedef int SLDataType;
struct SeqList 
{
	SLDataType* a;
	int size;//有效数据个数
	int capacity;//空间容量
};

数据的初始化

首先，我们对数据进行初始化，封装一个SeqInit函数，我们可以像下面这样初始化

void SeqInit(SL s) {
	s.a = NULL;
	s.size = 0;
	s.capacity = 0;
}

当然我们也可以在一开始开辟一段空间

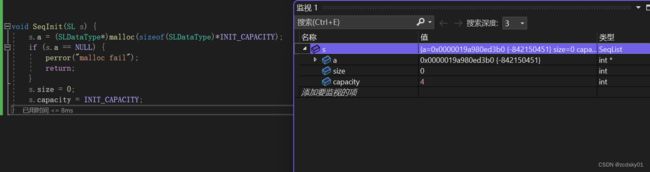
void SeqInit(SL s) {
	s.a = (SLDataType*)malloc(sizeof(SLDataType)*INIT_CAPACITY);
    //INIT_CAPACITY表示初始化容量为4
	if (s.a == NULL) {
		perror("malloc fail");
		return;
	}
	s.size = 0;
	s.capacity = INIT_CAPACITY;
}

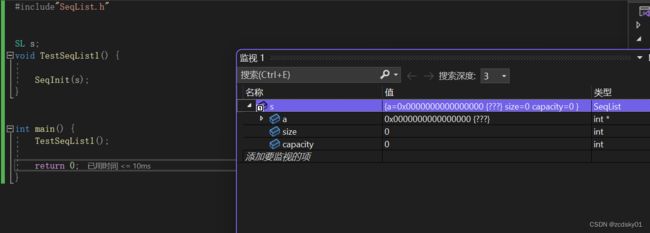
 我们调试一下观察初始化结果，发现好像初始化成功了，但是我们在test.c文件再看看

 

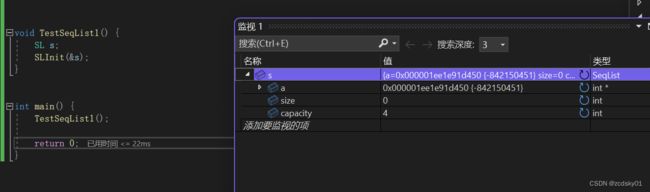
我们会惊讶的发现没有初始化成功，这又是为什么呢，答案很简单，我们在初始化时犯了一个低级错误，当我们想要修改某一块内存是需要用的是传址调用，但我们调用SeqInit函数时用的是传值调用，修改一下

 这样我们就初始化成功了（我在修改函数参数时也修改了一下函数名，老铁们不要看错哦）

顺序表的销毁

接下来是顺序表的销毁也很简单

void SLDestroy(SL* ps)
{
	free(ps->a);
	ps->a = NULL;
	ps->capacity = ps->size = 0;
}

数据的插入和删除

然后接下来就是数据的插入和删除，分为头插，头删，尾插，尾删，顾名思义我们需要封装对应的函数

void SLPushBack(SL* ps, SLDataType x);//尾插
void SLPopBack(SL* ps);//尾删
void SLPushFront(SL* ps, SLDataType x);//头插
void SLPopFront(SL* ps);//头删

 我们先来看尾插：很多人会写成如下代码，那么对不对呢

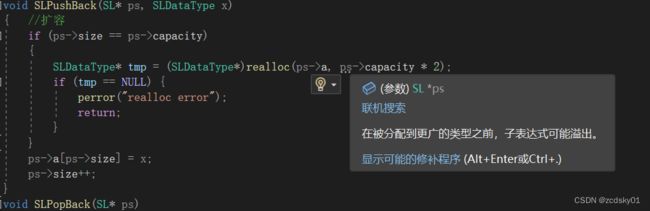
void SLPushBack(SL* ps, SLDataType x)
{   //扩容
	if (ps->size == ps->capacity)
	{
		SLDataType* tmp = (SLDataType*)realloc(ps->a, ps->capacity * 2);
		if (tmp == NULL) {
			perror("realloc error");
			return;
		}
	}
	ps->a[ps->size] = x;
	ps->size++;
}

 我们把鼠标放到ps处会发现给出我们一句话，在分配到更广的类型前，子表达式可能溢出

什么意思呢， 简单来说就是扩容扩少了，当前容量是4，你要扩充到8，每一个类型是SLDataType，也就是一次需要32个字节，但是你写的是capacity*2只有8个字节，所以需要做如下修改：再乘上sizeof(SLDataType)

 SLDataType* tmp = (SLDataType*)realloc(ps->a,sizeof(SLDataType) * ps->capacity * 2);

 然后就是尾删，这个比较简单

void SLPopBack(SL* ps)
{   //温柔检查
	if (ps->size == 0)
		return;
	//暴力检查(断言)
	//assert(ps->size > 0);
	ps->size--;
}

接下来就是头插：（因为头插时也需要考虑扩容，所以我们直接将之前写的扩容函数封装起来，进行调用）对应的扩容和头插函数如下

void SLPushFront(SL* ps, SLDataType x)
{
	assert(ps);
	SLCheckCapacity(ps);
	int end = ps->size - 1;
	while (end >= 0)
	{
		ps->a[end + 1] = ps->a[end];
		end--;
	}
	ps->a[0] = x;
	ps->size++;
}
void SLCheckCapacity(SL* ps) {
	assert(ps);
	//扩容
	if (ps->size == ps->capacity)
	{
		SLDataType* tmp = (SLDataType*)realloc(ps->a, sizeof(SLDataType) * ps->capacity * 2);
		if (tmp == NULL) {
			perror("realloc error");
			return;
		}
		ps->a = tmp;
		ps->capacity *= 2;
	}
}

然后就是头删：

void SLPopFront(SL* ps)
{
	assert(ps);
	assert(ps->size > 0);
	int begin = 1;
	while (begin < ps->size)
	{
		ps->a[begin - 1] = ps->a[begin];
		++begin;
	}
	ps->size--;
}

但是呢，对比头插头删，尾插尾删,我们会发现头插头删效果并不好

头插/头删时间复杂度为：O(N^2)

尾插/尾删时间复杂度为：O(N)

如果我们想要在某个位置插入数据怎么办，很简单，那我们再创建一个函数：

void SLInsert(SL* ps, int pos, SLDataType x) {
	assert(ps);
	assert(pos >= 0 && pos<=ps->size);
	SLCheckCapacity(ps);
	int end = ps->size - 1;
	while (end >= pos)
	{
		ps->a[end + 1] = ps->a[end];
		--end;
	}
	ps->a[pos] = x;
	ps->size++;
}

 我们可以发现如果有了这个函数，我们完全不需要头插，尾插函数，因为它们对应的参数，实际就是pos=0和pos=size时，所以头插尾插函数体可以调用该函数。

中间位置删除函数如下：（同理，尾删头删都可直接调用该函数）

void SLErase(SL* ps, int pos) {
	assert(ps);
	assert(pos >= 0 && pos size);
	int begin = pos + 1;
	while (begin < ps->size)
	{
		ps->a[begin - 1] = ps->a[begin];
		++begin;
	}
	ps->size--;
}

数据的查找

最后呢就是查找，很简单

int SLFind(SL* ps, SLDataType x) {
	assert(ps);
	for (int i = 0; i < ps->size; i++)
	{
		if (ps->a[i] == x)
			return i;
	}
	return -1;
}

全部代码演示

至此关于顺序表的内容就结束了，下面附上全部代码：

SeqList.h

#include
#include
#include
#define INIT_CAPACITY 4
typedef int SLDataType;
typedef struct SeqList 
{
	SLDataType* a;
	int size;//有效数据个数
	int capacity;//空间容量
}SL;
//增删查改

void SLInit(SL* ps);//初始化
void SLDestroy(SL* ps);//销毁
void SLPushBack(SL* ps, SLDataType x);//尾插
void SLPopBack(SL* ps);//尾删
void SLPushFront(SL* ps, SLDataType x);//头插
void SLPopFront(SL* ps);//头删
void SLPrint(SL* ps);
void SLCheckCapacity(SL* ps);//扩容
void SLInsert(SL* ps, int pos, SLDataType x);//中间位置插入
void SLErase(SL* ps, int pos);//中间位置删除
int SLFind(SL* ps, SLDataType x);//查找

SeqList.c

#include"SeqList.h"


void SLInit(SL* ps) {
	assert(ps);
	ps->a = (SLDataType*)malloc(sizeof(SLDataType)*INIT_CAPACITY);
	if (ps->a == NULL) {
		perror("malloc fail");
		return;
	}
	ps->size = 0;
	ps->capacity = INIT_CAPACITY;
}
void SLDestroy(SL* ps)
{
	assert(ps);
	free(ps->a);
	ps->a = NULL;
	ps->capacity = ps->size = 0;
}
void SLPrint(SL* ps)
{
	assert(ps);
	for (int i = 0; i < ps->size; i++) {
		printf("%d ", ps->a[i]);
	}
	printf("\n");
}
void SLPushBack(SL* ps, SLDataType x)
{   
	assert(ps);
	//扩容
	SLCheckCapacity(ps);
	ps->a[ps->size] = x;
	ps->size++;
}
void SLPopBack(SL* ps)
{   //温柔检查
	//if (ps->size == 0)
	//	return;
	//暴力检查(断言)
	assert(ps->size > 0);
	ps->size--;
}
void SLPushFront(SL* ps, SLDataType x)
{
	assert(ps);
	SLCheckCapacity(ps);
	int end = ps->size - 1;
	while (end >= 0)
	{
		ps->a[end + 1] = ps->a[end];
		end--;
	}
	ps->a[0] = x;
	ps->size++;
}
void SLCheckCapacity(SL* ps) {
	assert(ps);
	//扩容
	if (ps->size == ps->capacity)
	{
		SLDataType* tmp = (SLDataType*)realloc(ps->a, sizeof(SLDataType) * ps->capacity * 2);
		if (tmp == NULL) {
			perror("realloc error");
			return;
		}
		ps->a = tmp;
		ps->capacity *= 2;
	}
}
void SLPopFront(SL* ps)
{
	assert(ps);
	assert(ps->size > 0);
	int begin = 1;
	while (begin < ps->size)
	{
		ps->a[begin - 1] = ps->a[begin];
		++begin;
	}
	ps->size--;
}
void SLInsert(SL* ps, int pos, SLDataType x) {
	assert(ps);
	assert(pos >= 0 && pos<=ps->size);
	SLCheckCapacity(ps);
	int end = ps->size - 1;
	while (end >= pos)
	{
		ps->a[end + 1] = ps->a[end];
		--end;
	}
	ps->a[pos] = x;
	ps->size++;
}
void SLErase(SL* ps, int pos) {
	assert(ps);
	assert(pos >= 0 && pos size);
	int begin = pos + 1;
	while (begin < ps->size)
	{
		ps->a[begin - 1] = ps->a[begin];
		++begin;
	}
	ps->size--;
}
int SLFind(SL* ps, SLDataType x) {
	assert(ps);
	for (int i = 0; i < ps->size; i++)
	{
		if (ps->a[i] == x)
			return i;
	}
	return -1;
}

文章到这就结束了，觉得学到些东西的老铁，点个关注，写个评论呗，留痕，我们下一篇再见！