RobinKarp(字符串哈希)---分析与实现(C++)

1. 简述

给定字符串pattern和串text。求串pattern在串text中出现的位置。

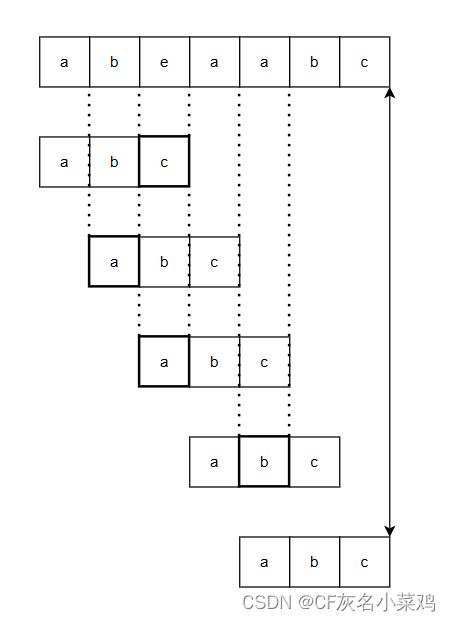
暴力比较是逐个字符比较来确定两个串是否相等，若当前比较失败

则回到开始字符对应字符的后一个字符重复过程。

哈希就是一个大范围到小范围的映射

字符串哈希则是通过比较两个串的哈希值相等来判断两个字符串是

否相等，如果每次都要像暴力字符匹配那样重新计算哈希值的话，

那么复杂都就太高了。所以这里用到了一种技巧：滚动哈希。

2. 滚动哈希

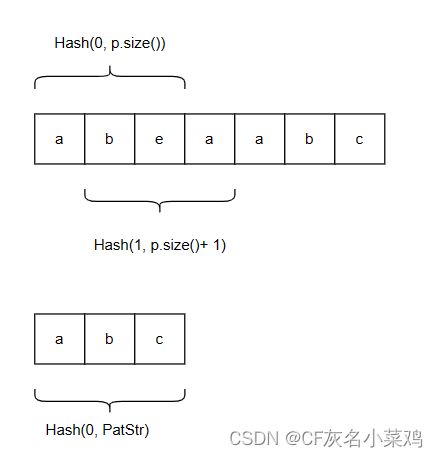
由上面的图可以知道，要让字符串哈希求值快，则需要

Hash(0, p.size)到Hash(1, p.size + 1)的转换快。

所以我们这里直接自然想到了，进制的表示。

所以我们很自然的定义哈希函数

$$H(str)=a^{0}str[0]+a^{1}str[1]...+a^{str.size()}str[str.size()-1]$$
则
$$H(0,pat.size()-1)=H(str)H(1,pat.size()-1)=H(str)-str[0]$$
推导式
$$H(1,str.size())=(H(str)-str[0])/base+a^{pat.size()-1}\ast str[str.size()]$$

3. 更进一步

如果直接这样运算的话，H(str)的值会随着字符串长度的增加而呈指数级的增长。我

们希望值落在一个区间，所以通常会模上一个数使得哈希值在给定区间。

$$a\%p=c<=>a=kp+c(0<c<p)$$

因为我们无法从

$$(\sum _{i=1}^{p.size-1}{base}^{i}txt[i])\%MOD$$

推出
$$(\sum _{i=1}^{p.size-1}bas{e}^{i-1}txt[i])\%MOD$$
因为
$$a\ast b\%MOD=(a\%MOD)\ast (b\%MOD)\%MOD$$
成立，而

$$a/b\%MOD\ne (a\%MOD)/(b\%MOD)\%MOD$$

所以原来的哈希函数不行，而我们反着来的时候就可以了。

$$H(0,p.size-1)=\sum _{i=0}^{p.size-1}bas{e}^{p.size-1-i}\ast str[i]$$
此时的H(0, p.size - 1)到H(1, p.size)推导式为

$$H(1,p.size)=\{(H(0,p.size-1)-(str[0]bas{e}^{p.size-1}\%MOD)+MOD)\%MOD\ast base+str[p.size]\}\%MOD$$
所以我们应该先求出$bas{e}^{p.size-1}\%MOD$

求模运算时要特别注意是否有相减为负数的情况。

3. 实现

#include 

#include 
#include 

#include 

int robinKarp(const char *pat, const char *txt, uint8_t base)
{
    if (!pat || !txt || !base)
        return -1;

    int pLen = (int) strlen(pat);
    int tLen = (int) strlen(txt);
    int MOD = 251;

    if (pLen > tLen)
        return -1;

    int patHashVal = 0;

    int mem_base = 1;
    int cTxtHashVal = 0;


    for ( int i = 0; i < pLen; ++i) {
        cTxtHashVal += mem_base * txt[ pLen - 1 - i ] ;
        patHashVal += mem_base * pat[ pLen - 1 - i ];
        cTxtHashVal %= MOD;
        patHashVal %= MOD;

        if ( i + 1 != pLen)
            mem_base = (mem_base * base) % MOD;
    }
    if (cTxtHashVal == patHashVal)
        return 0;

    for ( int i = pLen;i < tLen; ++i) {



        cTxtHashVal = (cTxtHashVal - (mem_base * txt[i - pLen])%MOD + MOD)%MOD;
        cTxtHashVal = (cTxtHashVal * base + txt[i]) % MOD;

        if (cTxtHashVal == patHashVal) {
            //printf("%d\t", i - pLen + 1);
             return i - pLen + 1;
        }
    }

    return -1;
}

int main( int argc, char **argv)
{

    std::string txt("abeaabcabc");
    std::string pat("abc");


    int ret = robinKarp(pat.c_str(), txt.c_str(), 255);

    if ( -1 != ret ) {
        std::cout << "match pos: " << ret << std::endl;
    }

    return 0;
}

4. ref

brilliant
geekforgeeks