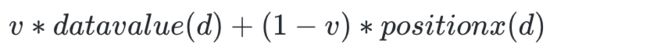可视化论文精读系列:Relaxed Dot Plots
论文题目:《Relaxed Dot Plots: Faithful Visualization of Samples and Their Distribution》
论文作者:Nils Rodrigues; Christoph Schulz; Soren Doring; Daniel Baumgartner; Tim Krake; Daniel Weiskopf
主创来自德国斯图加特大学可视化研究中心
该研究中心研究方向:
科学可视化:数字人文、评估、显微可视化、网络与网络安全、社交媒体
信息可视化及可视分析:生物信息学可视化、视频流的可视分析、基于纹理的流可视化....
图形学:基于图像的场景表示、模拟摄影、结构光在移动设备上的扫描...
相关概念
什么是Dot Plot?
Dot Plot(点图),又称为点阵图,是一种简单的数据可视化形式。由x轴和y轴的图形上绘制为点的数据点组成,用于以可视化方式表示某些数据趋势或数据分组。
点图有两种形式:
利兰·威尔金森点阵图:
第一种是由利兰·威尔金森(Leland Wilkinson)描述的,它是一种在手绘(前计算机时代)图表中用来描述分布的图表。可以理解为在bar chart中填充数据点,以同时展示分组数据的总量差异和个体描述。这种编码方式既实现了数据表示的「可数性」和「精确性」,又体现了数据的频率。但其局限性在于当数据量较大时,点阵图会显得杂乱不堪。
利兰·威尔金森点阵图遵循4个绘制原则:
R1: 数据值与点一一对应
R2: 所有点大小相同
R3: 位置和数据值的对应要准确
R4: 点必须对齐堆叠
威廉·克利夫兰(ggplot作者)点阵图:
另一个版本被威廉·克利夫兰(ggplot作者)描述为Bar Chart的替代品,图中的点被用来描述与分类变量相关的量化值。这种编码方式的好处是减少了「Data Ink」,增加了信息表达的效率。
点图的具体应用可以参考 :点图指北
什么是NonLinear Dot Plot?
基于列布局,将点的大小与该列的数据频率值映射,有利于异常检测。
什么是moire ́ effects(莫尔效应)?
moire ́ effects,“莫尔效应”又被称为“波纹效应”、“莫瑞效应”。两个重叠的线条形态所产生的干扰中,会生成一种波纹团。“莫尔效应”会严重影响可视化的数据呈现能力。
Dot Plot和Bar Chart
Bar Chart缺点:相比之下,Bar Chart将汇总后的统计值进行可视化编码,但这种统计通常会导致数据的不真实表示,在稀疏数据中尤为明显。所以,Bar Chart只负责展示汇总,而不理会内部的分布。
Dot Plot缺点:对于较小的数据集,传统的Dot Plot更具优势,但在处理较大的数据集和不同的数据频率时,直方图可以轻松的利用数学方式进行矩形高度的调整,无须更改band。但Dot Plot是非线性缩放的,会增强moire ́ effects效应。此外,强制点进入列中的传统布局可能会错误地表示真实的数据值。
研究动机
传统列布局Dot Plot带来的moire ́ effects如何避免?
传统列布局Dot Plot带来的真实数据与实际位置的误差如何减少?
传统列布局Dot Plot边界不光滑问题如何解决?
研究成果
摒弃传统列布局为基础的Dot Plot,将点更正确、更美观地放置在封闭空间中。
一项数学描述
从严格对齐的非线性点图过渡到relaxed 变体的数学描述。
一个布局算法
扫描式的、基于Lloyd松弛来提高位置的正确性、并建立蓝色噪声的算法。
(算法已开源:https://github.com/NilsRodrigues/relaxeddotplots)
一个评估研究
正确性、蓝色噪声、可读性。(研究表明,性能优于传统Dot Plot)
相关研究
基于Dot的可视化
Bee swarm plots 蜜蜂图
抖动的一维散点图,将可能的点分开,使每个点都可见。
https://cran.r-project.org/web/packages/beeswarm/index.html
https://github.com/aroneklund/beeswarm
https://cran.r-project.org/web/packages/ggbeeswarm/vignettes/usageExamples.pdf
https://www.jianshu.com/p/30892c26d0e9
BNP蓝色噪声图
抖动的二维散点图,在偏移位置上做了优化。
van Onzenoodt C, Singh G, Ropinski T, et al. Blue Noise Plots[C]//Computer Graphics Forum. 2021, 40(2): 425-433.
使用蓝色噪声属性绘制二维标量场
Görtler J, Spicker M, Schulz C, et al. Stippling of 2D scalar fields[J]. IEEE transactions on visualization and computer graphics, 2019, 25(6): 2193-2204.
stippling点缀着色
基于dot的可视化绘制模式不仅应用在上述所说的信息可视化当中,在医疗、建筑等模拟真实世界的图像转化中也有体现。主要是将图像中的色域转换为聚合粒子的形式,以此突出图像的轮廓。
Lu A, Morris C J, Ebert D S, et al. Non-photorealistic volume rendering using stippling techniques[C]//IEEE Visualization, 2002. VIS 2002. IEEE, 2002: 211-218.
Schulz C, Kwan K C, Becher M, et al. Multi-class inverted stippling[J]. ACM Transactions on Graphics, 2021, 40(6).
Blue Noise Property 蓝色噪声
一些对点进行松弛布局的算法,比较著名的是Lloyd算法 和更通用的 Linde-Buzo-Gray算法。后者可以推断样本数量,因为在Dot Plot中样本数量固定,所以本文基于前者进行改进。
Kernel Density Estimation (KDE) 核密度估计
核密度函数用于估计密度函数,本文通过改进核密度估计来确定轮廓,后文有说明。在此不赘述。
目标和总览
目标:更准确、更美观的Dot Plot:
目标一:点具有更少的位置误差
即x轴上的实际显示位置与真实数据值之间的差异。
目标二:轮廓更好地代表数据频率
即轮廓的峰值、低谷、曲率等特征应该与真正的频率分布相匹配。
目标三:点在轮廓的封闭空间中有更好的布局
即合理打包、点之间没有重叠、并避免未经数据备份的模式。
总览:轮廓计算和Dot布局
第一阶段:轮廓计算
描述了如何确定点的非线性大小以及必要的绘图空间和形状。
确定光滑的轮廓:与KDE类似,使用核函数来准确平稳地估计数据分布。
点的缩放:垂直缩放分布,以满足非线性大小的点的空间要求。并且不强制列布局。
第二阶段:Dot布局
使用改进的Lloyd算法(增加一些位置调整和交换),对点进行放松。
轮廓和点的大小计算
PLOTTING SPACE, SHAPE, AND DOT SIZE
Kernel Frequency Estimation (KFE) 算法:确定轮廓
算法基于核密度估计(KDE)算法改进,KDE算法是在概率论中用来估计未知的密度函数,属于非参数检验方法之一。
算法公式:独立同分布F的n个样本点,设其概率密度函数为f,核密度估计为以下:
K(.)为核函数(非负、积分为1,符合概率密度性质,并且均值为0)。
有很多种核函数,uniform,triangular, biweight, triweight, Epanechnikov,normal等。
核密度估计算法分为平滑内核和不平滑内核:
不平滑内核:直方图。传统的直方图密度估计方法得到的函数不光滑,而且取不同子区间宽度对结果影响很大,比如下图左一和右一。
平滑内核:不同bandwidth和不同核函数的选择,会造成结果的不同。
如下图左二、右二、左三、右三。
BandWidth的选择:经验值,bandwidth = 2 * 直径
核函数的选择:理论上任何积分约为1核函数都可以,本文使用的高斯函数
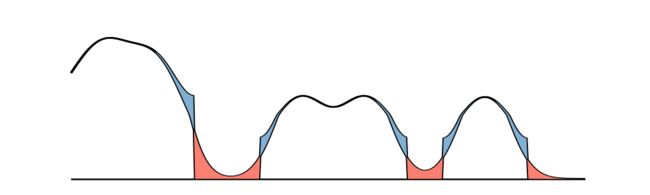
增加「反射」:反射值 = 数据值±半径
对于频率过低的地方,采用反射的方法,增加空间,防止出现断点,导致轮廓不光滑。
初次确定轮廓
过低的值导致空间的不连续
增加反射以避免不连续
Nonlinear Frequency Scaling: 缩放点
上面的方法帮助我们得到了可以用于线性点图的轮廓,但对于非线性点图,要考虑局部点的缩放,以此绘制出具有局部概率相对意义的点,这样绘制出的点可以方便查找异常值。
为了保证缩放前与缩放后的数据分布基本保持不变,也就是满足数据的准确性。
Individual Dot Diameter:确定单个点的直径
为了避免相近位置之间的点直径也相近,并且出现莫尔效应,对每个点的直径再做一次处理。
具体的方式是将直径的大小与位置建立关联。
Dot布局
DOT PLACEMENT
算法流程:垂直交换点的顺序避免倾斜效应,位置交换避免阻塞,位置调整减少数据与位置的误差。
输入:轮廓s,数据列信息c:其中包含中心位置、包含的点和基础数据,x位置上的权重w
输出:dot的位置
交换c中各个点垂直顺序,得到c'
垂直挤压c′中的点,以适应s的边缘, 得到c′′
从c′′中提取点位置和底层,值得到d
repeat
位置交换 TunnelSwaps(d)
质心与s对齐 Lloyd's algorithm
位置调整 v*datavalue(d) + (1-v) * positionx(d)
until d'和d的位置差异 <= 临界值
交换垂直顺序
Alternating Vertical Order
数据本身的顺序排列导致小点在下,大点在上,出现了倾斜效应。如上图左所示。
为了消弭这种效应,点按交替顺序垂直排序。首先,代表最小值的点,然后是最大的值,其次是第二小值,第二大值等。为了保持相同的颜色处于相同的区域,这里只对相同颜色的点进行重新排序。
Centroidal Voronoi Tessellation (CVT) 算法:均匀分布
Voronoi图能够按照原始点所在的位置,将空间划分成不同的区域。如果该区域被限制在一个有限的域中(如一个正方形),那么这些划分的区域全部都是封闭区域。与之对应的,我们能够将所有的边求对偶,得到一个三角刨分,如下图所示:
这种对有限区域的划分是按照输入的点的位置进行的,得到的Voronoi面片是不规则的,每个面片的形状与面积都有较大差距,且对应的三角化也不好(钝角三角形过多,不满足空圆条件)。
是否可以通过对这些原始点的位置进行优化,来得到一个Voronoi面片更一致,三角化结果更好的结果呢?这就是Centroidal Voronoi Tessellation算法的基本问题。
CVT的经典方法是Lloyd's Relaxationhttps://www.jasondavies.com/lloyd/。它可以构建均匀分布的分片。为了避免分片后,出现上图左中的分裂情况,在之前确定轮廓的时候bandwidth取2 * 直径。
在实验迭代后,ε = 0.015、Ε = 0.003可以在更短的时间内获得更精致的布局。
同一分区内的位置调整
Placement Correction
本文目标是创建更加准确的可视化,也就是点的位置要更加接近其真实数据值所映射的位置。所以要在此做位置的调整,以此同时兼具美学性和正确性。
误差的计算方式:考虑点本身的大小
误差指的是实际位置与真实数据值之间的差异,在这里作者强调衡量误差的方式需要考虑点本身的大小,比如:某两个点都偏移了5个像素,其中一个直径为20像素,另一个直径为3像素,后者的视觉误差要大得多。
误差的计算方式:引入平方差
相比之下,小的位置偏移视觉上不容易察觉,所以用平方差来计算位置偏差能够惩罚大的位置偏移,削弱小的位置偏移。
位置调整:选取正确的v值
v是接近正确位置的权重。如果v过大,实际位置过于接近数据值,会导致点的重叠,如下图(d)。如果权重过小,实际位置不接近数据值,如图(b),则违背了正确的可视化原则。为了在正确性和美学性之间平衡,在调试下,v选择0.3最佳,如图(c)。
不同分区间的位置交换
在同一分区内做位置调整可以减少整体的数据误差,但如果某个区域的点过多,就会引起阻塞。
而如果在不同区域间的点进行位置交换,就可以避免这种阻塞,但交换要遵循:点在视觉上的差别小,比如颜色相似,填充图像相似。
效果对比
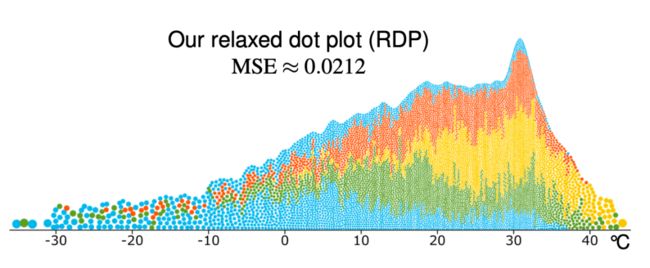
最后论文通过德国气象局网站检索的全球气温测量结果可视化效果对比。
德国气象局网站检索的全球气温测量结果(颜色表示不同月份)
Relaxed Dot Plot
NDP:边缘不光滑
BNP:点不够聚集,不容易比较或发现异常值
BSP:点比较聚集,但未考虑单个子域,所以相同颜色的点比较分散
通过对比,可以看到,使用Relaxed Dot Plot 数据误差小、边缘光滑、颜色分布更均匀。
实验评估Evaluation
正确性Correctness
相比传统的列布局线性点图(NDP),位置误差减少了95%以上。
众包实验(验证可读性)
Crowd-Sourced User Study
通过三个假设检验以下三个方面的效果:位置误差、局部方差、全局数据分布
位置误差
假设一:位置误差低于对照组
用户操作:选择高亮点更接近的真实数据
局部方差
假设二:局部方差低于对照组
用户操作:选择认为数据相对更大 或 更小的数据
全局数据分布
假设三:全局数据分布优于对照组
用户操作:选择更接近数据分布的轮廓
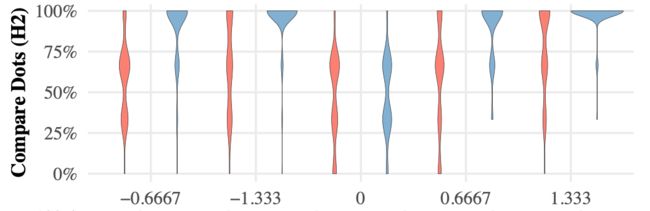
实验分析
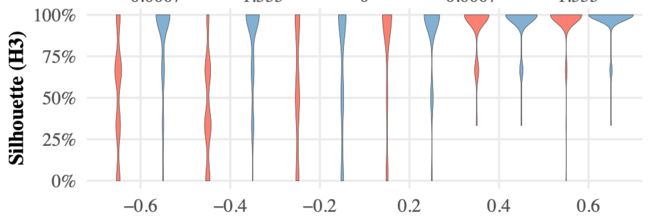
红色 = 基于列布局,蓝色 = relaxed dot plot
从实验结果可以看到:
H2(局部误差)、H3(全局数据分布)具有绝对的正确性。
H1表现一般,用户读到的位置准确率差别不大。但只反映了用户读取的准确率,事实上,因为之前的位置调整算法,Relaxed Dot Plot绘制的准确率高得多。
Blue Noise Property and Moire ́ Effect 蓝色噪声和莫尔效应
relaxed dot plot 没有强烈的噪声,无法捕捉到有规律的频率,莫尔效应被大大削弱。
总结
对单元可视化的借鉴意义
单元可视化是与聚合型可视化存在对立的性质。单元可视化最重要的属性就是身份属性,即对于数据中的每个数据项,在可视化中都有一个相应的视觉标记,且每个视觉标记是与其对应的数据项关联的唯一实体,使得数据项和视觉标记之间保持一对一映射关系。而基于数据聚合的可视化(如条形图,饼图或直方图)则是将多个数据项合并到不可分割的图形实体中。
这篇文章描述的是Dot Plot图表的布局方案,最核心的步骤即确定轮廓 + 内部布局。
确定轮廓,确定的聚合后的轮廓分布。内部布局,确定的是每一个数据项对应的图元位置。
这个过程让我想到了聚合型可视化 -> 单元可视化的变化过程,这个过程往往出现在聚合图元到单元图元的拆解过程中,如果遇到此类场景或许可以借鉴这篇文章的算法。
什么样的数据分析场景可能会用到Relaxed Dot Plot?
展示数据分布
发现单个数据异常值
比如社交媒体场景:
2012 年飓风桑迪期间排名前 100 位的异常转推线程的整体可视化
总体而言,这是一篇算法型文章,从提出问题,算法思路到算法验证,组织结构也比较标准。
Introuduction:概念、当前研究遇到的问题、本文的贡献
related work:三个与研究相关的主题及其现状,以及本文在其基础上做出的改进
Dataset:如果有算法相关的数据集搜集,会在这一部分描述。一般数据集获取方法是爬虫 + 标注评分
overview :算法类型的话是算法的结构,系统类型的话是系统的各个组成部分。
算法步骤xxx or 系统partxxx:算法的话罗列公式及含义,系统的话可视化编码
envaluation:设立假设、对照实验(试用系统后打分/做题) + ttest分析拒拒绝假设
discussion:算法的局限性
future work:总结及未来工作
一篇好的论文:good idea 和写作很重要(好的结构和清晰、母语化的表达)
参考资料
https://www.investopedia.com/dot-plot-4581755
https://cran.r-project.org/web/packages/beeswarm/index.html
https://www.jianshu.com/p/30892c26d0e9
Görtler J, Spicker M, Schulz C, et al. Stippling of 2D scalar fields[J]. IEEE transactions on visualization and computer graphics, 2019, 25(6): 2193-2204.
van Onzenoodt C, Singh G, Ropinski T, et al. Blue Noise Plots[C]//Computer Graphics Forum. 2021, 40(2): 425-433.
Lu A, Morris C J, Ebert D S, et al. Non-photorealistic volume rendering using stippling techniques[C]//IEEE Visualization, 2002. VIS 2002. IEEE, 2002: 211-218.
Schulz C, Kwan K C, Becher M, et al. Multi-class inverted stippling[J]. ACM Transactions on Graphics, 2021, 40(6).
Zhao J, Cao N, Wen Z, et al. # FluxFlow: Visual analysis of anomalous information spreading on social media[J]. IEEE transactions on visualization and computer graphics, 2014, 20(12): 1773-1782.
https://blog.csdn.net/pipisorry/article/details/53635895
https://blog.csdn.net/aliexken/article/details/106555993