几种基本数据结构--栈、队列、双向链表、有根树的分析和简单实现

    本文介绍几种基本数据结构--栈、队列、双向链表、有根树。

一、栈

    栈不用多说了，一种LIFO（后进先出）的数据结构，我们使用Java实现其入栈（PUSH），出栈（POP）的基本操作：

public class Stack {
    public final static int DEFAULTSIZE = 10;
    private final E[] elements;
    private int top;//下一次入栈的位置
    public Stack(){
        this(DEFAULTSIZE);
    }
    @SuppressWarnings("unchecked")
    public Stack(int size){
        elements = (E[]) new Object[size];
        top = 0;
    }
    
    public void push(E data){
        if(top >= elements.length)
            throw new IllegalArgumentException("Stack Overflow");
        elements[top++] = data;
    }
    
    public E pop(){
        if(top <= 0)
            throw new IllegalArgumentException("Stack Underflow");
        E data = elements[--top];
        elements[top] = null;//help GC
        return data;
    }
}

    栈是一种很简单也很基础的数据结构，但是这里使用Java实现的时候也要注意几点：

    1、注意栈的上溢出（overflow，也就是栈满了还进行push），以及栈的下溢出（underflow，也就是栈空还进行pop）的处理。

    2、首先为了保证每种栈可以存储不同数据类型我们使用了泛型，然后在创建盛装元素的数组的时候不能直接new一个泛型数组，因为泛型仅仅存在于编译期间，在运行期间会擦出，而内存分配是在运行期间做的，这矛盾了。因此不能直接new一个泛型数组，而是new一个Object数组，然后做一个强制类型转化，转化为对应泛型类型的数组。

    3、Java是一门有GC机制的语言，对于没有引用的堆对象会被GC回收。然而如果我们不需要再访问这个堆对象了，却一直保持着它的引用，这片内存就不会被回收。对于我们在pop的时候，我们就需要注意这点，如果我们只是return elements[top--]; 那么就会内存泄漏，因为我们弹出的元素内存仍然被elements数组维护着，而不会被GC。因此需要手动element[top] = null;  让应该被弹出的元素不再被引用。

二、队列

    队列也是一种很简单很基础的FIFO（先进先出）的数据结构，我们简单实现其入队（enqueue）和出队（dequeue）操作：

public class Queue {
    private int head;
    private int tail;//下次元素放的位置
    public static final int DEFAULT_SIZE = 10;
    private final E[] elements;
    @SuppressWarnings("unchecked")
    public Queue(int size){
        elements = (E[]) new Object[size+1];
        head = 0;
        tail = 0;
    }
    public Queue(){
        this(DEFAULT_SIZE);
    }
    public void enqueue(E x){
        if(head == tail+1)
            throw new IllegalArgumentException("Queue Overflow");
        elements[tail] = x;
        tail = (++tail)%elements.length;
    }
    public E dequeue(){
        if(head == tail)
            throw new IllegalArgumentException("Queue Underflow");
        E temp = elements[head];
        elements[head] = null;//help GC
        head = (++head)%elements.length;
        return temp;
    }
}

    同样，我们需要注意以下几点：

    1、我们使用size+1容量的数组来存储size容量队列，使用head表示队列头，tail表示队列尾。因为我们需要区分队列空和队列满，如果使用size容量来存储size容量队列就会发现队列满和队列空都是满足head = tail。然而使用size+1容量来存储的时候队列满时满足head = tail，此时如果继续enqueue就会queue overflow，队列空时满足head + 1 = tail，此时如果继续dequeue就会queue underflow。

    2、和栈一样，注意泛型的使用和GC问题，不要试图创建泛型数组，注意堆中不使用对象的引用清除。

三、双向链表

    链表是一种各对象按照线性顺序排列的数据结构，链表的顺序由个各对象里的后继指针next决定。而双向链表每个元素则有两个指针，一个前驱指针prev，一个后继指针next。下面是实现代码，实现双向链表的删除、插入、查找，我们使用了空头结点，这个头结点不包含数据，只是起到头的作用，也就是我们说的哨兵：

public class DoublyLinkedList {
    private static class LinkedNode{
        private E data;
        private LinkedNode prev;
        private LinkedNode next;
        public LinkedNode(E data){
            this.data = data;
        }
        public LinkedNode(){
            this.data = null;//头结点
        }
    }
    //空的头指针
    private LinkedNode head;
    public DoublyLinkedList(){
        head = new LinkedNode();
    }
    //将元素x插入到索引index的位置
    //插入到index应该找到index位置的前一个结点
    public void insert(int index, E x){
        //从头结点的第一个结点计数
        LinkedNode node = head;
        int i = 0;
        for( i = 0; i newNode = new LinkedNode(x);
        LinkedNode oldTail = node.next;
        node.next = newNode;
        if(oldTail != null){
            newNode.next = oldTail;
            oldTail.prev = newNode;
        }
        newNode.prev = node;
    }
    public LinkedNode search(E x){
        LinkedNode node = head.next;
        while( node!=null && node.data!=x ){
            node = node.next;
        }
        return node;
    }
    public boolean delete(E x){
        LinkedNode node = search(x);
        if(node==null)
            return false;
        else{
            //node为头结点的下一个结点
            if(node.prev!=head)
                node.prev.next = node.next;
            else
                head.next = node.next;
            if(node.next!=null)
                node.next.prev = node.prev;
            return true;
        }
    }
}

    链表作为一种很基础的数据结构没什么可说的，但是涉及到大量的指针操作，请注意边界判断，注意代码的鲁棒性。

四、有根树

    有根树就是一个相对比较复杂的基础数据结构了，有根树有一个根结点，根节点可能会存在子结点，子结点又可能会存在其他子结点，但是这些结点之间不可能构成图。

    我们首先讨论一下树的一些常用的表示方法。

    1、k孩子表示法

    显而易见的，我们会想到对于一个结点有子结点，我们就可以使用child1,child2,...,childk来表示k个子结点。但是这种方法会存在一个问题，就是我们有时候不确定要分配多少个属性来表示孩子。如果我们不使用属性，而是使用数组来表示孩子们，也会存在一个问题，就是我们不确定结点的孩子个数，所以我们总是需要开辟最大可能的数组，这就导致了空间的大量浪费。我们使用最简单的二叉树来实现这种表示方法：

public class BinaryTreeWithChildRep {
    private TreeNode root;
    public static class TreeNode{
        private E data;
        private TreeNode leftChild;
        private TreeNode rightChild;
        public TreeNode(E data){
            this.data = data;
        }
        public TreeNode(TreeNode leftChild, E data, TreeNode rightChild){
            this.data = data;
            this.leftChild = leftChild;
            this.rightChild = rightChild;
        }
    }
    public BinaryTreeWithChildRep(TreeNode root){
        this.root = root;
    }
    public static void main(String[] args) {
        TreeNode node4 = new TreeNode(4);
        TreeNode node5 = new TreeNode(5);
        TreeNode node2 = new TreeNode(node4, 3, node5);
        TreeNode node3 = new TreeNode(3);
        TreeNode node1 = new TreeNode(node2,1,node3);
        BinaryTreeWithChildRep tree = new BinaryTreeWithChildRep<>(node1);
    }
}

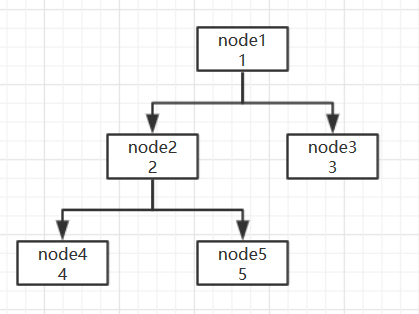
    对于上面的代码，我们就创建了这样一个二叉树：

    2、左孩子右兄弟表示法

    对于上面k孩子表示法中出现的问题，我们可以用左孩子右兄弟表示法来解决。对于树的每个结点只存在两个指针，一个leftChild表示最左边的孩子，一个rightSibling表示该结点右侧的兄弟结点。我们使用最简单的二叉树来实现这个表示方法：

public class BinaryTreeWithSiblingRep {
    public static class TreeNode {
        private E data;
        private TreeNode leftChild;
        private TreeNode rightSibling;
        public TreeNode(E data, TreeNode leftChild, TreeNode rightSibling){
            this.leftChild = leftChild;
            this.data = data;
            this.rightSibling = rightSibling;
        }
    }
    private TreeNode root;
    public BinaryTreeWithSiblingRep( TreeNode root) {
        this.root = root;
    }
    public static void main(String[] args) {
        TreeNode node5 = new TreeNode(5,null,null);
        TreeNode node4 = new TreeNode(4,null,node5);
        TreeNode node3 = new TreeNode(3,null,null);
        TreeNode node2 = new TreeNode(2,node4,node3);
        TreeNode node1 = new TreeNode(1,node2,node3);
        BinaryTreeWithSiblingRep tree = new BinaryTreeWithSiblingRep(node1); 
    }
}

    对于这段代码，我们创建的二叉树表示如下：

    3、数组表示法

    一棵n层高的树（根算第一层）总共最多可以有2^n-1个结点，因此对于一个n层高的树我们可以开辟一个2^n-1，其中第2^(i-1)-1到2^i个元素（从0开始计数）为第i层的元素对应序列。对于第i个结点（从0开始计数），如果有的话，其左结点为第2i+1个元素，右结点为2(i+1)个元素。这种表示方法很简单，而且访问某个元素的复杂度为O(1)，但是存在大量空间浪费。我们来实现一下二叉树中这种表示方式的左右子结点和父结点的获取：

public class BinaryTreeWithArrayRep {
    private final E[] elements;
    
    @SuppressWarnings("unchecked")
    public BinaryTreeWithArrayRep(E[] array){
        if(Integer.toBinaryString(array.length+1).lastIndexOf('1')!=0)
            throw new IllegalArgumentException("The length - 1 of the array is not the power of 2");
        elements = (E[]) new Object[array.length];
        System.arraycopy(array, 0, elements, 0, array.length);
    }
    public E getLeftChild(int index){
        int result = (index<<1)+1;
        if(result>1)-1>=0)
            return elements[(index>>1)-1];
        else if(index%2!=0&&index-1>>1>=0)
            return elements[index-1>>1];
        else
            return null;
    }
}

    可以看到这种表示方法十分简单，效率也很高。这里有一个小细节，我们构造参数传入数组的时候需要判断这个数组是不是2的整数次幂减一，我们可以把数组长度加一，转换成二进制，然后判断最后一个一的位置，以此来判断是不是2的整数次幂。

    当树的结点密度比较大或者没有对空间上的要求的时候就比较合适采用这种方法，否则这种方法会产生大量的空间浪费。

    以上树的三种表示方法只是常用的三种表示方法，每种方法都有其优点，具体用哪一种看具体需要。

    这就是本文介绍的所有的基本数据结构，如果有错误欢迎提出。