Python异常值检测——案例分析

目录

1.单个变量异常值检测

2. 双变量关系中的异常值检测

3. 使用线性回归来确定具有重大影响的数据点

4. 使用k最近邻算法找到离群值

5. 使用隔离森林算法查找异常

---

1.单个变量异常值检测

        如果某个值离平均值有多个标准偏差，并且远离近似标准正态分布的值，则我们更倾向于将将其视为异常值。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
import scipy.stats as scistat
data=pd.read_csv("F:\\python数据清洗\\04第四章\\covidtotals.csv")

data.columns

Index(['iso_code', 'lastdate', 'location', 'total_cases', 'total_deaths',
       'total_cases_pm', 'total_deaths_pm', 'population', 'pop_density',
       'median_age', 'gdp_per_capita', 'hosp_beds'],
      dtype='object')

data.set_index('iso_code',inplace=True)
totvars=['location', 'total_cases', 'total_deaths', 'total_cases_pm', 'total_deaths_pm']
demovars=['population', 'pop_density', 'median_age', 'gdp_per_capita', 'hosp_beds']

1.1 描述性统计 

data_b=data.loc[:,totvars]
data_b.describe()

	total_cases	total_deaths	total_cases_pm	total_deaths_pm
count	2.100000e+02	210.000000	210.000000	210.000000
mean	2.921614e+04	1770.714286	1355.357943	55.659129
std	1.363978e+05	8705.565857	2625.277497	144.785816
min	0.000000e+00	0.000000	0.000000	0.000000
25%	1.757500e+02	4.000000	92.541500	0.884750
50%	1.242500e+03	25.500000	280.928500	6.154000
75%	1.011700e+04	241.250000	1801.394750	31.777250
max	1.790191e+06	104383.000000	19771.348000	1237.551000

1.2 显示百分位数数据

data_b.quantile(np.arange(0.0,1.1,0.1))

	total_cases	total_deaths	total_cases_pm	total_deaths_pm
0.0	0.0	0.0	0.0000	0.0000
0.1	22.9	0.0	17.9986	0.0000
0.2	105.2	2.0	56.2910	0.3752
0.3	302.0	6.7	115.4341	1.7183
0.4	762.0	12.0	213.9734	3.9566
0.5	1242.5	25.5	280.9285	6.1540
0.6	2514.6	54.6	543.9562	12.2452
0.7	6959.8	137.2	1071.2442	25.9459
0.8	16847.2	323.2	2206.2982	49.9658
0.9	46513.1	1616.9	3765.1363	138.9045
1.0	1790191.0	104383.0	19771.3480	1237.5510

1.3 偏度(skewness)&峰度(kurtosis) 

        偏度和峰度分别描述了分布的对称性和分布的尾部有多肥。如果变量以正态分布，则这两个指标都大大高于预期。

# 偏度skewness
data_b.skew()
----------------------------
total_cases        10.804275
total_deaths        8.929816
total_cases_pm      4.396091
total_deaths_pm     4.674417
dtype: float64


# 峰度kurtosis
data_b.kurtosis()
----------------------------
total_cases        134.979577
total_deaths        95.737841
total_cases_pm      25.242790
total_deaths_pm     27.238232
dtype: float64

1.4 测试数据的正态分布性

        使用scipy库中的Shapiro-Wilk测试，输出测试的p值。正态分布的null假设可以在低于0.05的任何p值和95%的置信水平上被拒绝。

def testnorm(var,df):
    stat,p=scistat.shapiro(df[var])
    return p

testnorm("total_cases",data_b) #3.753789128593843e-29
testnorm("total_deaths",data_b) #4.3427896631016077e-29
testnorm("total_cases_pm",data_b) #1.3972683006509067e-23
testnorm("total_deaths_pm",data_b) #1.361060423265974e-25

结果表明变量的分布在高显著水平下不是正态的。

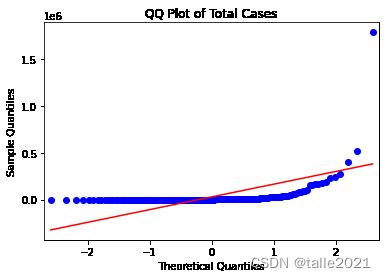
# 总病例数的分位数图（qq图）,直线显示的是正态分布应有的外观
sm.qqplot(data_b[["total_cases"]].sort_values(['total_cases']),line='s')
plt.title('QQ Plot of Total Cases')
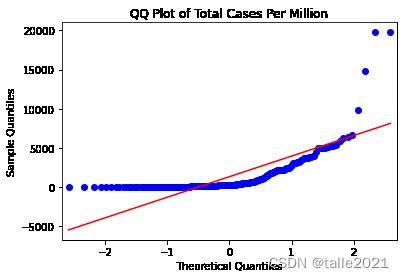
plt.show()

# 每百万人口的总病例数的分位数图（qq图）
sm.qqplot(data_b[["total_cases_pm"]].sort_values(['total_cases_pm']),line='s')
plt.title('QQ Plot of Total Cases Per Million')
plt.show()

 

qqplot的结果也表明，total_cases(总病例数)和total_cases_pm(每百万人口的总病例数)的分布都与正态分布有显著差异(红色直线显示的是正态分布应有的外观)

1.5 显示离群值范围

        定义变量离群值的一种方法是按四分位数的距离计算。第三个四分位数(0.75)被称为上四分位数，第一个四分位数(0.25)被称为下四分位数，上四分位数和下四分位数之间的距离称为四分位距，也就是0.25~0.75分位数的范围。如果某个值离均值大于1.5倍，则认为该值是离群值。

def getoutliers():
    dfout=pd.DataFrame(columns=data.columns,data=None)
    for col in data_b.columns[1:]:
        thirdq,firstq=data_b[col].quantile(0.75),data_b[col].quantile(0.25) #计算四分位数
        range_q=1.5*(thirdq-firstq) #四分位距
        high,low=range_q+thirdq,firstq-range_q #离群阈值
        df=data.loc[(data[col]>high) | (data[col]

	lastdate	location	total_cases	total_deaths	total_cases_pm	total_deaths_pm	population	pop_density	median_age	gdp_per_capita	hosp_beds	varname	threshlow	threshhigh
BGD	2020-06-01	Bangladesh	47153	650	286.315	3.947	164689383.0	1265.036	27.5	3523.984	0.80	total_cases	-14736.125	25028.875
BLR	2020-06-01	Belarus	42556	235	4503.604	24.870	9449321.0	46.858	40.3	17167.967	11.00	total_cases	-14736.125	25028.875
BEL	2020-06-01	Belgium	58381	9467	5037.354	816.852	11589616.0	375.564	41.8	42658.576	5.64	total_cases	-14736.125	25028.875
BRA	2020-06-01	Brazil	514849	29314	2422.142	137.910	212559409.0	25.040	33.5	14103.452	2.20	total_cases	-14736.125	25028.875
CAN	2020-06-01	Canada	90936	7295	2409.401	193.285	37742157.0	4.037	41.4	44017.591	2.50	total_cases	-14736.125	25028.875
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
ESP	2020-05-31	Spain	239429	27127	5120.952	580.197	46754783.0	93.105	45.5	34272.360	2.97	total_deaths_pm	-45.454	78.116
SWE	2020-06-01	Sweden	37542	4395	3717.298	435.180	10099270.0	24.718	41.0	46949.283	2.22	total_deaths_pm	-45.454	78.116
CHE	2020-06-01	Switzerland	30779	1656	3556.367	191.343	8654618.0	214.243	43.1	57410.166	4.53	total_deaths_pm	-45.454	78.116
GBR	2020-06-01	United Kingdom	274762	38489	4047.403	566.965	67886004.0	272.898	40.8	39753.244	2.54	total_deaths_pm	-45.454	78.116
USA	2020-06-01	United States	1790191	104383	5408.389	315.354	331002647.0	35.608	38.3	54225.446	2.77	total_deaths_pm	-45.454	78.116

outliers.varname.value_counts()

total_deaths       36
total_cases        33
total_deaths_pm    28
total_cases_pm     17
Name: varname, dtype: int64

2. 双变量关系中的异常值检测

        当某个值的分布与平均值没有明显偏离时，即使它不是极值，它也可能是异常值。当第二个变量具有某些值时，第一个变量的某些值就可能是异常值。（以下使用的还是之前的数据）

2.1 生成相关性矩阵

data.corr(method="pearson")

	total_cases	total_deaths	total_cases_pm	total_deaths_pm	population	pop_density	median_age	gdp_per_capita	hosp_beds
total_cases	1.000000	0.932079	0.182246	0.247464	0.270030	-0.028737	0.162698	0.186835	0.027601
total_deaths	0.932079	1.000000	0.179812	0.394811	0.212619	-0.031645	0.205128	0.198729	0.019990
total_cases_pm	0.182246	0.179812	1.000000	0.586468	-0.056009	0.110043	0.313836	0.651200	0.081449
total_deaths_pm	0.247464	0.394811	0.586468	1.000000	-0.013902	0.030281	0.389595	0.383672	0.120488
population	0.270030	0.212619	-0.056009	-0.013902	1.000000	-0.023084	0.024395	-0.059555	-0.038329
pop_density	-0.028737	-0.031645	0.110043	0.030281	-0.023084	1.000000	0.178878	0.315199	0.314973
median_age	0.162698	0.205128	0.313836	0.389595	0.024395	0.178878	1.000000	0.648905	0.662222
gdp_per_capita	0.186835	0.198729	0.651200	0.383672	-0.059555	0.315199	0.648905	1.000000	0.296995
hosp_beds	0.027601	0.019990	0.081449	0.120488	-0.038329	0.314973	0.662222	0.296995	1.000000

从上表可看出，总病例数与总死亡数之间的相关性非常高(0.93)，而每百万人口总病例数与每百万人口总死亡数之间的相关性则较小(0.59)，人均GDP与每百万人口总病例数之间也存在较强的相关关系(0.65)。

2.2 创建不同变量分位数的交叉表

        首先创建一个DataFrame，使用qcut创建一个将数据分解为分位数的列，显示总病例数分位数与总死亡数数分位数的交叉表。

data_b['total_cases_q']=pd.qcut(data_b['total_cases'],labels=['very low','low','medium','high','very high'],q=5,precision=0)
data_b['total_deaths_q']=pd.qcut(data_b['total_deaths'],labels=['very low','low','medium','high','very high'],q=5,precision=0)
pd.crosstab(data_b.total_cases_q,data_b.total_deaths_q)

total_deaths_q	very low	low	medium	high	very high
total_cases_q
very low	34	7	1	0	0
low	12	19	10	1	0
medium	1	13	15	13	0
high	0	0	12	24	6
very high	0	0	2	4	36

data.loc[(data_b.total_cases_q=="very high")&(data_b.total_deaths_q=="medium")].T

iso_code	QAT	SGP
lastdate	2020-06-01	2020-06-01
location	Qatar	Singapore
total_cases	56910	34884
total_deaths	38	23
total_cases_pm	19753.146	5962.727
total_deaths_pm	13.19	3.931
population	2881060.0	5850343.0
pop_density	227.322	7915.731
median_age	31.9	42.4
gdp_per_capita	116935.6	85535.383
hosp_beds	1.2	2.4

从表中可以看出，大多数国家都在对角线上或其附近，但有2个国家(卡塔尔，新加坡)的病例数很高，但死亡人数时中等的。

2.3 绘制两个变量间的散点图

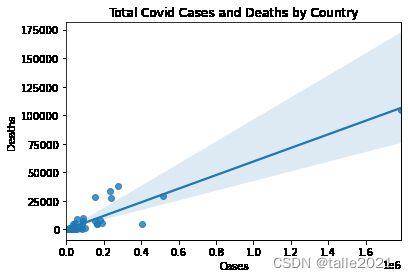
        使用seaborn的regplot方法时，除生成散点图外，还可以生成线性回归线。

import seaborn as sns
ax=sns.regplot(x="total_cases",y="total_deaths",data=data)
ax.set(xlabel='Cases',ylabel='Deaths',title='Total Covid Cases and Deaths by Country')
plt.show()

# 检查回归线上方的意外值
data.loc[(data.total_cases<300000) & (data.total_deaths>20000)].T

iso_code	FRA	ITA	ESP	GBR
lastdate	2020-06-01	2020-06-01	2020-05-31	2020-06-01
location	France	Italy	Spain	United Kingdom
total_cases	151753	233019	239429	274762
total_deaths	28802	33415	27127	38489
total_cases_pm	2324.879	3853.985	5120.952	4047.403
total_deaths_pm	441.251	552.663	580.197	566.965
population	65273512.0	60461828.0	46754783.0	67886004.0
pop_density	122.578	205.859	93.105	272.898
median_age	42.0	47.9	45.5	40.8
gdp_per_capita	38605.671	35220.084	34272.36	39753.244
hosp_beds	5.98	3.18	2.97	2.54

# 检查回归线下方的意外值
data.loc[(data.total_cases>400000) & (data.total_deaths<10000)].T

iso_code	RUS
lastdate	2020-06-01
location	Russia
total_cases	405843
total_deaths	4693
total_cases_pm	2780.995
total_deaths_pm	32.158
population	145934460.0
pop_density	8.823
median_age	39.6
gdp_per_capita	24765.954
hosp_beds	8.05

从上表结果来看，有4个国家(法国，意大利，西班牙和英国)的病例数少于30w，死亡人数却超过2w；有1个国家(俄罗斯)的病例数超过30w，但死亡人数少于1w。

3. 使用线性回归来确定具有重大影响的数据点

        使用线性回归的优势在于他们对于变量的分布依赖性较小，并且能比单变量或双变量分析揭示更多的东西，识别出在其它方面不显著的异常值。

        使用statsmodels OLS方法拟合每百万人口总病例数的线性回归模型，然后确定那些对该模型具有较大影响的国家/地区。

3.1 描述性统计

xvars=['pop_density','median_age','gdp_per_capita']
data_x=data.loc[:,['total_cases_pm']+xvars].dropna()
data_x.describe()

	total_cases_pm	pop_density	median_age	gdp_per_capita
count	175.000000	175.000000	175.000000	175.000000
mean	1134.015709	247.151863	30.537143	19008.385423
std	2101.363772	822.398967	9.117751	19673.386571
min	0.000000	1.980000	15.100000	661.240000
25%	67.448000	36.066000	22.300000	4458.202500
50%	263.413000	82.328000	29.700000	12951.839000
75%	1357.506000	207.960000	38.700000	27467.146000
max	19753.146000	7915.731000	48.200000	116935.600000

3.2 拟合线性回归模型 

def getlm(df):
    Y=df.total_cases_pm
    X=df[['pop_density','median_age','gdp_per_capita']]
    X=sm.add_constant(X)
    return sm.OLS(Y,X).fit()

lm=getlm(data_x)
lm.summary()

	coef	std err	t	P>|t|	[0.025	0.975]
const	944.4731	426.712	2.213	0.028	102.172	1786.774
pop_density	-0.2057	0.142	-1.447	0.150	-0.486	0.075
median_age	-49.4398	16.013	-3.088	0.002	-81.048	-17.832
gdp_per_capita	0.0921	0.008	12.015	0.000	0.077	0.107

3.3 确定对模型影响较大的国家/地区，并绘制影响图

        在线性回归中，库克距离描述了单个样本对整个回归模型的影响程度，库克距离越大，说明影响越大。当库克距离大于0.5应仔细检查。

influence=lm.get_influence().summary_frame()
influence.loc[influence.cooks_d>0.5,['cooks_d']]

iso_code	cooks_d
		HKG	0.780662
QAT	5.080180

data_x.loc[influence.cooks_d>0.5]

	total_cases_pm	pop_density	median_age	gdp_per_capita
iso_code
HKG	0.000	7039.714	44.8	56054.92
QAT	19753.146	227.322	31.9	116935.60

fig,ax=plt.subplots(figsize=(12,8))
sm.graphics.influence_plot(lm,ax=ax,criterion="cooks")
plt.show()

3.4 删除离群点，再进行回归拟合

data_x_new=data_x.loc[influence.cooks_d<0.5]
lm=getlm(data_x_new)
lm.summary()

	coef	std err	t	P>|t|	[0.025	0.975]
const	44.0854	349.924	0.126	0.900	-646.700	734.870
pop_density	0.2423	0.145	1.666	0.098	-0.045	0.529
median_age	-2.5165	13.526	-0.186	0.853	-29.217	24.184
gdp_per_capita	0.0557	0.007	7.875	0.000	0.042	0.070

删除之后，常数和median_age的估计值不再有效。回归输出的P>|t|值表明该系数是否与0有着显著不同。在第一次回归中，median_age和gdp_per_capita的系数在99%的置信水平上是显著的；即P>|t|小于0.01。而在删除两个离群值的情况下，只有gdp_per_capita是显著的。因此在处理此问题时，应分析诸如此类的离群值是否会增加重要信息或使模型失真。

4. 使用k最近邻算法找到离群值

        在使用线性回归中，我们使用了每百万人口病例数作为因变量，而在没有标签数据的情况下，即没有目标变量或因变量时，无监督的机器学习工具也可以识别与其它观察结果不同的观察结果。

from pyod.models.knn import KNN
from sklearn.preprocessing import StandardScaler
# 创建分析列的标准化DataFrame
standardizer=StandardScaler()
var1=['location','total_cases_pm', 'total_deaths_pm', 'pop_density','median_age', 'gdp_per_capita']
data_var1=data.loc[:,var1].dropna()
data_var1_stand=standardizer.fit_transform(data_var1.iloc[:,1:])
# KNN模型生成异常分数
clf_name='KNN'
clf=KNN(contamination=0.1) #contamination:异常样本的百分比，在[0,0.5]之间的float型，默认为0.5
clf.fit(data_var1_stand)
y_pred=clf.labels_ # 返回训练数据上的分类标签 (0: 正常值, 1: 异常值)
y_scores=clf.decision_scores_  # 返回训练数据上的异常值 (分值越大越异常)
pred=pd.DataFrame(zip(y_pred,y_scores),columns=['outlier','scores'],index=data_var1.index)

pred.outlier.value_counts()

0    157
1     18
Name: outlier, dtype: int64

显示离群的数据

data_var1.join(pred).loc[pred.outlier==1,['location','total_cases_pm','total_deaths_pm','scores']].sort_values(['scores'],ascending=False)

	location	total_cases_pm	total_deaths_pm	scores
iso_code
SGP	Singapore	5962.727	3.931	9.228543
HKG	Hong Kong	0.000	0.000	7.770444
QAT	Qatar	19753.146	13.190	2.643709
BHR	Bahrain	6698.468	11.166	2.049642
LUX	Luxembourg	6418.776	175.726	1.525783
MDV	Maldives	3280.041	9.250	1.395496
MLT	Malta	1395.120	15.854	1.353541
BGD	Bangladesh	286.315	3.947	1.117904
BRN	Brunei	322.298	4.572	1.108011
SAU	Saudi Arabia	2449.053	14.448	0.902926
ARE	United Arab Emirates	3493.994	26.693	0.822334
KWT	Kuwait	6332.420	49.642	0.803449
BRB	Barbados	320.144	24.359	0.740434
IRL	Ireland	5060.962	334.562	0.721934
PSE	Palestine	122.907	0.980	0.717875
NOR	Norway	1551.489	43.532	0.712298
GNQ	Equatorial Guinea	930.872	8.553	0.695340
OMN	Oman	2239.641	9.204	0.670568

从上表可以看出，新加坡、卡塔尔的决策分数显著高于其它国家/地区，与前面的分析结果一致。

5. 使用隔离森林算法查找异常

        隔离森林（isolation forest，也称孤立森林）找到离群点的方法是，对数据进行连续分区，直至某个数据点被隔离。如果某个数据点仅需要很少的分区即可隔离，那么它将获得较高的异常分数。

from sklearn.ensemble import IsolationForest
from mpl_toolkits.mplot3d import Axes3D
var2=['location','total_cases_pm', 'total_deaths_pm', 'pop_density','median_age', 'gdp_per_capita']
standardizer=StandardScaler()
data_var2=data.loc[:,var2].dropna()
data_var2_stand=standardizer.fit_transform(data_var2.iloc[:,1:])
clf=IsolationForest(n_estimators=100,max_samples='auto',contamination=0.1,max_features=1.0)
clf.fit(data_var2_stand)
data_var2['anomaly']=clf.predict(data_var2_stand) #查看隔离森林得出的结果，输出为一维矩阵，其中值为1代表为正常数据点，值为-1代表为异常点
data_var2['scores']=clf.decision_function(data_var2_stand)  #数据集中样本的异常分数值，注意其中值是以0为阈值，小于0视为异常，大于0视为正常，

data_var2.anomaly.value_counts()

 1    157
-1     18
Name: anomaly, dtype: int64

# 创建离群值和内围值的DataFrame
inlier,outlier=data_var2.loc[data_var2.anomaly==1],data_var2.loc[data_var2.anomaly==-1]
outlier[['location','total_cases_pm','total_deaths_pm','anomaly','scores']].sort_values(['scores']).head(10)

	location	total_cases_pm	total_deaths_pm	anomaly	scores
iso_code
QAT	Qatar	19753.146	13.190	-1	-0.257773
SGP	Singapore	5962.727	3.931	-1	-0.199578
HKG	Hong Kong	0.000	0.000	-1	-0.166863
BEL	Belgium	5037.354	816.852	-1	-0.116571
BHR	Bahrain	6698.468	11.166	-1	-0.110567
LUX	Luxembourg	6418.776	175.726	-1	-0.097430
ITA	Italy	3853.985	552.663	-1	-0.066504
ESP	Spain	5120.952	580.197	-1	-0.060739
IRL	Ireland	5060.962	334.562	-1	-0.040109
MDV	Maldives	3280.041	9.250	-1	-0.031414

ax=plt.axes(projection='3d')
ax.set_title('Isolation Forest Anomaly Detection')
ax.set_zlabel("Cases Per Million")
ax.set_xlabel("GDP Per Capita")
ax.set_ylabel("Median Age")
ax.scatter3D(inlier.gdp_per_capita,inlier.median_age,inlier.total_cases_pm,label="inlier",c='blue')
ax.scatter3D(outlier.gdp_per_capita,outlier.median_age,outlier.total_cases_pm,label="outlier",c='red')
ax.legend()
plt.tight_layout()
plt.show()

 隔离森林的结果与k最近邻的结果非常相似，卡塔尔、新加坡的异常得分较高（准确地说是最小负分），因此，当进行多变量分析时，可以考虑删除离群值再进行分析。