卡尔曼滤波（三）（最优化递归数字处理算法）

卡尔曼增益的推导

（0）视频推荐和前言

---

​​​​​​【卡尔曼滤波器】3_卡尔曼增益超详细数学推导 ～全网最完整_哔哩哔哩_bilibili

---

协方差矩阵都是对称矩阵，求逆也是对称矩阵，并且它很可能是对角阵，也就是除了对角线以外其

他元素都是0，因为不同的状态变量收到的干扰之间一般不会有所联系，所以它们的协方差为0；噪

声和误差符合正态分布，并且可以用它们的协方差矩阵来近似的量化它们，它们的协方差矩阵又比

较特殊，用P表示它们的协方差，用X代表噪声或者误差本身，则P = E【X * X的转置】

---

下面会涉及到以下的协方差矩阵：

过程噪音W的协方差矩阵Q

测量噪音V的协方差矩阵R

先验误差E（k）的协方差矩阵P【E（k）】

后验误差E_New（k）的协方差矩阵P_New【E_New（k）】

（1）引入不确定性的状态空间方程表达

---

引入过程噪音，计算得到的状态变量：X（k）= A2 *  X（k-1）+ B2 * U（k）+ W（k-1）

引入测量噪音后，测量得到的状态变量：Z（k）= H * X（k）+ V（k）

我们的目的：去补偿缺失的W（k-1），去削弱测量得到的状态变量包含的 V（k）

---

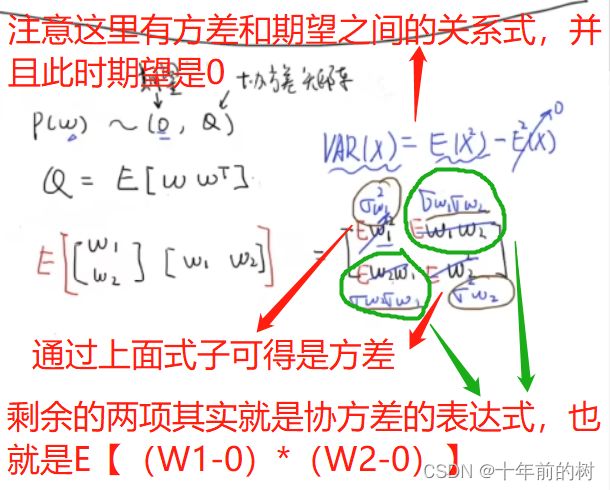
过程噪音和测量噪音无法通过建模得到，但是它们符合正态分布，也就是P（W）~（0，Q）、P

（V）~（0，R），其中Q和R矩阵是协方差矩阵，并且Q = E【 W * W的转置 】、R = E【 V * V的

转置 】，此时的协方差矩阵的公式，推导如下：

 （2）不包含不确定性的状态空间方程表达

---

由于不确定性（这里说的是噪声所产生的那部分影响）是无法得到的，所以状态空间方程先去掉不

确定性，这个时候测量得到的不包含不确定性的值反而是我们想要的，结果如下：

计算得到的状态变量：X（k）= A2 * X（k-1）+ B2 * U（k）

测量得到的状态变量：Z（k）= H * X（k）

---

由于去掉了不确定性，所以第一个式子和第二个式子得到的算是估计值，做一下符号改动： 

X_Hat（k）= A2 * X_Hat_New（k-1）+ B2 * U（k），X_Hat是计算得到的这一时刻的估计值，称

作先验估计值。在这里涉及到了后验估计值，它算是每一次估计周期得到的最后的估计结果

X_Hat_Meas（k）= H矩阵的逆 * Z（k），X_Hat_Meas是测量得到的这一时刻的估计值，剔除了

测量噪声所带来的影响，其中H矩阵其实是单位对角阵

（3）卡尔曼滤波使用

---

应该注意：现实当中的传感器测量到的值，都是带有噪声产生的那部分影响，也包含传感器测量误

差带来的那部分影响

---

通过卡尔曼滤波和上面的两个估计值，使用数据融合去得到一个准确的值

后验估计值：X_Hat_New（k) = X_Hat（k) + G *【 X_Hat_Meas（k） - X_Hat（k）】，其中

G = K（k）* H，而上面这个表达式里面，X_Hat_Meas（k）里面有H矩阵的逆，可将G的表达式

和X_Hat_Meas（k）的表达式代入，得到数据融合后的一个表达式：

X_Hat_New（k) = X_Hat（k) + K（k）*【Z（k) - H * X_Hat（k）】

此时的目标，便是寻找K（k）使得X_Hat_New（k)接近实际值X（k），也就是使得误差最小。这 

里的X（k）是引入了不确定性后的状态空间方程中的X（k），也就是补偿了由于模型不够准确而

缺失的那部分影响

---

引入先验误差E（k）= X（k）-X_Hat（k) 和 后验误差E_New（k）= X（k）- X_Hat_New（k)，

其中 E（k）和 E_New（k）都符合正态分布，先讨论后验误差，即P【E_New（k）】~

（0,P_New），其中P_New是后验误差的协方差矩阵，P_New = E 【 E_New（k）* E_New（k）

的转置】，特殊的是：P_New矩阵的对角线其实是各个维度的状态变量的误差的方差，只要满足

P_New矩阵的迹（矩阵的迹＝对角线相加，此时刚好是各个维度的状态变量的误差的方差之和）

最小，即可得出最优解

---

具体的推导过程这里不做详细解释，下面只描述一下推导过程，这里会涉及到矩阵转置的性质、期

望的性质、矩阵的迹、矩阵的求导。

这个时候就可以先去求解P_New矩阵的表达式（E_New（k）的表达式已知），然后去求这个

P_New矩阵的迹，迹显然是关于K（k）的一个表达式，然后这个表达式对K（k）求导并令它为0，

从而找到K（k）的最终表达式

---

卡尔曼增益系数：K（k） = （ H * P【E（k）】* H的转置 + R ）的逆 * P【E（k）】* H的转置

H矩阵是观测矩阵，是在测量得到的状态变量的表达式中出现的

P【E（k）】是先验误差的协方差矩阵

R矩阵是测量噪音的协方差矩阵

如果测量噪音带来的影响很大，也就是R矩阵会很大地影响卡尔曼增益系数的计算，那么可以发现

此时卡尔曼增益系数接近于0，就会使得数据融合后的表达式所得到的后验估计值更多地接近于先

验估计值，也就是愿意去相信计算得到的结果；反之，测量噪音基本没有影响的时候，后验估计值

更多地接近于测量估计值，也就是愿意去相信测量得到的结果