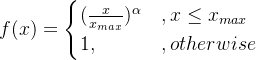GloVe之Pytorch实现_代码部分
1.数据预处理
使用的是一份英文数据集。其网盘地址如下：
实现工具：Jupyter
链接：https://pan.baidu.com/s/1eAX_t9GrkANFKcT34NteZw
提取码：7m14
这里简单做一些数据分词、建立索引表、统计词频的一些简单工作，这些工作在后面的共现矩阵以及权重矩阵计算都有用到：
from collections import Counterwith open("train.txt","r",encoding="utf-8") as f:
corpus=f.read()
corpus=corpus.lower().split(" ")
#设置词典大小
vocab_size=10000
#统计词的数量，原数据约24万个单词,这里获取前1万个（笔记本存不了所有）
word_count=dict(Counter(corpus).most_common(vocab_size-1))
#表示为登陆词（新词）
word_count[""]=len(corpus)-sum(list(word_count.values()))
#建立词表索引
idx2word=list(word_count.keys())
word2idx={w:i for i,w in enumerate(idx2word)} 2.建立共现矩阵
为什么要建立共现矩阵？上节推导的损失函数为：
其中
表示共现次数，也可以看做是Glove训练的一个标签（Glove是无监督的算法）。因此必须要有一个存储他们的共现频数的地方，即共现矩阵。关于共现矩阵的建立方法其实也比较精妙，我们在讨论表示的是词k出现在词i的关联窗口中，但是我们在编码的时候总不能行列索引根据词吧（pandas可以实现），这里有一个精妙的转化就是，之前我们建立的词索引，即假设“a”的索引为0，“b”的索引为1，那么我们建立的矩阵中
表示的是以a为中心词的窗口中b出现的次数，要知道我们是有word2idx和idx2word来找到这种映射联系。
import numpy as np
import syswindow_size=5coMatrix=np.zeros((vocab_size,vocab_size),np.int32)
print("共现矩阵占内存大小为：{}MB".format(sys.getsizeof(coMatrix)/(1024*1024)))
#语料库进行编码
corpus_encode=[word2idx.get(w,1999) for w in corpus]
#遍历语料库
for i,center_word in enumerate(corpus_encode):
#这一步和word2vec一样，提取背景词，但是后面有要防止边界越界
pos_indices=list(range(i-window_size,i))+list(range(i+1,i+1+window_size))
pos_indices=[idx%len(corpus_encode) for idx in pos_indices]
context_word=[corpus_encode[idx] for idx in pos_indices]
#context_word代表当前center_word周围的所有关联词
for word_idx in context_word:
coMatrix[center_word][word_idx]+=1
if((i+1)%1000000==0):
print("已完成{}/{}".format(i+1,len(corpus_encode)))由于共现矩阵很重要，我们必须要进行验证，我们知道共现矩阵是一个对称阵，因此我们从这方面去验证：
#统计出来的应该是对称矩阵
for i in range(vocab_size):
#遍历下三角即可
for j in range(i):
#若不相等，则说明有错
if(coMatrix[i][j]!=coMatrix[j][i]):
print("共现矩阵有误行{}列{}不等".format(i,j))没有任何输出，因此我们的共现矩阵是对的
我们有了共现矩阵以后，那么语料库我们将不在需要，因为语料库里面的信息都反应在共现矩阵上
del corpus,corpus_encode3.惩罚系数矩阵
继续观察损失函数
我们发现除了需要共现频数以外，还需要知道惩罚系数
，惩罚系数函数如下：
因此我们需要建立一个与共现矩阵一样大小的惩罚系数矩阵来存储惩罚系数，这里我们按照原文将（
，
）：
xMax=100
alpha=0.75wMatrix=np.zeros_like(coMatrix,np.float32)
print("惩罚系数矩阵矩阵占内存大小为：{}MB".format(sys.getsizeof(wMatrix)/(1024*1024)))
for i in range(vocab_size):
for j in range(vocab_size):
if(coMatrix[i][j]>0):
wMatrix[i][j]=(coMatrix[i][j]/xMax)**alpha if coMatrix[i][j]4.生成dataset数据集
观察损失函数:
我们希望生成的dataset数据集可以提供给我们某中心词
和背景词k（需要他们在模型的embedding中获取
）,以及他们的共现频次和惩罚系数：
import torch
from torch.utils.data.dataset import Dataset
from torch.utils.data.dataloader import DataLoaderbatch_size=10#这里有一个比较重要的地方,就是共现频次为0代入计算对模型没有帮助，为了提高效率
#我们仅仅收集共现频次不是0的中心词和背景词
#其次频次为0在计算log0的时候也可能引起错误
train_set=[]
for i in range(vocab_size):
for j in range(vocab_size):
if(coMatrix[i][j]!=0):
train_set.append([i,j])
if((i+1)%1000==0):
print("已完成{}/{}".format(i+1,vocab_size))class dataset(Dataset):
def __init__(self,coMatrix,wMatrix,train_set):
super(dataset,self).__init__()
self.coMatrix=torch.Tensor(coMatrix)
self.wMatrix=torch.Tensor(wMatrix)
self.train_set=torch.Tensor(train_set)
def __len__(self):
return len(self.train_set)
def __getitem__(self,idx):
#中心词和背景词
i,k=train_set[idx]
#共现频次
x_ik=self.coMatrix[i][k]
#惩罚系数
w=self.wMatrix[i][k]
return i,k,x_ik,w写一段测试代码：
data=dataset(coMatrix,wMatrix,train_set)
dataloader=DataLoader(data,batch_size,shuffle=True,drop_last=True,num_workers=0)for x,y,z,e in dataloader:
print(x.shape,y.shape,z.shape,e.shape)
break结果为：
torch.Size([10]) torch.Size([10]) torch.Size([10]) torch.Size([10])没有问题，因为我们已经做好了数据生成的构造器，此时我们就可以删除共现矩阵和惩罚系数矩阵（占地太大）：
del coMatrix,wMatrix5.创建模型
观察损失函数:
我们训练的参数有4个，分别是中心词和背景词向量以及其偏置：
import torch.nn as nn
from torch.nn.modules import Module class GloVe(Module):
def __init__(self,vocab_size,d_model=50):
super(GloVe,self).__init__()
self.vocab_size=vocab_size
self.d_model=d_model
#中心词矩阵和背景词矩阵
self.V=nn.Embedding(vocab_size,d_model)
self.U=nn.Embedding(vocab_size,d_model)
#中心词偏置和背景词偏置
self.B_v=nn.Embedding(vocab_size,1)
self.B_u=nn.Embedding(vocab_size,1)
#随机初始化参数(这种初始化方式收敛更快)，embedding原来是默认（0,1）正态分布
initrange = 0.5 / self.vocab_size
self.V.weight.data.uniform_(-initrange, initrange)
self.U.weight.data.uniform_(-initrange, initrange)
self.B_v.weight.data.uniform_(-initrange, initrange)
self.B_u.weight.data.uniform_(-initrange, initrange)
def forward(self,i,k,x_ik,w):#输入的是中心词，背景词，共现频数，惩罚系数
#i[batch],k[batch],x_ik[batch],f_x_ik[batch]
v_i=self.V(i)
u_k=self.U(k)
b_i=self.B_v(i)
b_k=self.B_u(k)
#v_i[batch,d_model] u_k[batch,d_model] b_i[batch,1] b_k[batch,1]
#这里要清楚torch.mul()是矩阵按位相乘，两个矩阵的shape要相同
#torch.mm()则是矩阵的乘法
loss=(torch.mul(v_i,u_k).sum(dim=1)+b_i+b_k-torch.log(x_ik))**2
#loss[batch]
loss=loss*w*0.5
return loss.sum()
def get_embeding(self):
#两者相加输出，而非取其中一个
return self.V.weight.data.cpu().numpy()+self.U.weight.data.cpu().numpy()我们测试一下模型写的是否有问题：
d_model=100
model=GloVe(vocab_size,d_model)
model(x,y,z,e)结果为：
tensor(25.9712, grad_fn=) 能正常输出。
6.训练
准备工作以及做完，接下来就是水到渠成的事情，这里我们的优化器选择Adam，同时为了观测训练效果，在迭代到一定次数的时候观察某一向量附近的词：
import scipy
from torch.optim.adagrad import Adagrad
#切记不是Adam，那个是反过来优化...
from sklearn.metrics.pairwise import cosine_similarity#寻找附近的词，和Word2vec一样
def nearest_word(word, embedding_weights):
index = word2idx[word]
embedding = embedding_weights[index]
cos_dis = np.array([scipy.spatial.distance.cosine(e, embedding) for e in embedding_weights],np.float)
return [idx2word[i] for i in cos_dis.argsort()[:10]]#找到前10个最相近词语for epoch in range(epochs):
allloss=0
for step,(i,k,x_ik,w) in enumerate(dataloader):
if(cuda):
i=i.cuda()
k=k.cuda()
x_ik=x_ik.cuda()
w=w.cuda()
#反向传播梯度更新
optim.zero_grad()
loss=model(i,k,x_ik,w)
loss.backward()
optim.step()
#记录总损失
allloss+=allloss
if((step+1)%2000==0):
print("epoch:{}, iter:{}, loss:{}".format(epoch+1,step+1,allloss/(step+1)))
if((step+1)%5000==0):
print("nearest to one is{}".format(nearest_word("one",model.get_embeding())))7.参考
自学阶段重点主要看了该博主的代码，然后自己重新复现。所以在我自己重新复现GloVe代码的时候，很多都与该博主的代码相似
一个基于PyTorch实现的Glove词向量的实例：https://blog.csdn.net/a553181867/article/details/104837957/