代码随想录算法训练营第22天 | 235. 二叉搜索树的最近公共祖先 701.二叉搜索树中的插入操作 450.删除二叉搜索树中的节点

代码随想录系列文章目录

二叉树篇-二叉搜索树

---

---

235. 二叉搜索树的最近公共祖先

题目链接

和二叉树的最近祖先那道题的差别

236.二叉树的最近公共祖先，利用回溯从底向上搜索，遇到一个节点的左子树里有p，右子树里有q，那么当前节点就是最近公共祖先。

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        if not root: return None
        if root == q or root == p: return root
        
        left = self.lowestCommonAncestor(root.left, p, q)      #左
        right = self.lowestCommonAncestor(root.right, p, q)    #右
                                                               #中
        if left != None and right != None:       
            return root                             #左子树 右子树 发现pq
        elif left == None and right != None:
            return right                            #返回有发现qp 那个子树，即不空的子树
        elif left != None and right == None:
            return left
        else: return None

本题是二叉搜索树，二叉搜索树是有序的，那得好好利用一下这个特点。
其实只要从上到下遍历的时候，cur节点是数值在[p, q]区间中则说明该节点cur就是最近公共祖先了。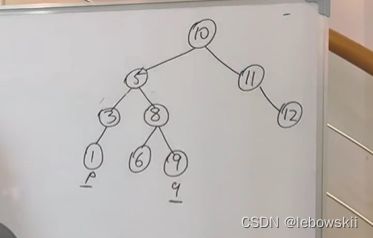
为什么呢？如图，此时 5 在 p 和 q的中间，如果往左子树走了，右边的q会被失掉，反之亦然

普通二叉树求最近公共祖先需要使用回溯，从底向上来查找，二叉搜索树就不用了，因为搜索树有序（相当于自带方向），那么只要从上向下遍历就可以了。

那么我们可以采用前序遍历（其实这里没有中节点的处理逻辑，遍历顺序无所谓了）。

可以看出直接按照指定的方向，就可以找到节点4，为最近公共祖先，而且不需要遍历整棵树，找到结果直接返回！

dfs

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        if not root: return None
        if p.val < root.val and q.val < root.val:  #pq < root.val 在左子树里找
            left = self.lowestCommonAncestor(root.left, p, q)  #要把公共祖先找到的，返回上来，所以要left接住
            if left: return left
        if p.val > root.val and q.val > root.val:  #pq > root.val  在右子树里找
            right = self.lowestCommonAncestor(root.right, p, q)
            if right: return right
        return root   #剩下的情况就是root在pq之间了

迭代

class Solution:
    """二叉搜索树的最近公共祖先 迭代法"""

    def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':
        while True:
            if root.val > p.val and root.val > q.val:
                root = root.left
            elif root.val < p.val and root.val < q.val:
                root = root.right
            else:
                return root

701.二叉搜索树中的插入操作

题目链接

其实这道题目其实是一道简单题目，但是题目中的提示：有多种有效的插入方式，还可以重构二叉搜索树，一下子吓退了不少人，瞬间感觉题目复杂了很多。

其实可以不考虑题目中提示所说的改变树的结构的插入方式。就插在叶子结点就行了，不改变二叉搜索树的结构。

思路就变成了，只要遍历二叉搜索树，找到空节点 插入元素就可以了，那么这道题其实就简单了。 再分解一下，找到叶子的位置，创建val == val结的点，然后把它插在相应位置就行了。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def insertIntoBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
        if root == None:                 #找到叶子结点的位置
            node = TreeNode(val)         #创建新节点
            return node                  #有返回值，可以利用返回值完成新加入的节点与其父节点的赋值操作
        if root.val < val:
            root.right = self.insertIntoBST(root.right, val)
        if root.val > val:
            root.left = self.insertIntoBST(root.left, val)

        return root

就是root传进来，根据二叉搜索树的 left

450.删除二叉搜索树中的节点

题目链接
这道题不是很难，就是要分情况去动这个树的的结构，各种情况都写进代码里了

# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def deleteNode(self, root: Optional[TreeNode], key: int) -> Optional[TreeNode]:
        if root == None: return None
        if root.val == key:
            #第一种，要删除的结点是叶子结点，左空 右空
            if not root.left and not root.right:
                return None  #为什么return None, 因为删除的是叶子，叶子没有后继
            #第二种，要删除结点的左子不空，右子空  返回左子
            elif root.left and not root.right:
                return root.left
            #第三种，要删除的结点的左子空， 右子不空，返回右子
            elif not root.left and root.right:
                return root.right
            #第四种，要删除的结点的左子不空，右子不空，要把左子树加到右子树最左边的一个结点上
            else:
                curr = root.right
                while curr.left != None:  #去找，要删除的结点 右子树的 最左边的一个结点
                    curr = curr.left      #此时， curr指向  要删除的结点的  右子树的  最左的孩子

                curr.left = root.left     #要删除的左子树嫁接到右子树的最左边的一个孩子
                return root.right         #因为 把要删除的左子树嫁接到右子树了, 返回右子树

        if root.val > key:
            root.left = self.deleteNode(root.left, key)
        if root.val < key:
            root.right = self.deleteNode(root.right, key)
        
        return root

普通二叉树的删除方式

这里我在介绍一种通用的删除，普通二叉树的删除方式（没有使用搜索树的特性，遍历整棵树），用交换值的操作来删除目标节点。

代码中目标节点（要删除的节点）被操作了两次：

第一次是和目标节点的右子树最左面节点交换。
第二次直接被NULL覆盖了。
思路有点绕，感兴趣的同学可以画图自己理解一下。

代码如下：（关键部分已经注释）

class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        if (root == nullptr) return root;
        if (root->val == key) {
            if (root->right == nullptr) { // 这里第二次操作目标值：最终删除的作用
                return root->left;
            }
            TreeNode *cur = root->right;
            while (cur->left) {
                cur = cur->left;
            }
            swap(root->val, cur->val); // 这里第一次操作目标值：交换目标值其右子树最左面节点。
        }
        root->left = deleteNode(root->left, key);
        root->right = deleteNode(root->right, key);
        return root;
    }
};