《Pytorch深度学习和图神经网络(卷 1)》学习笔记——第七章

这一章内容有点丰富，多用了一些时间，实例就有四五个。
这章内容是真多啊！（学完之后又回到开头感叹）

大脑分级处理机制：

将图像从基础像素到局部信息再到整体信息
即将图片由低级特征到高级特征进行逐级计算，逐级累计。

视觉神经网络中的离散积分

计算机中对图片的处理可以理解为离散微积分的过程。
利用卷积操作对图片的局部信息处理，生成低级特征
对低级特征进行多次卷积操作，生成中级特征、高级特征
将多个局部信息的高级特征组合到一起，生成最终的解释结果
这就是卷积神经网络

比全连接权重更少，对数据进行基于区域小规模运算，改善了难收敛，提高了泛化能力。

可以用全连接网络为参照，卷积神经网络更像是多个全连接片段的组合。

卷积网络输出的每个节点，都是原数据中局部区域节点经过神经元计算后得到的结果。
全连接网络输出的每个节点，都是原数据中全部节点经过神经元计算后得到的结果。
因此卷积神经网络包含的局部信息更为明显，在计算机视觉领域被广泛应用。

1D卷积常用来处理文本或特征数值类数据
2D卷积常用来处理平面图片类数据
3D卷积常用来处理立体图像或视频类数据

实例分析：Sobel算子的原理
Sobel算子其实是卷积操作中的一个典型例子，手动配置好权重的卷积核，实现图片的边缘检测。
a为水平 b为垂直方向

a=[[-1,0,1],
	[-2,0,2],
	[-1,0,1]]
b=[[1,2,1],
	[0,0,0],
	[-1,-2,1]]

新生成的像素值不一定在0到256之间，要进行归一化然后乘256。

sobel算子原理

第一行（-1，0，-1）的卷积核进行1D卷积时，本质上是计算相隔像素之间的距离。
1256788卷积后44221，少了2位因为核的缘故。
如果将像素差值数据用图片的方式显示出来，就是轮廓图片。
第二行（-2，0，2）的同上，只不过将距离放大2倍，起到增强效果。
思想是，对卷积核3行像素差值再做加权处理，以第二行像素差值为中心，距离中心点近影响越大的原理，对第二行加强，在结果中产生主要影响。
第二行与第一行相同也可以产生轮廓，OpenCV中有scharr函数…实sobel变了权重。
垂直其实就是水平算子的转置。

深层神经网络中的卷积核

这时的卷积核是经过大量样本训练之后计算出来的，若生成了若干个有特定功能的卷积核，有的计算像素差值，提取轮廓特征；有的计算平均值，提取纹理特征。

卷积分

$$y=3x+2.$$
$$y=2x^2+3x-1.$$
代数的角度理解是相乘
$$y=6x^3+13x^2+3x-2.$$

卷积神经网络的实现

卷积的操作类型：
窄卷积、同卷积、全卷积。
计算规则：
$$H_{out}=\frac{H_{in}+2\times padding[0]-dilation[0]\times (kerne{l}_{s}ize[0]-1)-1}{stride[0]}+1.$$
$$W_{out}=\frac{W_{in}+2\times padding[1]-dilation[1]\times (kerne{l}_{s}ize[1]-1)-1}{stride[1]}+1.$$

实例6：卷积函数应用

观察卷积核个数和图像通道数对卷积核维度的影响。

import torch
# [batch, in_channels, in_height, in_width] [训练时一个batch的图片数量, 图像通道数, 图片高度, 图片宽度]
input1 = torch.ones([1, 1, 5, 5])
input2 = torch.ones([1, 2, 5, 5])
input3 = torch.ones([1, 1, 4, 4])
# [ out_channels, in_channels，filter_height, filter_width] [卷积核个数，图像通道数，卷积核的高度，卷积核的宽度]
filter1 =  torch.tensor([-1.0,0,0,-1]).reshape([1, 1, 2, 2])
filter2 =  torch.tensor([-1.0,0,0,-1,-1.0,0,0,-1]).reshape([2,1,2, 2])
filter3 =  torch.tensor([-1.0,0,0,-1,-1.0,0,0,-1,-1.0,0,0,-1]).reshape([3,1,2, 2])
filter4 =  torch.tensor([-1.0,0,0,-1,-1.0,0,0,-1,
                                   -1.0,0,0,-1,
                                   -1.0,0,0,-1]).reshape([2, 2, 2, 2])
filter5 =  torch.tensor([-1.0,0,0,-1,-1.0,0,0,-1]).reshape([1,2, 2, 2])

print(filter1)
print(filter2)
print(filter3)
print(filter4)
print(filter5)
#tensor([[[[-1.,  0.],
#          [ 0., -1.]]]])
卷积核个数X图像通道数=1，共一个卷积核单通道
#tensor([[[[-1.,  0.],
#          [ 0., -1.]]],
#
#        [[[-1.,  0.],
#          [ 0., -1.]]]])
2X1=2，两个卷积核单通道
#tensor([[[[-1.,  0.],
#          [ 0., -1.]]],
#
#        [[[-1.,  0.],
#          [ 0., -1.]]],
#
#        [[[-1.,  0.],
#          [ 0., -1.]]]])
3X1=3，三个卷积核，单通道
#tensor([[[[-1.,  0.],
#          [ 0., -1.]],
#         [[-1.,  0.],
#          [ 0., -1.]]],
#
#        [[[-1.,  0.],
#          [ 0., -1.]],
#         [[-1.,  0.],
#          [ 0., -1.]]]])
2X2=4，两个卷积核且两个通道
#tensor([[[[-1.,  0.],
#          [ 0., -1.]],
#         [[-1.,  0.],
#          [ 0., -1.]]]])
1X2=2，一个卷积核且两个通道
[ ]里为一个通道，[[]]里为一个卷积核

观察padding填充，padding=(1,2)是(上,下)填充，padding=1，为对周围填充一圈。

#验证padding补0的规则 ——上下左右都补0
padding1 = torch.nn.functional.conv2d(input1, torch.ones([1,1,1,1]), stride=1, padding=1)
print(padding1)
#tensor([[[[0., 0., 0., 0., 0., 0., 0.],   
#          [0., 1., 1., 1., 1., 1., 0.],   
#          [0., 1., 1., 1., 1., 1., 0.],   
#          [0., 1., 1., 1., 1., 1., 0.],   
#          [0., 1., 1., 1., 1., 1., 0.],   
#          [0., 1., 1., 1., 1., 1., 0.],   
#          [0., 0., 0., 0., 0., 0., 0.]]]])
padding2 = torch.nn.functional.conv2d(input1, torch.ones([1,1,1,1]), stride=1, padding=(1,2))
print(padding2)
#tensor([[[[0., 0., 0., 0., 0., 0., 0., 0., 0.],
#          [0., 0., 1., 1., 1., 1., 1., 0., 0.],
#          [0., 0., 1., 1., 1., 1., 1., 0., 0.],
#          [0., 0., 1., 1., 1., 1., 1., 0., 0.],
#          [0., 0., 1., 1., 1., 1., 1., 0., 0.],
#          [0., 0., 1., 1., 1., 1., 1., 0., 0.],
#          [0., 0., 0., 0., 0., 0., 0., 0., 0.]]]])

几个卷积核生成几个特征图，几个通道数相加为一个通道图

op1:单卷积核单通道，生成1个feature map
 tensor([[[[-1., -1., -1.],
          [-1., -2., -2.],
          [-1., -2., -2.]]]])
op2:双卷积核单通道，生成2个feature map
 tensor([[[[-1., -1., -1.],
          [-1., -2., -2.],
          [-1., -2., -2.]],

         [[-1., -1., -1.],
          [-1., -2., -2.],
          [-1., -2., -2.]]]])
op3:三卷积核单通道，生成3个feature map
 tensor([[[[-1., -1., -1.],
          [-1., -2., -2.],
          [-1., -2., -2.]],

         [[-1., -1., -1.],
          [-1., -2., -2.],
          [-1., -2., -2.]],

         [[-1., -1., -1.],
          [-1., -2., -2.],
          [-1., -2., -2.]]]])
op4:双卷积核双通道，生成2个feature map
 tensor([[[[-2., -2., -2.],
          [-2., -4., -4.],
          [-2., -4., -4.]],

         [[-2., -2., -2.],
          [-2., -4., -4.],
          [-2., -4., -4.]]]]) 
op5:单卷积核双通道，生成1个feature map
 tensor([[[[-2., -2., -2.],
          [-2., -4., -4.],
          [-2., -4., -4.]]]]) 
---------------------------------------
op1:
 tensor([[[[-1., -1., -1.],
          [-1., -2., -2.],
          [-1., -2., -2.]]]]) 
op6:不加padding
 tensor([[[[-2., -2.],
          [-2., -2.]]]]) 

自行设计了单卷积核三通道，证明上述分析。

# [batch, in_channels, in_height, in_width] [训练时一个batch的图片数量, 图像通道数, 图片高度, 图片宽度]5])
input8 = torch.ones([1, 3, 5, 5])
op8 = torch.nn.functional.conv2d(input8, filter8, stride=2, padding=1) 
# [ out_channels, in_channels，filter_height, filter_width] [卷积核个数，图像通道数，卷积核的高度，卷积核的宽度]
filter8= torch.tensor([
                        [[[-1.,  0.],
                          [ 0., -1.]],
                         [[-1.,  0.],
                          [ 0., -1.]],
                         [[-1.,  0.],
                          [ 0., -1.]]]
                      ]).reshape([1,3, 2, 2])
print("op8:\n",op8,filter8)
tensor([[[[-3., -3., -3.],
          [-3., -6., -6.],
          [-3., -6., -6.]]]]) 

完整代码：

import torch
# [batch, in_channels, in_height, in_width] [训练时一个batch的图片数量, 图像通道数, 图片高度, 图片宽度]
input1 = torch.ones([1, 1, 5, 5])
input2 = torch.ones([1, 2, 5, 5])
input3 = torch.ones([1, 1, 4, 4])
# [ out_channels, in_channels，filter_height, filter_width] [卷积核个数，图像通道数，卷积核的高度，卷积核的宽度]
filter1 =  torch.tensor([-1.0,0,0,-1]).reshape([2, 2, 1, 1])
filter2 =  torch.tensor([-1.0,0,0,-1,-1.0,0,0,-1]).reshape([2,1,2, 2])
filter3 =  torch.tensor([-1.0,0,0,-1,-1.0,0,0,-1,-1.0,0,0,-1]).reshape([3,1,2, 2])
filter4 =  torch.tensor([-1.0,0,0,-1,-1.0,0,0,-1,
                                   -1.0,0,0,-1,
                                   -1.0,0,0,-1]).reshape([2, 2, 2, 2])
filter5 =  torch.tensor([-1.0,0,0,-1,-1.0,0,0,-1]).reshape([1,2, 2, 2])

#class torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True)
#condv = torch.nn.Conv2d(1,1,kernel_size=1,padding=1, bias=False)
#condv.weight = torch.nn.Parameter(torch.ones([1,1,1,1]))
#padding1 = condv(input1)
#print(padding1)

#验证padding补0的规则 ——上下左右都补0
padding1 = torch.nn.functional.conv2d(input1, torch.ones([1,1,1,1]), stride=1, padding=1)
print(padding1)


padding2 = torch.nn.functional.conv2d(input1, torch.ones([1,1,1,1]), stride=1, padding=(1,2))
print(padding2)

##1个通道输入，生成1个feature map
#filter1 =  torch.tensor([-1.0,0,0,-1]).reshape([1, 1, 2, 2])
#op1 = torch.nn.functional.conv2d(input1, filter1, stride=2, padding=1)
#print('\n')
#print(padding1)
#print(filter1)
#print(op1)

#torch.nn.Conv2d(in_channels=1, out_channels=6, kernel_size=5)
#torch.nn.functional.conv1d(input, weight, bias=None, stride=1, padding=0, dilation=1, groups=1)
#torch.nn.functional.conv2d(input, weight, bias=None, stride=1, padding=0, dilation=1, groups=1)





op1 = torch.nn.functional.conv2d(input1, filter1, stride=2, padding=1) #1个通道输入，生成1个feature map
op2 = torch.nn.functional.conv2d(input1, filter2, stride=2, padding=1) #1个通道输入，生成2个feature map
op3 = torch.nn.functional.conv2d(input1, filter3, stride=2, padding=1) #1个通道输入，生成3个feature map

op4 = torch.nn.functional.conv2d(input2, filter4, stride=2, padding=1) # 2个通道输入，生成2个feature
op5 = torch.nn.functional.conv2d(input2, filter5, stride=2, padding=1) # 2个通道输入，生成一个feature map

op6 = torch.nn.functional.conv2d(input1, filter1, stride=2, padding=0) # 5*5 对于pading不同而不同


print("op1:\n",op1,filter1)#1-1  后面补0
print("------------------")

print("op2:\n",op2,filter2) #1-2多卷积核 按列取
print("op3:\n",op3,filter3) #1-3
print("------------------")

print("op4:\n",op4,filter4)#2-2    通道叠加
print("op5:\n",op5,filter5)#2-1
print("------------------")

print("op1:\n",op1,filter1)#1-1
print("op6:\n",op6,filter1)

实例7：使用卷积提取图片的轮廓

shape为（3264，2448，3）
transforms.ToTensor类能将图片转化为Pytorch所支持的形状（【通道数，高，宽】），同时将图片数值归一化为0到1的小数
sobelfilter = torch.tensor([[-1.0,0,1], [-2,0,2], [-1.0,0,1.0]]*3).reshape([1,3,3, 3])
三通道就乘三

import matplotlib.pyplot as plt # plt 用于显示图片
import matplotlib.image as mpimg # mpimg 用于读取图片
import torch
import torchvision.transforms as transforms

myimg = mpimg.imread('pytorch\chapter7\img.jpg') # 读取和代码处于同一目录下的图片
plt.imshow(myimg) # 显示图片
plt.axis('off') # 不显示坐标轴
plt.show()
print(myimg.shape)
(3264, 2448, 3)

pil2tensor = transforms.ToTensor()
rgb_image = pil2tensor(myimg)
print(rgb_image[0][0])
tensor([0.8471, 0.8471, 0.8471,  ..., 0.6824, 0.6824, 0.6824])
print(rgb_image.shape)
torch.Size([3, 3264, 2448])

sobelfilter =  torch.tensor([[-1.0,0,1],  [-2,0,2],  [-1.0,0,1.0]]*3).reshape([1,3,3, 3])
print(sobelfilter)
tensor([[[[-1.,  0.,  1.],
          [-2.,  0.,  2.],
          [-1.,  0.,  1.]],

         [[-1.,  0.,  1.],
          [-2.,  0.,  2.],
          [-1.,  0.,  1.]],

         [[-1.,  0.,  1.],
          [-2.,  0.,  2.],
          [-1.,  0.,  1.]]]])

op =torch.nn.functional.conv2d(rgb_image.unsqueeze(0), sobelfilter, stride=3,padding = 1) #3个通道输入，生成1个feature map

#对卷积结果进行处理，数据不能保证在0到255内，必须归一化再乘255
ret = (op - op.min()).div(op.max() - op.min())
ret =ret.clamp(0., 1.).mul(255).int()
print(ret)
tensor([[[[193,  99,  99,  ...,  99,  99,  99],
          [225,  99,  99,  ...,  99, 100,  99],
          [224,  99,  99,  ...,  99, 100,  99],
          ...,
          [177,  97, 100,  ...,  95, 100, 100],
          [178, 100, 100,  ..., 100,  98,  97],
          [177,  99,  98,  ...,  96, 100,  98]]]], dtype=torch.int32)


plt.imshow(ret.squeeze(),cmap='Greys_r') # 显示图片
plt.axis('off') # 不显示坐标轴
plt.show()

op=torch.nn.functional.max_pool2d(op,kernel_size =5, stride=5)
op = op.transpose(1,3).transpose(1,2)
print(op.shape)
torch.Size([1, 217, 163, 1])

关于灰度图，对3个通道的图片取平均值，或计算图片0维上的平均值。

r_image=rgb_image[0]
g_image=rgb_image[0]
b_image=rgb_image[0]
grayscale_image=(r_image=rgb_image[0]+g_image=rgb_image[0]+b_image=rgb_image[0]).div(3.0)
plt.imshow(grayscale_image,cmap='Greys_r') # 显示图片
plt.axis('off') # 不显示坐标轴
plt.show()
或者
plt.imshow(rgb_image.mean(),cmap='Greys_r') # 显示图片
plt.axis('off') # 不显示坐标轴
plt.show()

深层卷积神经网络

是多个卷积层和若干其他的神经网络叠加在一起的，原始的主要是输入、卷积、池化、全连接（或全局平均池化层）等部分组成。
输入层：将每个像素作为一个特征节点输入网络
卷积层：多个滤波器组合而成
池化层：将卷积结果降维
全局平均池化层：对生成的特征图取全局平均值，该层也可以用全连接网络代替
输出层：网络需要将数据分成几类，就输出几个节点。

卷积神经网络的反向传播

卷积操作反向求导时，要将特征图做一次padding再与转置后的卷积核做一次卷积操作，即可得到输入端的误差，实现误差的反向传播。

池化操作

主要目的是降维，在保持原有特征的基础上最大限度的将数组的维度变小。
池化只关心滤波器的尺寸，不考虑内部的值，算法是将滤波器映射区域内的像素点取平均值或最大值。
有均值池化（对背景信息更敏感）和最大池化（对纹理特征信息更敏感）。
也有两种实现方式，函数调用和类的方式

实例8：池化函数的应用

手动生成一个4x4的矩阵来模拟图片，两个通道，定义一个2x2的滤波器
pooling3是常用的操作手法，也称全局池化法，与输入数据经两次平均值计算结果数值一致，只有形状不同。

import torch

img=torch.tensor([ [ [0.,0.,0.,0.],[1.,1.,1.,1.],[2.,2.,2.,2.],[3.,3.,3.,3.] ],
                   [ [4.,4.,4.,4.],[5.,5.,5.,5.],[6.,6.,6.,6.],[7.,7.,7.,7.] ]
                 ]).reshape([1,2,4,4])
print(img)
#两个通道
tensor([[[[0., 0., 0., 0.],
          [1., 1., 1., 1.],
          [2., 2., 2., 2.],
          [3., 3., 3., 3.]],

         [[4., 4., 4., 4.],
          [5., 5., 5., 5.],
          [6., 6., 6., 6.],
          [7., 7., 7., 7.]]]])
print(img[0][0])
tensor([[0., 0., 0., 0.],
        [1., 1., 1., 1.],
        [2., 2., 2., 2.],
        [3., 3., 3., 3.]])
print(img[0][1])
tensor([[4., 4., 4., 4.],
        [5., 5., 5., 5.],
        [6., 6., 6., 6.],
        [7., 7., 7., 7.]])
#torch.nn.functional.avg_pool2d(input, kernel_size, stride=None, padding=0, ceil_mode=False, count_include_pad=True)
pooling=torch.nn.functional.max_pool2d(img,kernel_size =2)
print("pooling:\n",pooling)
pooling:
 tensor([[[[1., 1.],
          [3., 3.]],

         [[5., 5.],
          [7., 7.]]]])
pooling1=torch.nn.functional.max_pool2d(img,kernel_size =2,stride=1)
print("pooling1:\n",pooling1)
pooling1:
 tensor([[[[1., 1., 1.],
          [2., 2., 2.],
          [3., 3., 3.]],

         [[5., 5., 5.],
          [6., 6., 6.],
          [7., 7., 7.]]]])

pooling2=torch.nn.functional.avg_pool2d(img,kernel_size =4,stride=1,padding=1)
print("pooling2:\n",pooling2)
pooling2:
 tensor([[[[0.5625, 0.7500, 0.5625],
          [1.1250, 1.5000, 1.1250],
          [1.1250, 1.5000, 1.1250]],

         [[2.8125, 3.7500, 2.8125],
          [4.1250, 5.5000, 4.1250],
          [3.3750, 4.5000, 3.3750]]]])
pooling3=torch.nn.functional.avg_pool2d(img,kernel_size =4)
print("pooling3:\n",pooling3)
pooling3:
 tensor([[[[1.5000]],

         [[5.5000]]]])
m1 = img.mean(3)
print("第1次平均值结果:\n",m1)
第1次平均值结果:
 tensor([[[0., 1., 2., 3.],
         [4., 5., 6., 7.]]])
print("第2次平均值结果:\n",m1.mean(2))
第2次平均值结果:
 tensor([[1.5000, 5.5000]])

上述可以修改，结果等价

img=torch.tensor( [ [0.,0.,0.,0.],[1.,1.,1.,1.],[2.,2.,2.,2.],[3.,3.,3.,3.] ,
                    [4.,4.,4.,4.],[5.,5.,5.,5.],[6.,6.,6.,6.],[7.,7.,7.,7.] ]
                 ).reshape([2,4,4])
m1 = img.mean(2)
print("第2次平均值结果:\n",m1.mean(1))

实例9：搭建卷积神经网络

对第六章实例5进行修改，将2个全连接变为全局平均池化层。
将最后3个全连接层，改为1个卷积层和1个全局平均池化层，卷积核由5改为3
替换一下网络类定义就行了

class myConNet(torch.nn.Module):
    def __init__(self):
        super(myConNet, self).__init__()
        #定义卷积层
        self.conv1 = torch.nn.Conv2d(in_channels=1, out_channels=6, kernel_size=3)
        self.conv2 = torch.nn.Conv2d(in_channels=6, out_channels=12, kernel_size=3)
        self.conv3 = torch.nn.Conv2d(in_channels=12, out_channels=10, kernel_size=3)

    def forward(self, t):#搭建正向结构
        #第一层卷积和池化处理
        t = self.conv1(t)
        t = F.relu(t)
        t = F.max_pool2d(t, kernel_size=2, stride=2)
        #第二层卷积和池化处理
        t = self.conv2(t)
        t = F.relu(t)
        t = F.max_pool2d(t, kernel_size=2, stride=2)

        #第三层卷积和池化处理
        t = self.conv3(t)
        t = F.avg_pool2d(t, kernel_size=t.shape[-2:], stride=t.shape[-2:])

        return t.reshape(t.shape[:2])
    #训练完记得
    torch.save(network.state_dict(),'./CNNFashionMNIST2.pth')#保存模型
    network.load_state_dict(torch.load( './CNNFashionMNIST2.pth'))#加载模型

测试结果：
Accuracy of T-shirt : 66 %
Accuracy of Trouser : 92 %
Accuracy of Pullover : 72 %
Accuracy of Dress : 80 %
Accuracy of Coat : 68 %
Accuracy of Sandal : 94 %
Accuracy of Shirt : 58 %
Accuracy of Sneaker : 91 %
Accuracy of Bag : 95 %
Accuracy of Ankle_Boot : 96 %
Accuracy of all : 81 %
对比之前的模型在某些类别上提升很明显：
Accuracy of Trouser : 90 %
Accuracy of Pullover : 49 %
Accuracy of Dress : 85 %
Accuracy of Coat : 81 %
Accuracy of Sandal : 92 %
Accuracy of Shirt : 42 %
Accuracy of Sneaker : 91 %
Accuracy of Bag : 94 %
Accuracy of Ankle_Boot : 94 %
Accuracy of all : 80 %

循环神经网络(Recurrent Neural Network ,RNN)

是一个具有记忆功能的网络，它可以发现样本彼此间的相互关系，它多用于处理带有序列特征的样本数据。
人的记忆原理。
婴儿虽然说话能表达意思，但有时会很奇怪，要零食的时候说把“我要”说成“要我”，大脑对这两个字是有先后顺序的。
当获得“我来找你玩游”的时候，大脑语言模型会自动匹配“戏”，而不是游泳、游乐。
用下列伪代码表示逻辑：
（input我+empty-input）→output我
（input来+output我）→output来
（input找+output来）→output找
（input你+output找）→output你
如让小孩背三字经，名俱扬下一句很容易说，问上一句是什么，小孩从头背了一遍。
对于序列化的特征任务，如情感分析、关键字提取、语音识别、机器翻译、股票分析等等适合循环神经网络来解决。

基本结构是，将全连接网络的输出节点复制一份，传回到输入节点，与输入数据一起进行下一次计算。

实例10： 简单循环神经网络实现——设计一个退位减法器

定义基本函数，手写sigmoid及其导数（用于反向传播）

import copy, numpy as np
np.random.seed(0) #随机数生成器的种子，可以每次得到一样的值
# compute sigmoid nonlinearity
def sigmoid(x): #激活函数
    output = 1/(1+np.exp(-x))
    return output
# convert output of sigmoid function to its derivative
def sigmoid_output_to_derivative(output):#激活函数的导数
    return output*(1-output)

建立二进制映射，将减法允许最大值设置为255，即8位二级制，定义int与二进制之间的映射组int2binary。

int2binary = {} #整数到其二进制表示的映射
binary_dim = 8 #暂时制作256以内的减法
## 计算0-256的二进制表示
largest_number = pow(2,binary_dim)
binary = np.unpackbits(
    np.array([range(largest_number)],dtype=np.uint8).T,axis=1)
for i in range(largest_number):
    int2binary[i] = binary[i]
print(int2binary)
{0: array([0, 0, 0, 0, 0, 0, 0, 0], dtype=uint8), 1: array([0, 0, 0, 0, 0, 0, 0, 1], dtype=uint8), 2: array([0, 0, 0, 0, 0, 0, 
1, 0], dtype=uint8), 3: array([0, 0, 0, 0, 0, 0, 1, 1], dtype=uint8), 4: array([0, 0, 0, 0, 0, 1, 0, 0], dtype=uint8), 5: array([0, 0, 0, 0, 0, 1, 0, 1], dtype=uint8)..........}

定义参数
隐藏层的权重为synapse_0，循环节点的权重为synapse_h（输入16节点、输出16节点），输出层的权重为synapse_1（输入16节点输出1节点）。
synapse_0_update在前面很少见，是因为它被隐藏在优化器里了，这里是自动手写，需要定义一组变量来存放反向优化参数时需要调整的值。对于前面3个权重synapse_0到3。

# input variables
alpha = 0.9 #学习速率
input_dim = 2 #输入的维度是2
hidden_dim = 16 
output_dim = 1 #输出维度为1

# initialize neural network weights
synapse_0 = (2*np.random.random((input_dim,hidden_dim)) - 1)*0.05 #维度为2*16， 2是输入维度，16是隐藏层维度
synapse_1 = (2*np.random.random((hidden_dim,output_dim)) - 1)*0.05
synapse_h = (2*np.random.random((hidden_dim,hidden_dim)) - 1)*0.05
# => [-0.05, 0.05)，

# 用于存放反向传播的权重更新值
synapse_0_update = np.zeros_like(synapse_0)
synapse_1_update = np.zeros_like(synapse_1)
synapse_h_update = np.zeros_like(synapse_h)

准备样本数据
建立循环生成样本数据，先生成两个数a和b。如果a小于b，就交换位置，保证被减数大。计算出相减结果c，将3个数转化为二进制，为模型计算做准备。
模型初始化
初始化输出值为0，初始化总误差为0，定义layer_2_deltas为存储反向传播过程中的循环层的误差，layer_1_values为隐藏层的输出值。由于第一个数据输入时，没有前面隐藏层输出值来作为本次的输入，因此需要定义一个初始值，这里初始化为0.1。
正向传播
future_layer_1_delta = np.zeros(hidden_dim)是为了反向传播准备的初始化，反向传播是从正向传播的最后一次计算开始反向计算误差，它没有后一次的输出，因此要初始化一个值作为其后一次的输入，这里初始化为0。
反向传播
开始从高位往回遍历，一次对每一位的所有层计算误差，并对权重求偏导，得到调整值，最后将每一位算出的各层权重的调整值加在一起乘以学习率来更新各层参数。每次更新完后中间变量会清零。
输出结果
每运行800次输出一次结果。

# training 
for j in range(10000):
    
    #生成一个数字a
    a_int = np.random.randint(largest_number) 
    #生成一个数字b,b的最大值取的是largest_number/2,作为被减数，让它小一点。
    b_int = np.random.randint(largest_number/2) 
    #如果生成的b大了，那么交换一下
    if a_int<b_int:
        tt = a_int
        b_int = a_int
        a_int=tt
    
    a = int2binary[a_int] # binary encoding
    b = int2binary[b_int] # binary encoding    
    # true answer
    c_int = a_int - b_int
    c = int2binary[c_int]
    
    # 存储神经网络的预测值
    d = np.zeros_like(c)
    overallError = 0 #每次把总误差清零
    
    layer_2_deltas = list() #存储每个时间点输出层的误差
    layer_1_values = list() #存储每个时间点隐藏层的值
    
    layer_1_values.append(np.ones(hidden_dim)*0.1) # 一开始没有隐藏层，所以初始化一下原始值为0.1
    
    # moving along the positions in the binary encoding
    for position in range(binary_dim):#循环遍历每一个二进制位
        
        # generate input and output
        X = np.array([[a[binary_dim - position - 1],b[binary_dim - position - 1]]])#从右到左，每次去两个输入数字的一个bit位
        y = np.array([[c[binary_dim - position - 1]]]).T#正确答案
        # hidden layer (input ~+ prev_hidden)
        layer_1 = sigmoid(np.dot(X,synapse_0) + np.dot(layer_1_values[-1],synapse_h))#（输入层 + 之前的隐藏层） -> 新的隐藏层，这是体现循环神经网络的最核心的地方！！！
        # output layer (new binary representation)
        layer_2 = sigmoid(np.dot(layer_1,synapse_1)) #隐藏层 * 隐藏层到输出层的转化矩阵synapse_1 -> 输出层
        
        layer_2_error = y - layer_2 #预测误差
        layer_2_deltas.append((layer_2_error)*sigmoid_output_to_derivative(layer_2)) #把每一个时间点的误差导数都记录下来
        overallError += np.abs(layer_2_error[0])#总误差
    
        d[binary_dim - position - 1] = np.round(layer_2[0][0]) #记录下每一个预测bit位
        
        # store hidden layer so we can use it in the next timestep
        layer_1_values.append(copy.deepcopy(layer_1))#记录下隐藏层的值，在下一个时间点用
    
    future_layer_1_delta = np.zeros(hidden_dim)
    
    #反向传播，从最后一个时间点到第一个时间点
    for position in range(binary_dim):
        
        X = np.array([[a[position],b[position]]]) #最后一次的两个输入
        layer_1 = layer_1_values[-position-1] #当前时间点的隐藏层
        prev_layer_1 = layer_1_values[-position-2] #前一个时间点的隐藏层
        
        # error at output layer
        layer_2_delta = layer_2_deltas[-position-1] #当前时间点输出层导数
        # error at hidden layer
        # 通过后一个时间点（因为是反向传播）的隐藏层误差和当前时间点的输出层误差，计算当前时间点的隐藏层误差
        layer_1_delta = (future_layer_1_delta.dot(synapse_h.T) + layer_2_delta.dot(synapse_1.T)) * sigmoid_output_to_derivative(layer_1)
        
        
       # 等到完成了所有反向传播误差计算， 才会更新权重矩阵，先暂时把更新矩阵存起来。
        synapse_1_update += np.atleast_2d(layer_1).T.dot(layer_2_delta)
        synapse_h_update += np.atleast_2d(prev_layer_1).T.dot(layer_1_delta)
        synapse_0_update += X.T.dot(layer_1_delta)
        
        future_layer_1_delta = layer_1_delta
    
    # 完成所有反向传播之后，更新权重矩阵。并把矩阵变量清零
    synapse_0 += synapse_0_update * alpha
    synapse_1 += synapse_1_update * alpha
    synapse_h += synapse_h_update * alpha
    synapse_0_update *= 0
    synapse_1_update *= 0
    synapse_h_update *= 0
   
    # print out progress
    if(j % 800 == 0):
        #print(synapse_0,synapse_h,synapse_1)
        print("总误差:" + str(overallError))
        print("Pred:" + str(d))
        print("True:" + str(c))
        out = 0
        for index,x in enumerate(reversed(d)):
            out += x*pow(2,index)
        print(str(a_int) + " - " + str(b_int) + " = " + str(out))
        print("------------")
总误差:[3.97242498]
Pred:[0 0 0 0 0 0 0 0]
True:[0 0 0 0 0 0 0 0]
9 - 9 = 0
------------
总误差:[2.1721182]
Pred:[0 0 0 0 0 0 0 0]
True:[0 0 0 1 0 0 0 1]
17 - 0 = 0
------------
总误差:[1.1082385]
Pred:[0 0 0 0 0 0 0 0]
True:[0 0 0 0 0 0 0 0]
59 - 59 = 0
------------
总误差:[0.18727913]
Pred:[0 0 0 0 0 0 0 0]
True:[0 0 0 0 0 0 0 0]
19 - 19 = 0
------------
总误差:[0.21914293]
Pred:[0 0 0 0 0 0 0 0]
True:[0 0 0 0 0 0 0 0]
71 - 71 = 0
------------
总误差:[0.26861004]
Pred:[0 0 1 1 1 1 0 0]
True:[0 0 1 1 1 1 0 0]
71 - 11 = 60
------------
总误差:[0.11815367]
Pred:[1 0 0 0 0 0 0 0]
True:[1 0 0 0 0 0 0 0]
230 - 102 = 128
------------
总误差:[0.2927243]
Pred:[0 1 1 1 0 0 0 1]
True:[0 1 1 1 0 0 0 1]
160 - 47 = 113
------------
总误差:[0.04298749]
Pred:[0 0 0 0 0 0 0 0]
True:[0 0 0 0 0 0 0 0]
3 - 3 = 0
------------
总误差:[0.04243453]
Pred:[0 0 0 0 0 0 0 0]
True:[0 0 0 0 0 0 0 0]
17 - 17 = 0
------------
总误差:[0.04588656]
Pred:[1 0 0 1 0 1 1 0]
True:[1 0 0 1 0 1 1 0]
167 - 17 = 150
------------
总误差:[0.08098026]
Pred:[1 0 0 1 1 0 0 0]
True:[1 0 0 1 1 0 0 0]
204 - 52 = 152
------------
总误差:[0.03262333]
Pred:[1 1 0 0 0 0 0 0]
True:[1 1 0 0 0 0 0 0]
209 - 17 = 192
------------

从训练结果可以看出，一开始不准确，多次迭代后就精准了。

完整代码：

import copy, numpy as np
np.random.seed(0) #随机数生成器的种子，可以每次得到一样的值
# compute sigmoid nonlinearity
def sigmoid(x): #激活函数
    output = 1/(1+np.exp(-x))
    return output
# convert output of sigmoid function to its derivative
def sigmoid_output_to_derivative(output):#激活函数的导数
    return output*(1-output)


int2binary = {} #整数到其二进制表示的映射
binary_dim = 8 #暂时制作256以内的减法
## 计算0-256的二进制表示
largest_number = pow(2,binary_dim)
binary = np.unpackbits(
    np.array([range(largest_number)],dtype=np.uint8).T,axis=1)
for i in range(largest_number):
    int2binary[i] = binary[i]

# input variables
alpha = 0.9 #学习速率
input_dim = 2 #输入的维度是2
hidden_dim = 16 
output_dim = 1 #输出维度为1

# initialize neural network weights
synapse_0 = (2*np.random.random((input_dim,hidden_dim)) - 1)*0.05 #维度为2*16， 2是输入维度，16是隐藏层维度
synapse_1 = (2*np.random.random((hidden_dim,output_dim)) - 1)*0.05
synapse_h = (2*np.random.random((hidden_dim,hidden_dim)) - 1)*0.05
# => [-0.05, 0.05)，

# 用于存放反向传播的权重更新值
synapse_0_update = np.zeros_like(synapse_0)
synapse_1_update = np.zeros_like(synapse_1)
synapse_h_update = np.zeros_like(synapse_h)

# training 
for j in range(10000):
    
    #生成一个数字a
    a_int = np.random.randint(largest_number) 
    #生成一个数字b,b的最大值取的是largest_number/2,作为被减数，让它小一点。
    b_int = np.random.randint(largest_number/2) 
    #如果生成的b大了，那么交换一下
    if a_int<b_int:
        tt = a_int
        b_int = a_int
        a_int=tt
    
    a = int2binary[a_int] # binary encoding
    b = int2binary[b_int] # binary encoding    
    # true answer
    c_int = a_int - b_int
    c = int2binary[c_int]
    
    # 存储神经网络的预测值
    d = np.zeros_like(c)
    overallError = 0 #每次把总误差清零
    
    layer_2_deltas = list() #存储每个时间点输出层的误差
    layer_1_values = list() #存储每个时间点隐藏层的值
    
    layer_1_values.append(np.ones(hidden_dim)*0.1) # 一开始没有隐藏层，所以初始化一下原始值为0.1
    
    # moving along the positions in the binary encoding
    for position in range(binary_dim):#循环遍历每一个二进制位
        
        # generate input and output
        X = np.array([[a[binary_dim - position - 1],b[binary_dim - position - 1]]])#从右到左，每次去两个输入数字的一个bit位
        y = np.array([[c[binary_dim - position - 1]]]).T#正确答案
        # hidden layer (input ~+ prev_hidden)
        layer_1 = sigmoid(np.dot(X,synapse_0) + np.dot(layer_1_values[-1],synapse_h))#（输入层 + 之前的隐藏层） -> 新的隐藏层，这是体现循环神经网络的最核心的地方！！！
        # output layer (new binary representation)
        layer_2 = sigmoid(np.dot(layer_1,synapse_1)) #隐藏层 * 隐藏层到输出层的转化矩阵synapse_1 -> 输出层
        
        layer_2_error = y - layer_2 #预测误差
        layer_2_deltas.append((layer_2_error)*sigmoid_output_to_derivative(layer_2)) #把每一个时间点的误差导数都记录下来
        overallError += np.abs(layer_2_error[0])#总误差
    
        d[binary_dim - position - 1] = np.round(layer_2[0][0]) #记录下每一个预测bit位
        
        # store hidden layer so we can use it in the next timestep
        layer_1_values.append(copy.deepcopy(layer_1))#记录下隐藏层的值，在下一个时间点用
    
    future_layer_1_delta = np.zeros(hidden_dim)
    
    #反向传播，从最后一个时间点到第一个时间点
    for position in range(binary_dim):
        
        X = np.array([[a[position],b[position]]]) #最后一次的两个输入
        layer_1 = layer_1_values[-position-1] #当前时间点的隐藏层
        prev_layer_1 = layer_1_values[-position-2] #前一个时间点的隐藏层
        
        # error at output layer
        layer_2_delta = layer_2_deltas[-position-1] #当前时间点输出层导数
        # error at hidden layer
        # 通过后一个时间点（因为是反向传播）的隐藏层误差和当前时间点的输出层误差，计算当前时间点的隐藏层误差
        layer_1_delta = (future_layer_1_delta.dot(synapse_h.T) + layer_2_delta.dot(synapse_1.T)) * sigmoid_output_to_derivative(layer_1)
        
        
       # 等到完成了所有反向传播误差计算， 才会更新权重矩阵，先暂时把更新矩阵存起来。
        synapse_1_update += np.atleast_2d(layer_1).T.dot(layer_2_delta)
        synapse_h_update += np.atleast_2d(prev_layer_1).T.dot(layer_1_delta)
        synapse_0_update += X.T.dot(layer_1_delta)
        
        future_layer_1_delta = layer_1_delta
    
    # 完成所有反向传播之后，更新权重矩阵。并把矩阵变量清零
    synapse_0 += synapse_0_update * alpha
    synapse_1 += synapse_1_update * alpha
    synapse_h += synapse_h_update * alpha
    synapse_0_update *= 0
    synapse_1_update *= 0
    synapse_h_update *= 0
   
    # print out progress
    if(j % 800 == 0):
        #print(synapse_0,synapse_h,synapse_1)
        print("总误差:" + str(overallError))
        print("Pred:" + str(d))
        print("True:" + str(c))
        out = 0
        for index,x in enumerate(reversed(d)):
            out += x*pow(2,index)
        print(str(a_int) + " - " + str(b_int) + " = " + str(out))
        print("------------")

常见的循环神经网络单元及结构

上述实例仅限于简单的逻辑和样本，对于相对复杂的问题有缺陷，原因在激活函数上。
通常像Sigmoid、tanh这类激活函数在神经网络里最多只能有6层左右，因为反向误差的传播会导致随着层数增加传递的误差值越小。RNN中，误差传递不光在层之间，还在每层的样本序列之间，因此其无法学习太长的序列特征。
在深层网络结构中，会将简单的RNN模型从两个角度进行改造：
1.使用结构更复杂的RNN模型的基本单元，使其在单层网络上提取更好的记忆特征。
2.将多个基本单元结合起来，组成不同的结构（多层RNN，双向RNN等），有时还会配合全连接网络、卷积网络等多种模型结构，一起组成拟合能力更强的网络模型。

长短记忆（LSTM）单元

一种使用了类似搭桥术结构的RNN单元，可以学习长期序列信息，是RNN网络中最常用的Cell之一。
看起来比较复杂其实是一个带有tanh激活函数的简单RNN，原理是引入一个成为细胞状态的连接，用来存放想要记忆的东西，（对应于简单RNN中的h，只不过不再只是保存上一次的状态了，而是通过网络学习存放那些有用的状态），同时在里面加入3个门，忘记门、输入门、输出门。

门控制循环单元（GRU）

几乎是与LSTM功能一样的常用网络结构，它将忘记门和输入门合成了一个单一的更新门，同时又将细胞状态和隐藏状态进行混合，以及一些其他的改动，最终的模型比LSTM模型要简单，少一个状态输出，但效果几乎一样，可以让代码更简单。

只有忘记门的LSTM（JANET）单元

只有忘记门时，性能居然优于标志LSTM，该优化方式也可以用在GRU。

独立循环单元（IndRNN）单元

效果和速度都优于LSTM单元，不但能解决传统RNN模型存在的梯度消失和梯度爆炸问题，而且可以更好学习样本中长期依赖的关系。
在搭建模型时：
可以用堆叠、残差、全连接的方式使用IndRNN单元，搭建更深的网络结构；
将IndRNN单元配合ReLU等非饱和激活函数一起使用，会使模型表现出很好的鲁棒性。

IndRNN与LSTM单元相比，使用了更简单的结构，比其快10倍，更像一个原始的RNN模型结构（只将神经元的输出复制到节点之中），其在循环层部分做了特殊处理。
通过公式来详细介绍…

双向RNN结构

又称Bi-RNN，采用了两个方向的RNN模型。正反结合比单向的循环网络有更高的拟合度。例如预测一个语句中缺失的词语，需要根据上下文来预测。
略…

实例11：用循环神经网络训练语言模型

还涉及自然语言处理（NLP）领域的相关知识，语言模型包括文法语言模型和统计语言模型，一般指统计语言模型。略…只做了解。
PyTorch中，有两个封装好的RNN类，LSTM和GRU。
解码要改成utf-8
labels =labels+label.decode(‘utf-8’)

import torch
import torch.nn.functional as F
import time
import random
import numpy as np
from collections import Counter

import sys

# print(sys.getdefaultencoding()) 

RANDOM_SEED = 123
torch.manual_seed(RANDOM_SEED)

DEVICE = torch.device('cuda' if torch.cuda.is_available() else 'cpu')



def elapsed(sec):
    if sec<60:
        return str(sec) + " sec"
    elif sec<(60*60):
        return str(sec/60) + " min"
    else:
        return str(sec/(60*60)) + " hr"


training_file = 'wordstest.txt'


#中文多文件
def readalltxt(txt_files):
    labels = []
    for txt_file in txt_files:
        
        target = get_ch_lable(txt_file)
        labels.append(target)  
    return labels
    
#中文字
def get_ch_lable(txt_file):  
    labels= ""
    with open(txt_file, 'rb') as f:
        for label in f: 
            #labels =label.decode('utf-8')
            labels =labels+label.decode('utf-8')
           
    return  labels
    


#优先转文件里的字符到向量
def get_ch_lable_v(txt_file,word_num_map,txt_label=None):
      
    words_size = len(word_num_map)   
    to_num = lambda word: word_num_map.get(word, words_size) 
    if txt_file!= None:
        txt_label = get_ch_lable(txt_file)

    labels_vector = list(map(to_num, txt_label)) 
    return labels_vector  
    
training_data =get_ch_lable(training_file)

print("Loaded training data...")

print('样本长度:',len(training_data))
counter = Counter(training_data)  
words = sorted(counter)
words_size= len(words)
word_num_map = dict(zip(words, range(words_size))) 

print('字表大小:', words_size)     
wordlabel = get_ch_lable_v(training_file,word_num_map)

class GRURNN(torch.nn.Module):
    def __init__(self, word_size, embed_dim,
                 hidden_dim, output_size, num_layers):
        super(GRURNN, self).__init__()

        self.num_layers = num_layers
        self.hidden_dim = hidden_dim
        
        self.embed = torch.nn.Embedding(word_size, embed_dim)
        self.gru = torch.nn.GRU(input_size=embed_dim,
                                hidden_size=hidden_dim,
                                num_layers=num_layers,bidirectional=True)
        self.fc = torch.nn.Linear(hidden_dim*2, output_size)

    
    def forward(self, features, hidden):
        embedded = self.embed(features.view(1, -1))
        output, hidden = self.gru(embedded.view(1, 1, -1), hidden)
        output = self.fc(output.view(1, -1))
        return output, hidden
      
    def init_zero_state(self):
        init_hidden = torch.zeros(self.num_layers*2, 1, self.hidden_dim).to(DEVICE)
        return init_hidden



EMBEDDING_DIM = 10
HIDDEN_DIM = 20
NUM_LAYERS = 1

model = GRURNN(words_size, EMBEDDING_DIM, HIDDEN_DIM, words_size, NUM_LAYERS)
model = model.to(DEVICE)
optimizer = torch.optim.Adam(model.parameters(), lr=0.005)


def evaluate(model, prime_str, predict_len, temperature=0.8):

    hidden = model.init_zero_state().to(DEVICE)
    predicted = ''

    #处理输入语义
    for p in range(len(prime_str) - 1):
        _, hidden = model(prime_str[p], hidden)
        predicted +=words[prime_str[p]]
    inp = prime_str[-1]
    predicted +=words[inp]
    
    for p in range(predict_len):
        output, hidden = model(inp, hidden)
        
        #从多项式分布中采样
        output_dist = output.data.view(-1).div(temperature).exp()
        inp = torch.multinomial(output_dist, 1)[0]
        
        predicted += words[inp]

    return predicted


#定义参数训练模型
training_iters = 5000
display_step = 1000
n_input = 4
step = 0
offset = random.randint(0,n_input+1)
end_offset = n_input + 1

while step < training_iters:
    start_time = time.time()

    # 随机取一个位置偏移
    if offset > (len(training_data)-end_offset):
        offset = random.randint(0, n_input+1)
   

    inwords =wordlabel[offset:offset+n_input]
    inwords = np.reshape(np.array(inwords), [n_input, -1,  1])

    out_onehot = wordlabel[offset+1:offset+n_input+1]


    hidden = model.init_zero_state()
    optimizer.zero_grad()
    
    loss = 0.
    inputs, targets = torch.LongTensor(inwords).to(DEVICE), torch.LongTensor(out_onehot).to(DEVICE)
    for c in range(n_input):

        outputs, hidden = model(inputs[c], hidden)
        loss += F.cross_entropy(outputs, targets[c].view(1))

    loss /= n_input
    loss.backward()

    optimizer.step()

    #输出日志
    with torch.set_grad_enabled(False):
        if (step+1) % display_step == 0:
            print(f'Time elapsed: {(time.time() - start_time)/60:.4f} min')
            print(f'step {step+1} | Loss {loss.item():.2f}\n\n')
            with torch.no_grad():
                print(evaluate(model, inputs, 32), '\n')
            print(50*'=')

    step += 1
    offset += (n_input+1)#中间隔了一个，作为预测

print("Finished!")

while True:
    prompt = "请输入几个字，最好是%s个: " % n_input
    sentence = input(prompt)
    inputword = sentence.strip()
    
    try:
        inputword = get_ch_lable_v(None,word_num_map,inputword)
        keys = np.reshape(np.array(inputword), [ len(inputword),-1, 1])
        model.eval()
        with torch.no_grad():
            sentence =evaluate(model, torch.LongTensor(keys).to(DEVICE), 32)

        print(sentence)
    except:
        print("该字我还没学会")

过拟合问题及优化技巧

介绍一下神经网络在训练过程中的一些常用技巧。

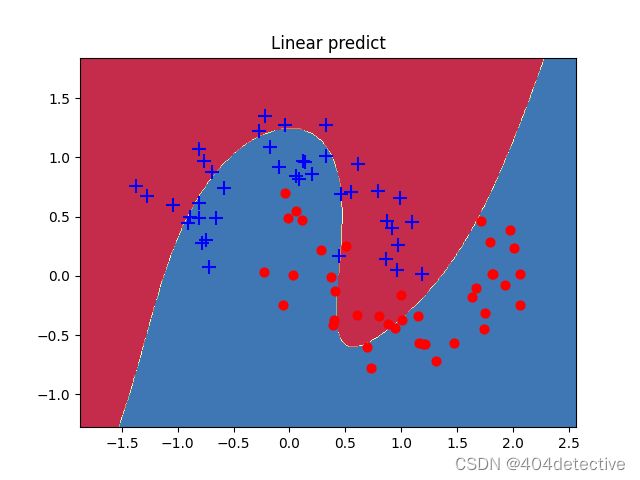
实例12：训练具有过拟合问题的模型

可以用下面引用其他写的example1.py，不知道为什么会运行一遍原来文件的函数。
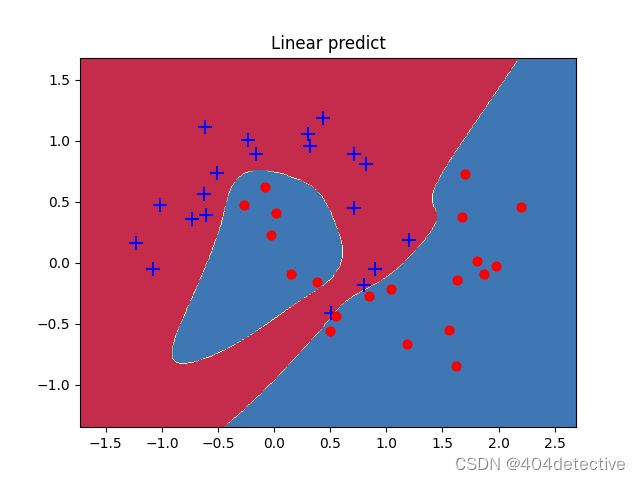
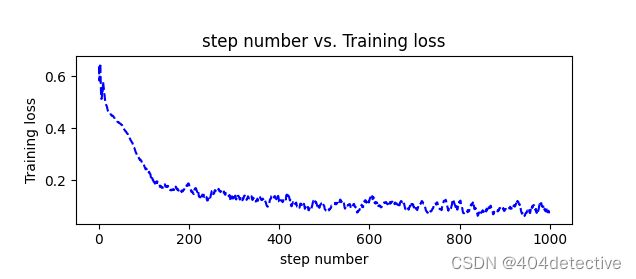
可以看图看出过拟合。

import sys
sys.path.append('pytorch\chapter3')
from example1 import LogicNet,moving_average,predict,plot_decision_boundary

import sklearn.datasets     #引入数据集
import torch
import numpy as np
import matplotlib.pyplot as plt
import sys
sys.path.append('pytorch\chapter3')
from example1 import LogicNet,moving_average,predict,plot_decision_boundary

np.random.seed(0)           #设置随机数种子
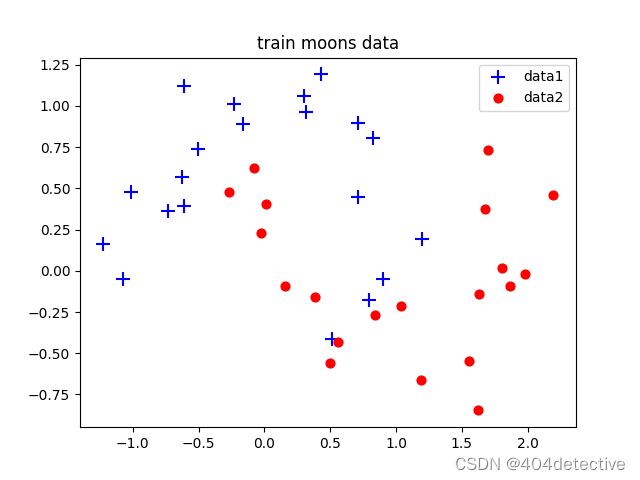
X, Y = sklearn.datasets.make_moons(40,noise=0.2) #生成2组半圆形数据

arg = np.squeeze(np.argwhere(Y==0),axis = 1)     #获取第1组数据索引
arg2 = np.squeeze(np.argwhere(Y==1),axis = 1)#获取第2组数据索引

plt.title("train moons data")
plt.scatter(X[arg,0], X[arg,1], s=100,c='b',marker='+',label='data1')
plt.scatter(X[arg2,0], X[arg2,1],s=40, c='r',marker='o',label='data2')
plt.legend()
plt.show()


model = LogicNet(inputdim=2,hiddendim=500,outputdim=2)#初始化模型
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)#定义优化器


xt = torch.from_numpy(X).type(torch.FloatTensor)#将Numpy数据转化为张量
yt = torch.from_numpy(Y).type(torch.LongTensor)
epochs = 1000#定义迭代次数
losses = []#定义列表，用于接收每一步的损失值
for i in range(epochs):
    loss = model.getloss(xt,yt)
    losses.append(loss.item())
    optimizer.zero_grad()#清空之前的梯度
    loss.backward()#反向传播损失值
    optimizer.step()#更新参数


avgloss= moving_average(losses) #获得损失值的移动平均值
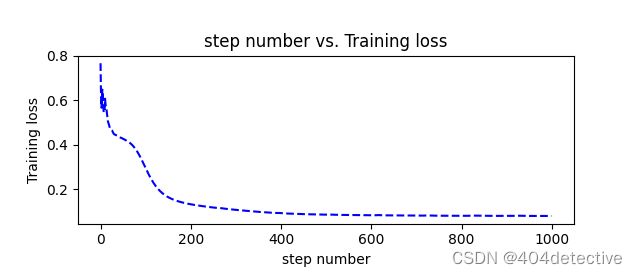
plt.figure(1)
plt.subplot(211)
plt.plot(range(len(avgloss)), avgloss, 'b--')
plt.xlabel('step number')
plt.ylabel('Training loss')
plt.title('step number vs. Training loss')
plt.show()


plot_decision_boundary(lambda x : predict(model,x) ,X, Y)
from sklearn.metrics import accuracy_score
print("训练时的准确率：",accuracy_score(model.predict(xt),yt))

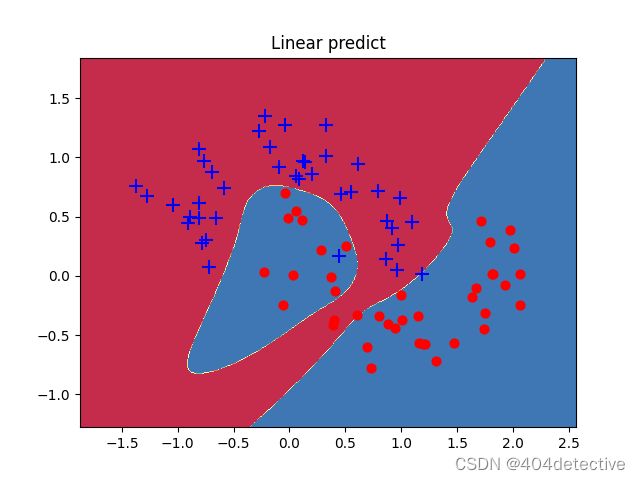
Xtest, Ytest = sklearn.datasets.make_moons(80,noise=0.2) #生成2组半圆形数据
plot_decision_boundary(lambda x : predict(model,x) ,Xtest, Ytest)
Xtest_t = torch.from_numpy(Xtest).type(torch.FloatTensor)#将Numpy数据转化为张量
Ytest_t = torch.from_numpy(Ytest).type(torch.LongTensor)
print("测试时的准确率：",accuracy_score(model.predict(Xtest_t),Ytest_t))

训练时的准确率： 1.0

测试时的准确率： 0.9375

改善模型过拟合的方法

如early stopping、数据集扩增、正则化、Dropout。
early stopping：在数据过拟合之前结束，不好把控。
数据集扩增：让模型看到更多的情况，最大化满足全样本，但在实际中为未来事件预测力不从心。
正则化：通过引入范数概念，增强泛化能力，有L1正则化、L2正则化。
Dropout：每次训练舍去一些节点来增强泛化能力

了解正则化

所谓正则化，就是在神经网络计算损失过程中，在损失后面加一项来干扰，实现模型无法和与样本完全拟合，从而抑制过拟合。

正则化的分类和公式

干扰项一定要有以下特征
当欠拟合时，希望它对模型误差影响尽量小，让模型快速拟合实际。
过拟合时，希望影响大，让模型不要产生过拟合的情况。
于是引入了两个范数——L1、L2
L1：所有学习参数的w的绝对值的和
L2：所有学习参数的w的平方和，然后求平方根
实际应用中L2最常用

L2正则化的实现

直接的方式是用优化器自带的weight_decay参数指定权重值衰减率，相当于L2正则化中的λ。默认对w和b都处理，实际上只需要对w，如果对b可能会欠拟合。

实例13：用L2正则改善模型的过拟合情况

在实例12上添加正则化处理，重新进行训练。

#添加正则化处理
weight_p, bias_p = [],[]
for name, p in model.named_parameters():
    if 'bias' in name:
        bias_p += [p]
    else:
        weight_p += [p]
optimizer = torch.optim.Adam([{'params': weight_p, 'weight_decay':0.001},
                      {'params': bias_p, 'weight_decay':0}],
                      lr=0.01)

训练时的准确率由1到0.975，是由于L2正则化干扰项
测试时的准确率由0.9375到0.9875，表明L2改善了过拟合

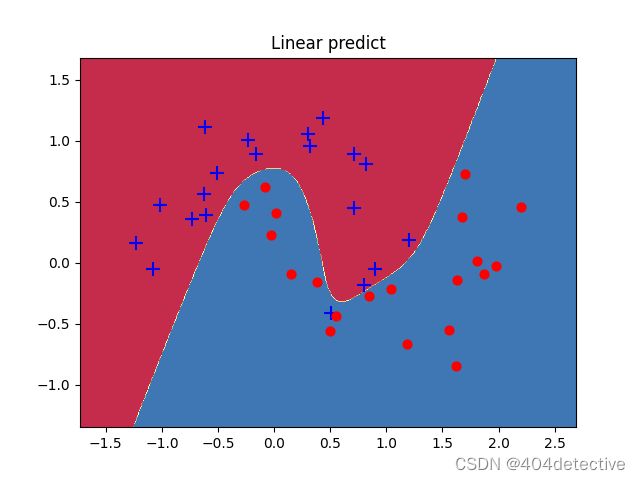
观察训练和测试图片没有了闭合区间，更接近原始的数据分布。

实例14：通过增大数据集改善模型的过拟合状况

不再生成一次，而是循环生成40次，修改每次训练都加入新的数据集。
在迭代中加入

    X, Y = sklearn.datasets.make_moons(40,noise=0.2) #生成2组半圆形数据
    xt = torch.from_numpy(X).type(torch.FloatTensor)#将Numpy数据转化为张量
    yt = torch.from_numpy(Y).type(torch.LongTensor)

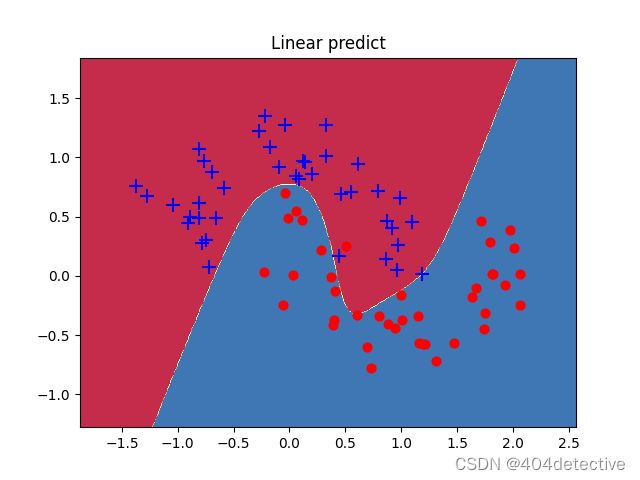
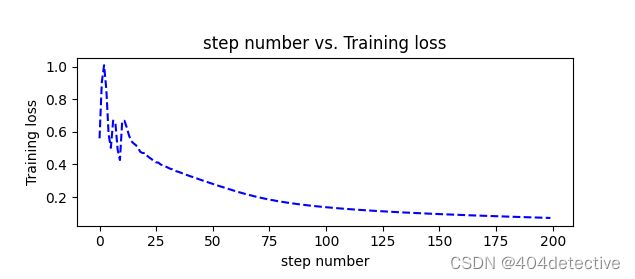
可以看出loss曲线有明显的抖动，是由于新数据对上一次模型的拟合能力冲突较大，经过多次迭代就可以不断修正错误，达到合理的拟合能力。

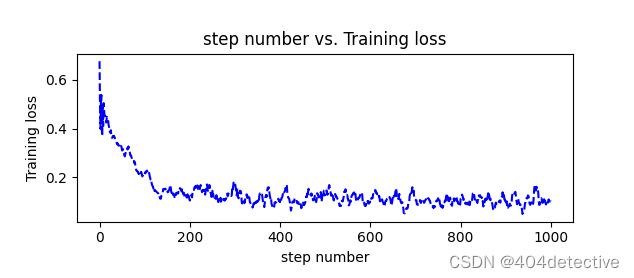
与之前对比
训练时的准确率由1到0.95，是由于训练了新的数据
测试时的准确率由0.9375到0.975，表明增大数据集的方法改进了过拟合情况。


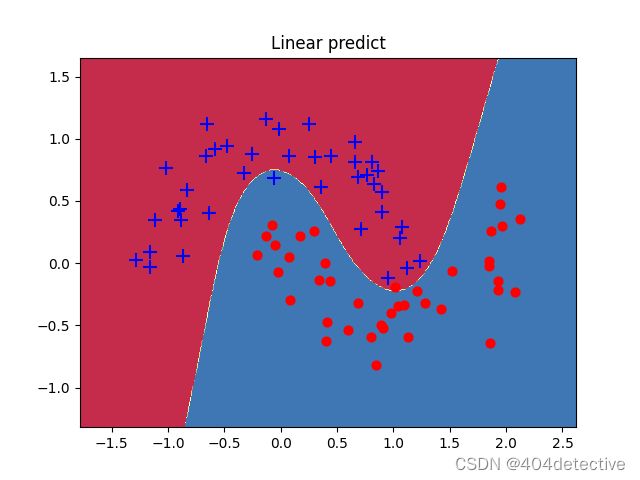
观察图片没有了闭合区间，更接近原始的数据分布。

Dropout方法

原理：每次随机选择一部分节点不去学习，是因为过拟合是把一些异常数据当成规律来学习，但其量非常少，利用上述特性，每次训练忽略一些节点，将小概率的异常数据获得学习的机会变得更低。但不是丢弃越多越好，会降低拟合速度。它改变了网络结构，只能训练的时候用，测试时候要改成False。使用类的方式时候，没有training参数，因为它会根据调用方式自己调节。

实例15：通过Dropout方法改善模型的过拟合状况

为了简化代码，之间继承模型类，然后重写前向结构。

#继承LogicNet类，构建网络模型
class Logic_Dropout_Net(LogicNet):
    def __init__(self,inputdim,hiddendim,outputdim):#初始化网络结构
        super(Logic_Dropout_Net,self).__init__(inputdim,hiddendim,outputdim)

    def forward(self,x): #搭建用两层全连接组成的网络模型
        x = self.Linear1(x)#将输入数据传入第1层
        x = torch.tanh(x)#对第一层的结果进行非线性变换
        x = nn.functional.dropout(x, p=0.07, training=self.training)
        x = self.Linear2(x)#再将数据传入第2层
        return x

与之前对比
训练时的准确率由1到0.925
测试时的准确率由0.9375到0.95
测试准确率同样没有低于训练准确率，说明Dropout方式有效改善过拟合

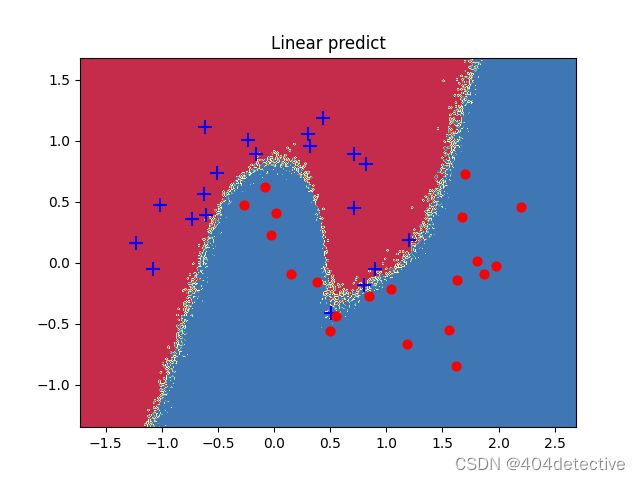
观察图片没有了闭合区间，更接近原始的数据分布。

全连接网络的深浅与泛化能力的联系

浅层网络有更好的拟合能力，但泛化能力弱，深层反之。
实际过程要考虑二者平衡，如wide_deep模型，就是单层线性模型（浅层全连接网络模型）和深度的全连接模型（深层全连接网络模型）。

了解批量归一化（BN）算法

一般用在全连接神经网络和卷积神经网络中，它的问世让整个神经网络的识别准确率上升了一个台阶。
权重值差太大，会让网络无法计算产生梯度爆炸，原因是网络内部协变量的转移，即正向传播时的不同层的参数会将反向训练计算时所参照的数据样本分布改变。
引入批量归一化的作用：最大限度的保证每次正向传播输出在同一分布上，这样反向计算时参照的数据样本分布就会与正向一样了。保证了分布统一，对权重的调整才会更有意义。
算法实现就是将每一层运算出来的数据归一化成均值为0、方差为1的标准高斯分布，这样就会在保留样本的分布特征的同时，又消除了层与层之间的分布差异。实际上加两个参数通过训练获得。

实例16：手动实现批量归一化的计算方法

data为2个样本，2个通道高宽为2和1。
BatchNorm2d接口为数据的每个通道创建一套自适应参数，实际计算中根据每个通道的数据进行批量归一化计算的。
经过批量归一化后，只改变了值没有改变形状。
最后手动计算第1通道中第一个数据的BN，结果与接口一致。

import torch
import torch.nn as nn
data=torch.randn(2,2,2,1)
print(data)
tensor([[[[-0.3322],  
          [ 0.2331]], 

         [[ 0.0162],  
          [ 1.0788]]],


        [[[ 0.6592],
          [ 1.3542]],

         [[-0.0912],
          [ 0.9763]]]])
obn=nn.BatchNorm2d(2,affine=True) #实例化自适应BN对象
output=obn(data)
print(obn.weight)
print(obn.bias)
print(obn.eps)
print(output,output.size())
#自适应参数
Parameter containing:
tensor([1., 1.], requires_grad=True)
Parameter containing:
tensor([0., 0.], requires_grad=True)
1e-05
tensor([[[[-1.3166],
          [-0.3986]],

         [[-0.8948],
          [ 1.0910]]],


        [[[ 0.2933],
          [ 1.4218]],

         [[-1.0955],
          [ 0.8994]]]], grad_fn=<NativeBatchNormBackward0>) torch.Size([2, 2, 2, 1])

print("第1通道的数据:",data[:,0])
 
#计算第1通道数据的均值和方差
Mean=torch.Tensor.mean(data[:,0])
Var=torch.Tensor.var(data[:,0],False)   #false表示贝塞尔校正不会被使用
print(Mean)
print(Var)

#计算第1通道中第一个数据的BN
batchnorm=((data[0][0][0][0]-Mean)/(torch.pow(Var,0.5)+obn.eps))\
    *obn.weight[0]+obn.bias[0]
print(batchnorm)
第1通道的数据: tensor([[[-0.3322],
         [ 0.2331]],

        [[ 0.6592],
         [ 1.3542]]])
tensor(0.4786)
tensor(0.3793)
tensor(-1.3166, grad_fn=<AddBackward0>)

实例17：通过批量归一化方法改善模型形状

继承模型后进行BN处理

#继承LogicNet类，构建网络模型
class Logic_BN_Net(LogicNet):
    def __init__(self,inputdim,hiddendim,outputdim):#初始化网络结构
        super(Logic_BN_Net,self).__init__(inputdim,hiddendim,outputdim)
        self.BN = nn.BatchNorm1d(hiddendim) #定义BN层
    def forward(self,x): #搭建用两层全连接组成的网络模型
        x = self.Linear1(x)#将输入数据传入第1层
        x = torch.tanh(x)#对第一层的结果进行非线性变换
        x = self.BN(x)#将第一层的数据做BN处理
        x = self.Linear2(x)#再将数据传入第2层
        return x

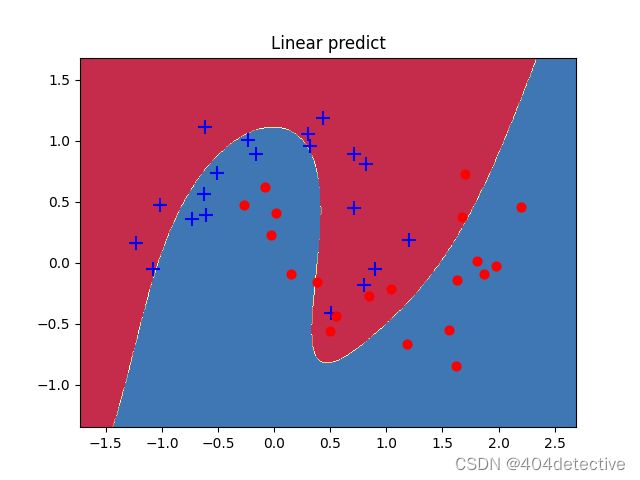
与之前对比
训练时的准确率由1到0.975
测试时的准确率由0.9375到0.925
说明BN有效改善过拟合

注意力机制

让神经网络忽略不重要的特征向量，重点计算有用的，抛弃无用特征对拟合效果的干扰同时能提高运算速度。
通过注意力分数来实现，是一个0到1的值，可以用在任何网络中。
可以作用在RNN模型中的每个序列上，在模型输出的特征向量上。
有两种模式，软模式（所有数据都注意）、硬模式（会舍弃一部分不符合条件的注意力权值为0）。
多头注意力机制…自注意力机制…

实例18：利用注意力循环神经网络对图片分类

import torchvision
import torchvision.transforms as tranforms
data_dir = './fashion_mnist/'
tranform = tranforms.Compose([tranforms.ToTensor()])
train_dataset = torchvision.datasets.FashionMNIST(data_dir, train=True, transform=tranform,download=True)

print("训练数据集条数",len(train_dataset))
val_dataset  = torchvision.datasets.FashionMNIST(root=data_dir, train=False, transform=tranform)
print("测试数据集条数",len(val_dataset))
import pylab
im = train_dataset[0][0]
im = im.reshape(-1,28)
pylab.imshow(im)
pylab.show()
print("该图片的标签为：",train_dataset[0][1])

############数据集的制作
import torch
batch_size = 10
train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
test_loader = torch.utils.data.DataLoader(val_dataset, batch_size=batch_size, shuffle=False)


from matplotlib import pyplot as plt
import numpy as np
def imshow(img):
    print("图片形状：",np.shape(img))
    npimg = img.numpy()
    plt.axis('off')
    plt.imshow(np.transpose(npimg, (1, 2, 0)))

classes = ('T-shirt', 'Trouser', 'Pullover', 'Dress', 'Coat', 'Sandal', 'Shirt', 'Sneaker', 'Bag', 'Ankle_Boot')
sample = iter(train_loader)
images, labels = sample.next()
print('样本形状：',np.shape(images))
print('样本标签：',labels)
imshow(torchvision.utils.make_grid(images,nrow=batch_size))
print(','.join('%5s' % classes[labels[j]] for j in range(len(images))))

############


#########################################################################################################################



#定义myLSTMNet模型类，该模型包括 2个RNN层和1个全连接层
class myLSTMNet(torch.nn.Module):
    def __init__(self,in_dim, hidden_dim, n_layer, n_class):
        super(myLSTMNet, self).__init__()
        #定义循环神经网络层
        self.lstm = torch.nn.LSTM(in_dim, hidden_dim, n_layer,batch_first=True)
        self.Linear = torch.nn.Linear(hidden_dim*28, n_class)#定义全连接层
        self.attention = AttentionSeq(hidden_dim,hard=0.03)

    def forward(self, t):    #搭建正向结构
        t, _ = self.lstm(t)  #进行RNN处理
        t = self.attention(t)
        t=t.reshape(t.shape[0],-1)
#        t = t[:, -1, :]      #获取RNN网络的最后一个序列数据
        out = self.Linear(t) #进行全连接处理
        return out
class AttentionSeq(torch.nn.Module):

    def __init__(self, hidden_dim,hard= 0):
        super(AttentionSeq, self).__init__()
        self.hidden_dim = hidden_dim
        self.dense = torch.nn.Linear(hidden_dim, hidden_dim)
        self.hard = hard

    def forward(self, features, mean=False):
        #[batch,seq,dim]
        batch_size, time_step, hidden_dim = features.size()
        weight = torch.nn.Tanh()(self.dense(features))

        # mask给负无穷使得权重为0
        mask_idx = torch.sign(torch.abs(features).sum(dim=-1))
#        mask_idx = mask_idx.unsqueeze(-1).expand(batch_size, time_step, hidden_dim)
        mask_idx = mask_idx.unsqueeze(-1).repeat(1, 1, hidden_dim)


        weight = torch.where(mask_idx== 1, weight,
                             torch.full_like(mask_idx,(-2 ** 32 + 1)))
        weight = weight.transpose(2, 1)
        weight = torch.nn.Softmax(dim=2)(weight)
        if self.hard!=0: #hard mode
            weight = torch.where(weight>self.hard, weight, torch.full_like(weight,0))
        
        if mean:
            weight = weight.mean(dim=1)
            weight = weight.unsqueeze(1)
            weight = weight.repeat(1, hidden_dim, 1)
        weight = weight.transpose(2, 1)
        features_attention = weight * features

        return features_attention
#实例化模型对象
network = myLSTMNet(28, 128, 2, 10)  # 图片大小是28x28
#指定设备
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
print(device)
network.to(device)
print(network)#打印网络

criterion = torch.nn.CrossEntropyLoss()  #实例化损失函数类
optimizer = torch.optim.Adam(network.parameters(), lr=.01)

for epoch in range(2): #数据集迭代2次
    running_loss = 0.0
    for i, data in enumerate(train_loader, 0): #循环取出批次数据
        inputs, labels = data
        inputs = inputs.squeeze(1)
        inputs, labels = inputs.to(device), labels.to(device) #
        optimizer.zero_grad()#清空之前的梯度
        outputs = network(inputs)
        loss = criterion(outputs, labels)#计算损失
        loss.backward()  #反向传播
        optimizer.step() #更新参数

        running_loss += loss.item()
        if i % 1000 == 999:
            print('[%d, %5d] loss: %.3f' %
                (epoch + 1, i + 1, running_loss / 2000))
            running_loss = 0.0




print('Finished Training')


#使用模型
dataiter = iter(test_loader)
images, labels = dataiter.next()

inputs, labels = images.to(device), labels.to(device)


imshow(torchvision.utils.make_grid(images,nrow=batch_size))
print('真实标签: ', ' '.join('%5s' % classes[labels[j]] for j in range(len(images))))
inputs = inputs.squeeze(1)
outputs = network(inputs)
_, predicted = torch.max(outputs, 1)


print('预测结果: ', ' '.join('%5s' % classes[predicted[j]]
                              for j in range(len(images))))


#测试模型
class_correct = list(0. for i in range(10))
class_total = list(0. for i in range(10))
with torch.no_grad():
    for data in test_loader:
        images, labels = data
        images = images.squeeze(1)
        inputs, labels = images.to(device), labels.to(device)
        outputs = network(inputs)
        _, predicted = torch.max(outputs, 1)
        predicted = predicted.to(device)
        c = (predicted == labels).squeeze()
        for i in range(10):
            label = labels[i]
            class_correct[label] += c[i].item()
            class_total[label] += 1


sumacc = 0
for i in range(10):
    Accuracy = 100 * class_correct[i] / class_total[i]
    print('Accuracy of %5s : %2d %%' % (classes[i], Accuracy ))
    sumacc =sumacc+Accuracy
print('Accuracy of all : %2d %%' % ( sumacc/10. ))

输出结果如下：
训练数据集条数 60000
测试数据集条数 10000
libpng warning: iCCP: cHRM chunk does not match sRGB
该图片的标签为： 9
样本形状： torch.Size([10, 1, 28, 28])
样本标签： tensor([2, 2, 5, 3, 7, 1, 7, 9, 2, 9])
图片形状： torch.Size([3, 32, 302])
Pullover,Pullover,Sandal,Dress,Sneaker,Trouser,Sneaker,Ankle_Boot,Pullover,Ankle_Boot
cpu
myLSTMNet(
(lstm): LSTM(28, 128, num_layers=2, batch_first=True)
(Linear): Linear(in_features=3584, out_features=10, bias=True)
(attention): AttentionSeq(
(dense): Linear(in_features=128, out_features=128, bias=True)
)
)
[1, 1000] loss: 0.381
[1, 2000] loss: 0.261
[1, 3000] loss: 0.240
[1, 4000] loss: 0.216
[1, 5000] loss: 0.205
[1, 6000] loss: 0.207
[2, 1000] loss: 0.231
[2, 2000] loss: 0.281
[2, 3000] loss: 0.282
[2, 4000] loss: 0.265
[2, 5000] loss: 0.238
[2, 6000] loss: 0.230
Finished Training
图片形状： torch.Size([3, 32, 302])
真实标签: Ankle_Boot Pullover Trouser Trouser Shirt Trouser Coat Shirt Sandal Sneaker
预测结果: Ankle_Boot Pullover Trouser Trouser Shirt Trouser Pullover Shirt Sandal Sneaker
Accuracy of T-shirt : 78 %
Accuracy of Trouser : 95 %
Accuracy of Pullover : 81 %
Accuracy of Dress : 75 %
Accuracy of Coat : 65 %
Accuracy of Sandal : 89 %
Accuracy of Shirt : 54 %
Accuracy of Sneaker : 91 %
Accuracy of Bag : 95 %
Accuracy of Ankle_Boot : 95 %
Accuracy of all : 82 %

这一章内容也太多了，都有点烦了。。。