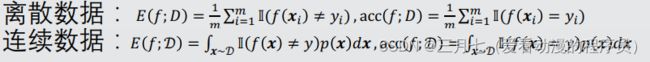机器学习---经验误差与过拟合、方差与偏差、性能度量、比较检验
1. 经验误差与过拟合
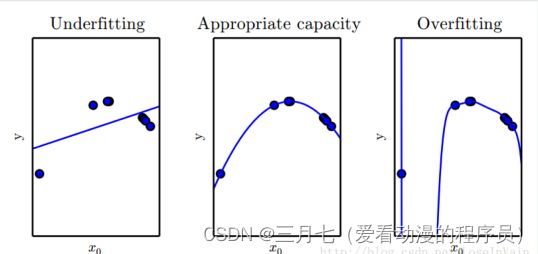
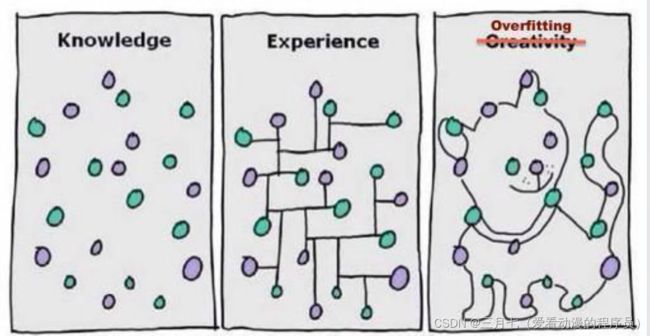
第三张图建立的模型,在训练集中通过x可以很好的预测y,然而我们不能预期该模型能够很好的预
测集外的数据,换句话说,这个模型没有很好的泛化能力。
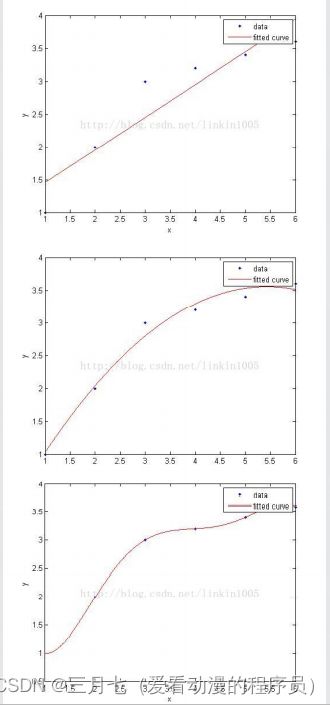
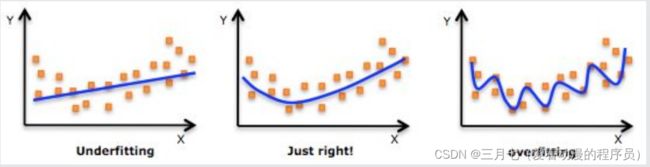
第一张图建立了一个线性模型,但是该模型并没有精确地捕捉到训练集数据的结构,我们称具有第
一张图较大的偏倚(bias),也称欠拟合。
第三张图通过5次多项式函数很好的对样本进行了拟合,然而,如果将建立的模型进行泛化,并不
能很好的对训练集之外的数据进行预测,也称过拟合。
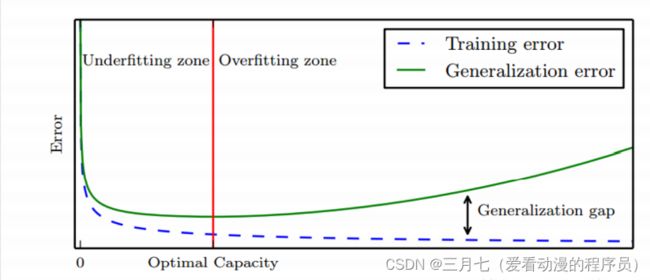
机器学习的主要挑战在于在未见过的数据输入上表现良好,这个能力称为泛化能力
(generalization)。
误差:学习器实际预测输出与样本真实输出的差异。
训练集误差:训练误差
训练集的补集:泛化误差
测试集误差:测试误差
我们希望得到泛化误差小的学习器。
过拟合:训练过度使泛化能力下降。
欠拟合:未能学好训练样本的普遍规律。
过拟合是机器学习的关键障碍,且不可避免。
模型误差包含了数据误差,或者说模型信息中包含了噪声。
过拟合的例子:比如在考试之前,有人采取题海战术,把每个题目都背下来,但是题目变化就答
不上来,因为这种方法并没有抽象出一般的规则。
训练集S和测试集T组成数据集D。
假设测试样本是从真实分布中采样而得,避免因数据划分引入偏差。
测试集应与训练集互斥。
学习器泛化评估的测试方法:
2. 方差与偏差
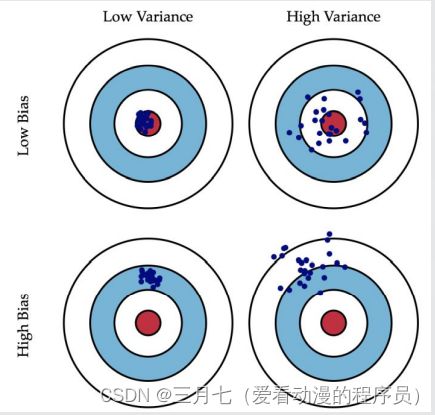
想象你开着一架直升机,攻击地面上一只敌军部队,于是你连打数十梭子,结果有一下几种情况:
1. 子弹基本上都打在队伍经过的一棵树上了,这就是方差小(子弹打得很集中),偏差大(跟目的
相距甚远)。
2. 子弹打在了树上,石头上,花花草草也都中弹,但是敌军安然无恙,这就是方差大(子弹到处都
是),偏差大(同1)。
3. 子弹打死了一部分敌军,但是也打偏了些打到花花草草了,这就是方差大(子弹不集中),偏差
小(已经在目标周围了)。
4. 子弹一颗没浪费,每一颗都打死一个敌军,跟抗战神剧一样,这就是方差小(子弹全部都集中在
一个位置),偏差小(子弹集中的位置正是它应该射向的位置).
3. 性能度量
性能度量(performance measure):衡量模型泛化能力的评价标准。
回归:均方误差
分类:错误率和精度
混淆矩阵(confusion matrix):
查准率P与查全率R:
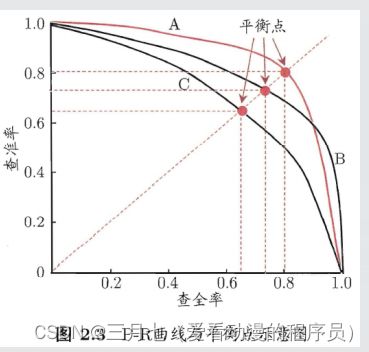
P-R曲线面积与平衡点:
ROC(受试者工作特征曲线):
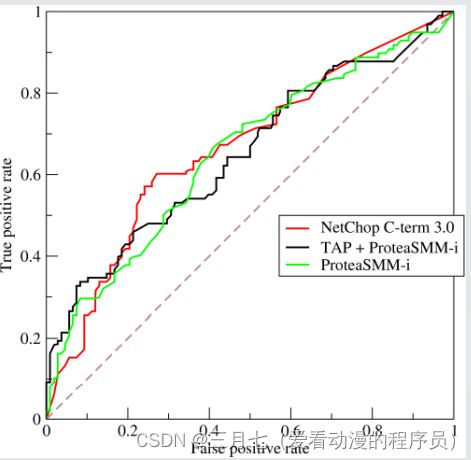
考虑ROC曲线图中的四个点和一条线。(见下图)
第一个点,(0,1),即FPR=0,TPR=1,这意味着FN(false negative) =0, 并且FP
(false positive) =0。 这是一个完美的分类器,它将所有的样本都正确分类。
第二个点,(1,0),即FPR=1,TPR=0,类似地分析可以发现这是一个最糟糕的分类器,因
为它成功避开了所有的正确答案。
第三个点,(0,0),即FPR=TPR=0,即FP(false positive)=TP (true positive)=0,可以
发现该分类 器预测所有的样本都为负样本(negative)。
第四个点(1,1),分类器实际上预测所有的样本都为正样本。
经过以上的分析,我们可以断言,ROC曲线越接近左上角,该分类器的性能越好。
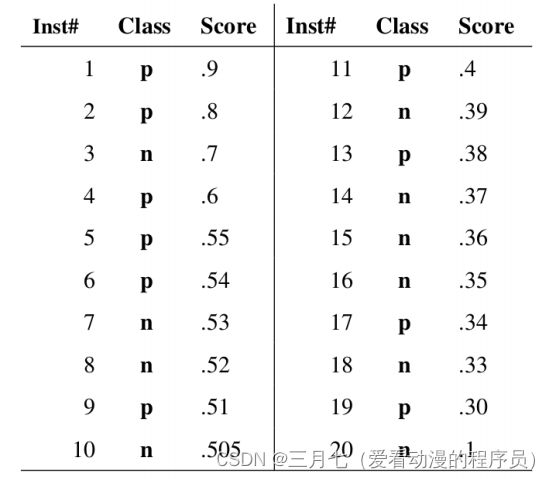
根据下图,将每个测试样本属于正样本的概率值从大到小排序。图中共有20个测试样本,“Class”
一栏表示每个测试样本真正的标签(p表示正样本,n表示负样本),“Score”表示每个测试样本属
于正样本的概率。
接下来,从高到低,依次将“Score”值作为阈值。
当测试样本属于正样本的概率大于或等于这个阈值时,我们认为它为正样本,否则为负样本。
举例来说,对于图中的第4个样本,其“Score”值为0.6,那么样本1,2,3,4都被认为是正样本,
因为它们的“Score”值都大于等于0.6,而其他样本则都认为是负样本。
每次选取一个不同的阈值,我们就可以得到一组FPR和TPR,即ROC曲线上的一点
4. 比较检验
统计假设检验(hypothesis test):根据测试错误率估计推断泛化错误率的分布。
提出假设→找到符合某种概率分布的中间变量→利用该概率分布确定在某个置信度(confidence)
下是否接受该假设。
单个学习器的情况:
做了多次留出法或者交叉验证法之后,会有多个测试误差率,此时使用”t检验“(t-test)来检验单
个学习。
根据预先设定的显著度α,以及自由度k-1,查表可得临界值b,如果Tt小于临界值b则接受,否则,
拒绝。
一个数据集多个学习器:
对一组样本D,进行k折交叉验证,会产生k个测试误差率,将两个学习器都分别在每对数据子集上
进行训练与测试,会分别产生两组测试误差率,对每对结果求差值。若两个学习器的性能相同,则
相对应的两个误差率的差值应该为0。先计算出差值的均值μ与方差σ^2,在显著度α下,若变量根
据预先设定的显著度α,以及自由度k-1,查表可得临界值b,若Tt小于临界值则接受,否则拒绝。