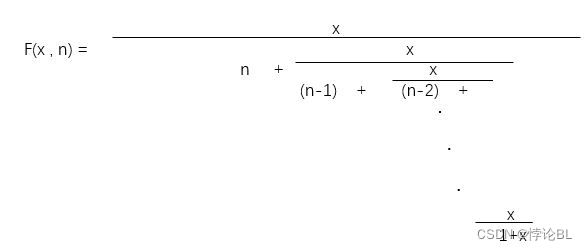数据结构与算法-C++

排序

快排

#include
using namespace std;
const int N=100010;
int q[N];
int n;
void quick_sort(int q[],int l,int r){
    if(l==r)return; //易漏
    int i=l-1,j=r+1,mid=q[l+r>>1];
    while(i<j){
        do i++;while(q[i]<mid);
        do j--;while(q[j]>mid);
        if(i<j)swap(q[i],q[j]);
    }
    quick_sort(q,l,j);
    quick_sort(q,j+1,r);
}
int main(){
    int n;cin>>n;
    for(int i=0;i<n;i++){
        scanf("%d",&q[i]);
    }
    quick_sort(q,0,n-1);
    for(int i=0;i<n;i++){
        printf("%d ",q[i]);
    }
    return 0;
}

第k个数

#include
using namespace std;
const int N=100010;
int q[N];
int n,k;
int select_sort(int q[],int l,int r){
        if(l==r)return q[l];
        int i=l-1,j=r+1,mid=q[l+r>>1];
        while(i<j){
            do i++;while(q[i]<mid);
            do j--;while(q[j]>mid);
            if(i<j)swap(q[i],q[j]);
        }
        if(k<=j)return select_sort(q,l,j);
        else return select_sort(q,j+1,r);
}
int main(){
    cin>>n>>k;
    for(int i=0;i<n;i++){
        cin>>q[i];
    }
    k--;
    cout<<select_sort(q,0,n-1);
    return 0;
}

归并排序

#include
using namespace std;
const int N=100010;
int q[N],n,temp[N];
void merge_sort(int q[],int l,int r){
    if(l==r)return;
    int mid=l+r>>1;
    int i=l,j=mid+1,k=0;
    merge_sort(q,l,mid);
    merge_sort(q,mid+1,r);
    while(i<=mid&&j<=r){
        if(q[i]<q[j]){
            temp[k++]=q[i++];
        }else{
            temp[k++]=q[j++];
        }
    }
    while(i<=mid)temp[k++]=q[i++];
    while(j<=r)temp[k++]=q[j++];
    for(int i=l,j=0;i<=r;i++,j++){
        q[i]=temp[j];
    }
}
int main(){
    cin>>n;
    for(int i=0;i<n;i++){
        cin>>q[i];
    }
    merge_sort(q,0,n-1);
    for(int i=0;i<n;i++){
        printf("%d ",q[i]);
    }
    return 0;
}

逆序对数量

#include
using namespace std;
const int N=100010;
int q[N],n,temp[N];
long res;
void merge_sort(int q[],int l,int r){
    if(l==r)return;
    int mid=l+r>>1;
    int i=l,j=mid+1,k=0;
    merge_sort(q,l,mid);
    merge_sort(q,mid+1,r);
    while(i<=mid&&j<=r){
        if(q[i]<=q[j]){ //逆序对不能相等！
            temp[k++]=q[i++];
        }else{
            temp[k++]=q[j++];
            res+=(mid-i+1); //边排序边找，如果q[i]>q[j],则左半边的q[i]之后的都大于q[j]
        }
    }
    while(i<=mid)temp[k++]=q[i++];
    while(j<=r)temp[k++]=q[j++];
    for(int i=l,j=0;i<=r;i++,j++){
        q[i]=temp[j];
    }
}
int main(){
    cin>>n;
    for(int i=0;i<n;i++){
        cin>>q[i];
    }
    merge_sort(q,0,n-1);
    cout<<res;
    return 0;
}

堆排序

堆排序：

1. 堆的结构，父节点都大于左右儿子形成大根堆，用于升序；父节点都小于左右儿子形成小根堆，用于降序。
2. 大根堆：从第一个非叶子节点开始，如果父节点大于其左右儿子节点，则不用管，否则交换父节点与左右儿子的值，递归处理下一个非叶子节点，直到堆顶得到了最大值，将其输出，并于堆底交换，缩减右边界将其移除，再递归处理得到第二大的值。

#include
#include
using namespace std;

const int N=100010;
int a[N];
int n,m; //n个数，输出前m小
int r; //右边界
void down(int u){
    int t=u; //t保持最小值点
    if(2*u<=r && a[2*u]<a[t]) t=2*u; //左儿子存在，且左儿子更小，更新父节点
    if(2*u+1<=r && a[2*u+1]<a[t]) t=2*u+1; //右儿子存在，且右儿子更小，更新右儿子
    if(u!=t){ //当前调整的点不是最小的
        swap(a[u],a[t]); //就和最小值交换
        down(t); //递归处理
    }
}

int main(){
    cin>>n>>m;
    r=n; //最开始右边界为数组长度
    for(int i=1;i<=n;i++){ //下标从1开始
        cin>>a[i];
    }
    //从第一个非叶子节点开始，从下往上递归处理
    for(int i=n/2;i>=1;i--){
        down(i);
    }
    while(m--){
        cout<<a[1]<<' '; //输出堆顶的最小值
        swap(a[1],a[r]); //将堆顶和堆底交换
        r--; //缩短边界
        down(1); //重新处理堆顶
    }
}

二分查找

区间查找

#include
using namespace std;
const int N=100010;
int q[N],n,T;
//左边界
int sl(int l,int r,int x){
    while(l<r){
        int mid=l+r>>1;  
        if(q[mid]>=x){
            r=mid;
        }else{
            l=mid+1;
        }
    }
    return l;
}
//右边界
int sr(int l,int r,int x){
    while(l<r){
        int mid=l+r+1>>1; //注意是l+r+1
        if(q[mid]<=x){
            l=mid;
        }else{
            r=mid-1;
        }
    }
    return r;
}
int main(){
    cin>>n>>T;
    for(int i=0;i<n;i++){
        scanf("%d",&q[i]);
    }
    while(T--){
        int x;
        cin>>x;
        int l=sl(0,n-1,x);
        if(q[l]!=x){
            cout<<"-1 -1"<<endl;
        }else{
            cout<<l<<" ";
            int r=sr(0,n-1,x);
            cout<<r<<endl;
        }
    }
    return 0;
}

三次方根

#include
using namespace std;
int main(){
    double x;
    cin>>x;
    double l=-1e4,r=1e4; //注意类型都是double
    while(r-l>1e-8){
        double mid=(l+r)/2;
        if(mid*mid*mid<x){
            l=mid;
        }else{
            r=mid;
        }
    }
    printf("%.6lf",l); //l/r都可以
    return 0;
}

双指针

最长连续不重复子序列

1. 遍历数组a中的每一个元素a[i], 对于每一个i，找到j使得双指针[j, i]维护的是以a[i]结尾的最长连续不重复子序列，长度为i - j + 1, 将这一长度与r的较大者更新给r。
2. 对于每一个i，如何确定j的位置：由于[j, i - 1]是前一步得到的最长连续不重复子序列，所以如果[j, i]中有重复元素，一定是a[i]，因此右移j直到a[i]不重复为止（由于[j, i - 1]已经是前一步的最优解，此时j只可能右移以剔除重复元素a[i]，不可能左移增加元素，因此，j具有“单调性”、本题可用双指针降低复杂度）。
3. 用数组s记录子序列a[j ~ i]中各元素出现次数，遍历过程中对于每一个i有四步操作：cin元素a[i] -> 将a[i]出现次数s[a[i]]加1 -> 若a[i]重复则右移j（s[a[j]]要减1） -> 确定j及更新当前长度i - j + 1给r。

#include
using namespace std;
const int N=100010;
int a[N],s[N];
int main(){
    int n,res=0;
    cin>>n;
    for(int i=0,j=0;i<n;i++){
        cin>>a[i];
        s[a[i]]++;
        while(s[a[i]]>1){
            s[a[j]]--; //j要移除
            j++; //右移动j
        }
        res=max(res,i-j+1);
    }
    cout<<res;
    return 0;
}

数组元素的目标和

i指针指向数组a的头，j指针指向数组b的尾,同时向中间走

#include
using namespace std;
const int N=100010;
int a[N],b[N];
int main(){
    int n,m,x;
    cin>>n>>m>>x;
    for(int i=0;i<n;i++)cin>>a[i];
    for(int j=0;j<m;j++)cin>>b[j];
    int i=0,j=m-1;
    while(i<n&&j>=0){
        if(a[i]+b[j]>x){
            j--;
        }else if(a[i]+b[j]<x){
            i++;
        }else{
            cout<<i<<' '<<j<<endl;
            break; //容易遗漏
        }
    }
    return 0;
}

判断子序列

i,j两个指针分别指向a,b两个数组的头部，b数组一直往后移动，a的指针当且仅当完成配对时才能往后移动，如果a的指针能指向其末尾，则能匹配完全。

#include
using namespace std;
const int N=100010;
int a[N],b[N];
int main(){
    int n,m;
    cin>>n>>m;
    for(int i=0;i<n;i++)cin>>a[i];
    for(int j=0;j<m;j++)cin>>b[j];
    int i=0,j=0;
    while(i<n&&j<m){
        if(a[i]==b[j])i++;
        j++;
    }
    if(i==n)puts("Yes");
    else puts("No");
    return 0;
}

数据结构

表达式求值

使用双栈，分别存储数字和运算符
首先指定运算符的优先级，栈顶优先级大于将要入栈的，则先取出栈顶元素进行计算，否则运算符入栈

#include
using namespace std;
stack<int>num;
stack<char>op;

//优先级：栈顶优先级高，则先计算栈顶，否则运算符入栈
unordered_map<char,int> umap={{'+',1},{'-',1},{'*',2},{'/',2}};

//从栈中取出两个数进行运算
void eval(){
    int a=num.top();
    num.pop();
    int b=num.top();
    num.pop();
    char ops=op.top();
    op.pop();
    if(ops=='+')num.push(a+b);
    else if(ops=='-')num.push(b-a);
    else if(ops=='*')num.push(a*b);
    else if(ops=='/')num.push(b/a);
}
int main(){
    string s;
    cin>>s;
    for(int i=0;i<s.size();i++){
        if(isdigit(s[i])){ //将字符转化为数字
            int x=0,j=i;
            while(j<s.size()&&isdigit(s[j])){
                x=10*x+(s[j]-'0');
                j++;
            }
            num.push(x);
            i=j-1;
        }else if(s[i]=='('){ //左括号直接入栈
            op.push(s[i]);
        }else if(s[i]==')'){ //取出（）内的式子并进行计算
            while(op.top()!='('){
                eval();
            }
            op.pop(); //'('出栈
            
        }else{  //运算符比较优先级进行计算
            while(op.size()&&umap[op.top()]>=umap[s[i]]){ //栈不为空且栈顶优先级更大
                eval();
            }
            op.push(s[i]); //运算符入栈
        }
    }
    while(op.size()){ //计算完
        eval();
    }
    int res=num.top();
    cout<<res<<endl;
    return 0;
}

单调栈

#include
using namespace std;
const int N=100010;
int stk[N],tt;
int main(){
    int n;
    cin>>n;
    for(int i=0;i<n;i++){
       int x;
       cin>>x;
       while(tt&&stk[tt]>=x)tt--; //如果栈顶大于x就往前找
       if(tt)cout<<stk[tt]<<' '; //能找到就输出
       else cout<<"-1"<<' ';
       stk[++tt]=x; //插入
    }
    return 0;
}

滑动窗口最值

给定一个包含n个数的数组，指定滑动窗口的宽度为k,求出每一个滑动窗口中的最小值和最大值.

#include
using namespace std;
const int N=1000010;
int q[N],a[N];
int main(){
    int n,k;
    cin>>n>>k;
    for(int i=0;i<n;i++){
        cin>>a[i];
    }
    int hh=0,tt=-1;
    //窗口最小值
    for(int i=0;i<n;i++){
        if(hh<=tt&&i-k+1>q[hh])hh++; //窗口头部往左移动
        while(hh<=tt&&a[q[tt]]>=a[i])tt--; //比a[i]大,则应该排在a[i]后面,保证单调自增
        q[++tt]=i; //q[++tt]是a[i]插入的下标
        if(i-k+1>=0)cout<<a[q[hh]]<<' '; //队列单增，遍历完一个窗口，队头就是窗口最小值
    }
    cout<<endl;
    //重置队头和队尾
    hh=0,tt=-1;
    
    //窗口最大值
    for(int i=0;i<n;i++){
        if(hh<=tt&&i-k+1>q[hh])hh++; //窗口头部往左移动
        while(hh<=tt&&a[q[tt]]<=a[i])tt--; //比a[i]大,则应该排在a[i]后面,保证单调自增
        q[++tt]=i; //q[++tt]是a[i]插入的下标
        if(i-k+1>=0)cout<<a[q[hh]]<<' '; //队列单减,遍历完一个窗口，队头就是窗口最大值
    }
    return 0;
}

并查集

举例说明：

{0,1,2}, {3,4,5} => [0,0,0,3,3,3]：第一个数组是0, 1, 2, 3, 4, 5，第二个数组是0, 0, 0, 3, 3, 3。第一个数组保存了所有元素，第二个数组保存了元素所属集合。

第二个数组中，第一个元素是0，含义是：第一个数组的第一个元素属于 0 号集合。
第二个数组中，第二个元素是0，含义是：第一个数组的第二个元素属于 0 号集合。
第二个数组中，第三个元素是0，含义是：第一个数组的第三个元素属于 0 号集合。
第二个数组中，第四个元素是3，含义是：第一个数组的第四个元素属于 3 号集合。
第二个数组中，第五个元素是3，含义是：第一个数组的第五个元素属于 3 号集合。
第二个数组中，第六个元素是3，含义是：第一个数组的第六个元素属于 3 号集合。

可以为每个元素选出一个代表它的元素，数组二中存放代表元素

1. 用一个数组保存对应位置元素所属集合的代表元素。
2. AB两个集合合并：将B集合代表元素的代表元素设置为A集合的代表元素。
3. 查找C元素属于哪个集合：找C元素的代表元素，如果不是他自己，就重复查找代表元素的代表元素，知道查找到一个元素的代表元素是它自己，C就属于整个代表元素所代表的集合

#include
using namespace std;
const int N=100010;
int p[N]; //存放代表元素

//找到x对应的集合的代表元素
int find(int x){ 
    if(p[x]!=x){ //如果代表元素不是本身，就递归找到所在集合的代表元素
        p[x]=find(p[x]); 
    }
    return p[x];
}

void merge(int a,int b){
    int pa=find(a); //查找到a对应的代表元素
    int pb=find(b); //查找到b对应的代表元素
    if(pa!=pb){ //如果代表元素不同，则不在同一个集合
        p[pa]=pb; //将a的代表元素设置为b的代表元素
    }
}

void query(int a,int b){
    int pa=find(a);
    int pb=find(b);
    if(pa==pb){
        puts("Yes");
    }else{
        puts("No");
    }
}
int main(){
    int n,m;
    cin>>n>>m;
    for(int i=0;i<n;i++){
        p[i]=i; //初始化集合，每个点属于单独的集合
    }
    while(m--){
        char op[2];
        int a,b;
        cin>>op>>a>>b;
        if(*op=='M'){
            merge(a,b);
        }else{   
            query(a,b);   
        }
    }
    return 0;
}

动态规划

子序列问题

最大连续子序列乘积

输入n个元素组成的序列S，你需要找出一个乘积最大的连续子序列，如果这个最大的乘积不是正数，则输出-1

#include
#include
#include
#include
using namespace std;

const int N=20;
int a[N];
double max(double a,double b){return a>b?a:b;}
double min(double a,double b){return a>b?b:a;}
double dp_max[20],dp_min[20],res; //以a[i]结尾的最大和最小连续乘积
int main(){
    int n;
    while(cin>>n){
        for(int i=0;i<n;i++){
            cin>>a[i];
        }
        dp_max[0]=a[0],dp_min[0]=a[0];
        for(int i=1;i<n;i++){
            dp_max[i]=max(max(dp_max[i-1]*a[i],dp_min[i-1]*a[i]),a[i]);
            dp_min[i]=min(min(dp_max[i-1]*a[i],dp_min[i-1]*a[i]),a[i]);
        }
        res=dp_max[0];
        for(int i=1;i<n;i++){
            res=max(res,dp_max[i]);
        }
        if(res>0){
            printf("%.0lf\n",res);
        }else{
            printf("-1\n");
        }
    }
    return 0;
}

最大连续子序列和及下标

#include
#include
using namespace std;
const int N=100000;
int n;
int num[N];
int main(){
    while(cin>>n){
        int dp[N]; //以num[i]结尾的子序列和
        for(int i=1;i<=n;i++){
            cin>>num[i];
            dp[i]=num[i];
        }
        int res=-1,l=0,r=0,temp=0; 
        for(int i=1;i<=n;i++){
            dp[i]=max(num[i],dp[i-1]+num[i]);
            if(dp[i-1]<0)temp=i-1; //前i-1的和为负数，则都不取，左边界从下一个位置开始
            if(dp[i]>res){ //更新左右边界
                res=dp[i];
                l=temp;
                r=i-1;
            }
        }
        if(res<0){
           printf("0 0 0\n");
        }else{
            cout<<res<<' '<<l<<' '<<r<<endl;
        }
    }
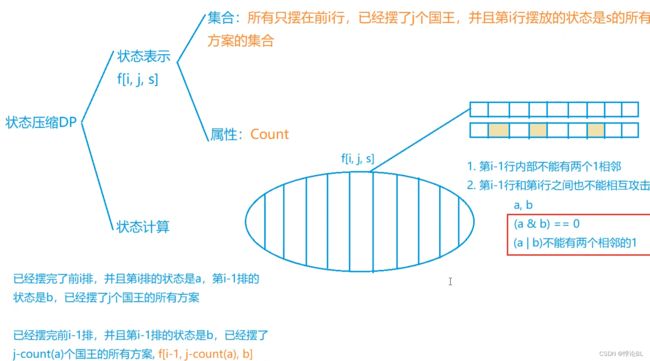
    return 0;
}

状态压缩dp

小国王

#include
using namespace std;

const int N=12,M=1<<10,K=110;
vector<int>state; //所有状态
vector<int>head[M]; //所有能转移的状态
int cnt[M]; //计算每一行1的个数
int n,m;
typedef long long LL;
LL f[N][K][M]; //摆了N行,一共摆了K个，第i行状态是M的方案集合

//同一行不能有相邻的1
bool check(int state){
    if(!(state&state>>1)){
        return true;
    }
    return false;
}
//计算state状态下1的个数，即可以放置的国王个数
int count(int state){
    int res=0;
    for(int i=0;i<n;i++){
        res+=state>>i&1; //二进制中1的个数(对应放置国王的个数)
    }
    return res;
}
int main(){
    cin>>n>>m;
    //筛选出所有合法的状态
    for(int i=0;i<1<<n;i++){
        if(check(i)){
            state.push_back(i); //记录该状态
            cnt[i]=count(i); //记录该状态下1的个数（能放置国王的个数）
        }
    }
    //枚举出所有可以转移的状态
    for(int i=0;i<state.size();i++){
        for(int j=0;j<state.size();j++){
            int a=state[i],b=state[j];
            if(!(a&b) && check(a|b)){ //相邻两行要错开且不能含有相邻的1
                head[a].push_back(b); //a,b状态可以转移
            }
        }
    }
    //初始化
    f[0][0][0]=1;
    for(int i=1;i<=n+1;i++){
        for(int j=0;j<=m;j++){
            for(auto a:state){
                for(auto b:head[a]){
                    if(j>=cnt[a]){ //剩余国王个数
                       f[i][j][a]+=f[i-1][j-cnt[a]][b]; 
                    }
                }
            }
        }
    }
    //摆了n+1行，m个国王，最后一行状态为0的方案数
    cout<<f[n+1][m][0]<<endl;
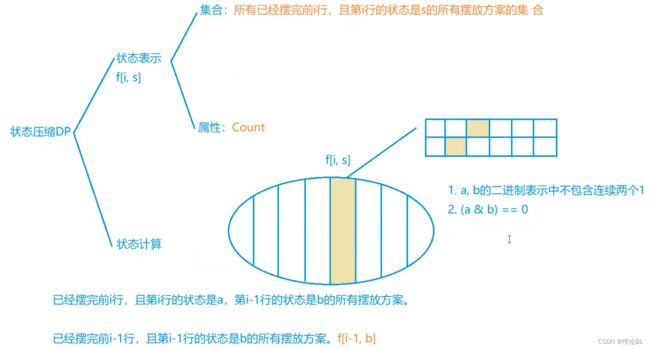
    return 0;
}

玉米田

#include
#include
#include
using namespace std;

const int N=14,M=1<<12,mod=1e8;
int n,m;
int f[N][M];
int g[N]; //存储田地的二进制状态
vector<int>state;
vector<int>head[M];

//判断同一行state状态下是否有相邻的1
bool check(int state){
    for(int i=0;i<m;i++){
        if((state >> i & 1)&&(state>>(i+1)& 1)){
            return false;
        }
    }
    return true;
}

int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        for(int j=0;j<m;j++){
            int t;
            cin>>t;
            g[i]+=!t<<j; //记录田地的二进制状态
        }
    }
    //合法状态
    for(int i=0;i<1<<m;i++){
        if(check(i)){
            state.push_back(i);
        }
    }
    //合法状态转移
    for(int i=0;i<state.size();i++){
        for(int j=0;j<state.size();j++){
            int a=state[i],b=state[j];
                if((a & b)==0){ //相邻两行不能包含相邻的1
                    head[i].push_back(j);
            }
        }
    }
    //状态计算
    f[0][0]=1; //初始化
    for(int i=1;i<=n+1;i++){
        for(int a=0;a<state.size();a++){
            for(auto b:head[a]){
                if(g[i]&state[a])continue; //土地不育，无法种植
                f[i][a]=(f[i][a]+f[i-1][b])%mod;
            }
        }
    }
    cout<<f[n+1][0]<<endl;
    return 0;
}

区间dp

环形石子合并

可以将一个环用首尾相连的两条链取代，在两条链上做一遍区间dp

#include
using namespace std;

const int N=410,INF=0x3f3f3f3f;
int n; //n堆石子
int w[N]; //石子代价
int s[N]; //前缀和
int f[N][N],g[N][N]; //f是最大值,g是最小值
int main(){
    //初始化数组
    memset(f,-0x3f,sizeof f);
    memset(g,0x3f,sizeof g);
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>w[i];
        w[i+n]=w[i]; //形成首尾相连的两条链
    }
    //前缀和
    for(int i=1;i<=2*n;i++){
        s[i]=s[i-1]+w[i];
    }
    for(int len=1;len<=n;len++){ //枚举区间长度
        for(int l=1;l+len-1<=n*2;l++){ //枚举左端点长度
            int r=l+len-1;
            if(len==1){
                f[l][r]=g[l][r]=0; //长度为一合并代价为0
            }else{
                for(int k=l;k<r;k++){ //枚举分割点
                    //状态转移,合并l~r的代价--->合并l~k和k+1~r,再加上l~r石子本身的代价
                    f[l][r]=max(f[l][r],f[l][k]+f[k+1][r]+s[r]-s[l-1]);
                    g[l][r]=min(g[l][r],g[l][k]+g[k+1][r]+s[r]-s[l-1]);
                }
            }
        }
    }
    int max_value=-INF;
    int min_value=INF;
    for(int i=1;i<=n;i++){
        max_value=max(max_value,f[i][i+n-1]);
        min_value=min(min_value,g[i][i+n-1]);
    }
    cout<<min_value<<endl<<max_value<<endl;
}

搜索与图论

DFS

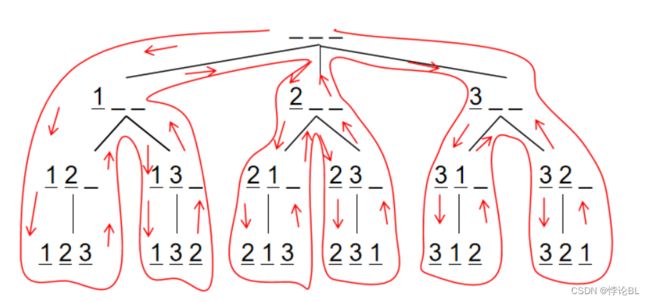
排列数字

for循环横向遍历，递归回溯横向遍历

#include
using namespace std;
const int N=100010;
int n;
int path[N];
bool used[N];
void dfs(int u){
    if(u>n){
        for(int i=1;i<=n;i++){
            cout<<path[i]<<' ';
        }
        cout<<endl;
    }
    for(int i=1;i<=n;i++){
        if(!used[i]){
            used[i]=true;
            path[u]=i; //将该数加入序列
            dfs(u+1); //进入到下一次递归时
            used[i]=false; //将该数的状态改变为未使用
        }
    }
}
int main(){
    cin>>n;
    dfs(1);
}

Flood Fill算法

池塘计数

#include
#include
using namespace std;
const int N=1010;
int dx[8]={0,0,-1,1,-1,1,-1,1}; //记录8个方向的坐标变化
int dy[8]={1,-1,0,0,-1,-1,1,1}; //上左下右左上左下右上右下
char mp[N][N]; //存储地图
int n,m; //地图的长和宽
int ans; //池塘个数

void dfs(int x,int y){
    mp[x][y]='.'; //更新当前节点类型?
    for(int i=0;i<8;i++){
        if(mp[x+dx[i]][y+dy[i]]=='W'){
            dfs(x+dx[i],y+dy[i]); //dfs下一个点
        }
    }
}
int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            cin>>mp[i][j];
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
             if(mp[i][j]=='W'){ //如果有水就dfs
                 dfs(i,j);
                 ans++;
             }
        }
    }
    cout<<ans<<endl;
}

城堡问题

输入处理

#include
#include
#define x first
#define y second
using namespace std;
typedef pair<int,int>PII;

const int N=55,M=N*N;
PII q[M]; //模拟队列的数组
bool st[N][N]; //标记是否遍历过
int map[N][N]; //地图
int n,m; //地图的长和宽
int ans,area; //连通块个数和面积
int dx[4]={0,-1,0,1},dy[4]={-1,0,1,0}; //西北东南四个方位的坐标变化

int bfs(int sx,int sy){
    int hh=0,tt=0;
    int area=0;
    
    //初始化队头
    q[0]={sx,sy}; 
    st[sx][sy]=true;
    
    while(hh<=tt){
        PII t=q[hh++]; //取出队头
        area++;
        for(int i=0;i<4;i++){ 
            int a=t.x+dx[i],b=t.y+dy[i]; //可以拓展的点
            if(a<0||a>=n||b<0||b>=m)continue; //越界判断
            if(st[a][b])continue; //去重
            if(map[t.x][t.y]>>i&1)continue; //第i位是1，表示有障碍物，要跳过
            q[++tt]={a,b};
            st[a][b]=true;
        }
    }
    return area;
}

int main(){
    cin>>n>>m;
    for(int i=0;i<n;i++){
        for(int j=0;j<m;j++){
            cin>>map[i][j];
        }
    }
    for(int i=0;i<n;i++){
        for(int j=0;j<m;j++){
            if(!st[i][j]){
                ans++;
                area=max(area,bfs(i,j));
               }
            }
        }
        cout<<ans<<endl;
        cout<<area<<endl;
        return 0; 
}

山峰和山谷

找到高度一致的连通块，若该连通块周围
没有存在比它高的则该连通块叫山峰
没有存在比它矮的则该连通块叫山谷

#include
#include
#include
#define x first
#define y second
using namespace std;
typedef pair<int,int>PII;
const int N=1010;
int n;
int h[N][N];
bool st[N][N];
bool has_higher,has_lower; //分别标记山峰和山谷
void bfs(int sx,int sy){
    queue<PII>q;
    q.push({sx,sy});
    while(!q.empty()){
        PII t=q.front();
        q.pop();
        for(int i=t.x-1;i<=t.x+1;i++){
            for(int j=t.y-1;j<=t.y+1;j++){
                if(i<1||i>n||j<1||j>n)continue; //越界处理
                if(h[i][j]!=h[t.x][t.y]){ //旁边的高度不一样
                    if(h[i][j]>h[t.x][t.y])has_higher=true; //旁边的更高
                    else has_lower=true; //旁边的更低
                }else if(!st[i][j]){ //没有被搜索过，就加入队列
                    q.push({i,j});
                    st[i][j]=true;
                }
            }
        }
    }
}
int main(){
    cin>>n;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            cin>>h[i][j];
        }
    }
    int peak=0,vally=0;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            if(!st[i][j]){
                has_higher=false,has_lower=false;
                bfs(i,j);
                if(!has_higher)peak++; //山峰没有被标记过，则山峰+1
                if(!has_lower)vally++; //山谷没有被标记过，则山谷+1
            }
        }
    }
    cout<<peak<<' '<<vally<<endl;
    return 0;
}

最短路模型

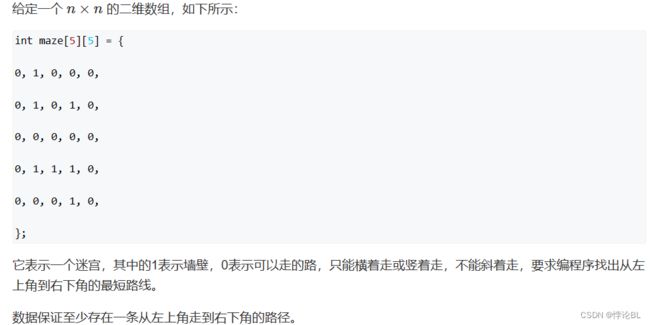
迷宫路径

从(0, 0)向(n - 1, n - 1)搜索可以等价为从(n - 1, n - 1)向(0, 0)搜索. 我们不妨从(n - 1,
n - 1)向(0, 0)搜索. 那这样做有何优势？ 在搜索的过程中，我们很容易记下当前位置的前驱,下标n - 1必然是下标n - 1
到0之间某个位置的前驱,n - 2 也必然 是n - 2
到0之间某个位置的下标的前驱,依次类推···打印的时候,我们逆序打印,打印完(0,0)后,再打印他的前驱位置,
以此类推···那么当我们逆序打印(0,0) 到 (n - 1, n - 1)之间记录的下标时,便是由(0,0)到(n - 1, n -
1)的路径.

#include
#include
#include
#include

#define x first
#define y second

using namespace std;
typedef pair<int,int>PII;

const int N=1010;
int n;
int g[N][N];
bool st[N][N];
PII pre[N][N];
int dx[4]={-1,0,1,0},dy[4]={0,-1,0,1};
queue<PII>q;

void bfs(){
    q.push({n-1,n-1});
    st[n-1][n-1]=true;
    while(q.size()){
        PII t=q.front();
        q.pop();
        for(int i=0;i<4;i++){
            int x=t.x+dx[i],y=t.y+dy[i];
            if(x>=0&&x<n&&y>=0&&y<n&&g[x][y]==0&&!st[x][y]){
                st[x][y]=true;
                pre[x][y]=t; //记录前驱
                q.push({x,y});
            }
        }
    }
    int x=0,y=0;
    while(x!=n-1||y!=n-1){
        cout<<x<<' '<<y<<endl;
        PII t=pre[x][y]; //前驱坐标
        x=t.x,y=t.y; //更新当前的前驱
    }
    cout<<n-1<<' '<<n-1<<endl;
}

int main(){
    cin>>n;
    for(int i=0;i<n;i++){
        for(int j=0;j<n;j++){
            cin>>g[i][j];
        }
    }
    bfs();
    return 0;
}

最短距离–走日字

从K点出发，按照日字形走，*为障碍物，求到达H点的最短距离

#include
#include
#include
#include
#define x first 
#define y second
using namespace std;
const int N=155;
typedef pair<int,int>PII;
queue<PII>q;
char g[N][N]; //存储地图
int n,m; //行列
int dist[N][N]; //存储距离
int dx[8]={1,2,2,1,-1,-2,-2,-1}; //八个方位的点坐标
int dy[8]={2,1,-1,-2,-2,-1,1,2};

int bfs(){
    memset(dist,-1,sizeof dist); //初始化距离
    int sx=0,sy=0; //起点K的位置
    for(int i=0;i<n;i++){
        for(int j=0;j<m;j++){
            if(g[i][j]=='K'){
                sx=i,sy=j;
                break;
            }
        }
    }
    q.push({sx,sy});
    dist[sx][sy]=0;
    while(q.size()){
        PII t=q.front();
        q.pop();
        for(int i=0;i<8;i++){
            int a=dx[i]+t.x,b=dy[i]+t.y;
            if(a<0||a>=n||b<0||b>=m)continue;
            if(g[a][b]=='*')continue; //跳过障碍物
            if(dist[a][b]!=-1)continue; //已经走过的点
            if(g[a][b]=='H')return dist[t.x][t.y]+1; //到达终点
            q.push({a,b});
            dist[a][b]=dist[t.x][t.y]+1; //更新距离
        }
    }
    
}
int main(){
    cin>>m>>n;
    for(int i=0;i<n;i++){
        for(int j=0;j<m;j++){
            cin>>g[i][j];
        }
    }
    cout<<bfs();
    return 0;
}

抓住那头牛

#include
#include
#include
#include
using namespace std;
const int N=2e5+10;
queue<int>q;
int dist[N]; //dist[k]表示到终点的最短距离
int n,k; //起点和终点
int bfs(){
    memset(dist,-1,sizeof dist); 
    q.push(n);
    dist[n]=0; //初始化起点距离
    while(q.size()){
        int t=q.front();
        q.pop();
        if(t==k)return dist[k]; //走到终点返回
        //向右走1步
        if(t+1<N&&dist[t+1]==-1){
            dist[t+1]=dist[t]+1; //更新距离
            q.push(t+1);
        }
        //向左走1步
        if(t-1>=0&&dist[t-1]==-1){
            dist[t-1]=dist[t]+1;
            q.push(t-1);
        }
        //走到2*N
        if(2*t<N&&dist[2*t]==-1){
            dist[2*t]=dist[t]+1;
            q.push(2*t);
        }
    }
    return -1;
}
int main(){
    cin>>n>>k;
    cout<<bfs()<<endl;
    return 0;
}

最小步数模型

魔板

这是一张有 8 个大小相同的格子的魔板：

1 2 3 4
8 7 6 5

对于上图的魔板状态，我们用序列 (1,2,3,4,5,6,7,8) 来表示，这是基本状态。

这里提供三种基本操作，分别用大写字母 A，B，C 来表示（可以通过这些操作改变魔板的状态）：

A：交换上下两行；
B：将最右边的一列插入到最左边；
C：魔板中央对的4个数作顺时针旋转。

下面是对基本状态进行操作的示范：

A：

8 7 6 5
1 2 3 4
B：

4 1 2 3
5 8 7 6
C：

1 7 2 4
8 6 3 5
对于每种可能的状态，这三种基本操作都可以使用。

你要编程计算用最少的基本操作完成基本状态到特殊状态的转换，输出基本操作序列。

输入仅一行，包括 8 个整数，用空格分开，表示目标状态。

输出格式
输出文件的第一行包括一个整数，表示最短操作序列的长度。

如果操作序列的长度大于0，则在第二行输出字典序最小的操作序列。

#include
#include
#include
#include
#include
using namespace std;

unordered_map<string,int>dist; //<得到目标字符串(string),需要的操作数(int)>
unordered_map<string,pair<char,string>>pre; //<当前字符串(string),<上一次的操作(char),上一次的字符串(string)> 
queue<string>q;
string st,ed,res;

string move0(string t){ 
    /*交换上下两行
        1 2 3 4 -> 8 7 6 5
        8 7 6 5 -> 1 2 3 4
    */
    for(int i=0;i<4;i++){
        swap(t[i],t[7-i]); 
    }
    return t;
}
string move1(string t){ 
    /*所有列往右移一列
       1 2 3 4 -> 4 1 2 3 
       8 7 6 5 -> 5 8 7 6
    */
    for(int i=0;i<3;i++)swap(t[3],t[i]);
    for(int i=4;i<7;i++)swap(t[i],t[i+1]);
    return t;
}
string move2(string t){ 
    /*顺时针旋转中心
        1 2 3 4 -> 1 7 2 4
        8 7 6 5 -> 8 6 3 5
    */
    swap(t[1],t[2]);
    swap(t[5],t[6]);
    swap(t[1],t[5]);
    return t;

}
void bfs(string st,string ed){
    q.push(st);
    while(q.size()){
        string t=q.front();
        q.pop();
        if(t==ed)return;
        string m[3]; //操作
        m[0]=move0(t);
        m[1]=move1(t);
        m[2]=move2(t);
        for(int i=0;i<3;i++){ //按照0 1 2顺序操作保证字典序最小
            if(!dist.count(m[i])){ //当前状态没有被计算过
                q.push(m[i]);
                dist[m[i]]=dist[t]+1; //更新距离
                pre[m[i]]={'A'+i,t}; //记录前驱的操作和字符串
            }
        }
    }
}
int main(){
    for(int i=0;i<8;i++){
        int x;cin>>x;
        ed+=(char)(x+'0');
        st+=(char)(i+'1'); //12345678
    }
    bfs(st,ed);
    cout<<dist[ed]<<endl;
    if(dist[ed]){
        while(ed!=st){
            res+=pre[ed].first;
            ed=pre[ed].second;
        }
        reverse(res.begin(),res.end());
        cout<<res<<endl;
    }
    return 0;
}

多源BFS

矩阵距离

给定一个n行m列的01矩阵，要求输出所有0到1的最短距离

将所有1作为起点加入队列中，第一次宽搜到0的距离就是最短距离.

#include
#include
#include
using namespace std;
const int N=1010;
#define x first
#define y second
typedef pair<int,int>PII;
queue<PII>q;
char g[N][N];
int dist[N][N];
int n,m;
int dx[4]={-1,1,0,0},dy[4]={0,0,-1,1};
void bfs(){
    for(int i=0;i<n;i++){
        for(int j=0;j<m;j++){
            if(g[i][j]=='1'){ //将所有的1作为起点加入队列，并初始化距离为1
                q.push({i,j});
                dist[i][j]=0;
            }
        }
    }
    while(q.size()){
        PII t=q.front();
        q.pop();
        for(int i=0;i<4;i++){
            int a=t.x+dx[i],b=t.y+dy[i];
            if(a<0||a>=n||b<0||b>=m)continue;
            if(dist[a][b]!=-1)continue; //距离已经被更新过
            dist[a][b]=dist[t.x][t.y]+1; //更新距离
            q.push({a,b});
        }
    }
}
int main(){
    memset(dist,-1,sizeof dist);
    scanf("%d %d",&n,&m);
    for(int i=0;i<n;i++){
        scanf("%s",g[i]);
    }
    bfs();
    for(int i=0;i<n;i++){
        for(int j=0;j<m;j++){
            printf("%d ",dist[i][j]);
        }
        cout<<endl;
    }
    return 0;
}

双端队列广搜

电路板

电路板的整体结构是一个 R 行 C 列的网格（R,C≤500），如下图所示。

每个格点都是电线的接点，每个格子都包含一个电子元件。

电子元件的主要部分是一个可旋转的、连接一条对角线上的两个接点的短电缆。

在旋转之后，它就可以连接另一条对角线的两个接点。

电路板左上角的接点接入直流电源，右下角的接点接入飞行车的发动装置。

达达发现因为某些元件的方向不小心发生了改变，电路板可能处于断路的状态。

她准备通过计算，旋转最少数量的元件，使电源与发动装置通过若干条短缆相连。

利用双端队列,如果权重为1就加入队尾，如果权重为0加入队头

#include
#include
#include
#include
using namespace std;
const int N=510;
typedef pair<int,int> PII;

char g[N][N];
int dist[N][N];
int w;
int n,m;

bool check(int x,int y){
    if(x>=0 && x<=n && y>=0 && y<=m){
        return true;
    } 
    return false;
}
int bfs(){
    memset(dist,0x3f,sizeof dist);
    deque<PII>dq;
    dq.push_front({0,0});
    dist[0][0]=0;
    int move[4][2]={
        {-1,-1},
        {-1,1},
        {1,1},
        {1,-1},
    };
    int movei[4][2]={
        {-1,-1},
        {-1,0},
        {0,0},
        {0,-1},
    };
    char cp[]="\\/\\/";
    while(dq.size()){
        auto t=dq.front();
        dq.pop_front();
        int x=t.first,y=t.second;
        for(int i = 0 ;i < 4; i ++){
            int a= x + move[i][0],b= y + move[i][1];
            if(check(a,b)){
                int j= x + movei[i][0],k= y + movei[i][1];
                if(g[j][k]!=cp[i])w=1;
                else w=0;
                if(dist[a][b] > dist[x][y] + w){
                    dist[a][b] = dist[x][y] + w;
                    if(w)dq.push_back({a,b});
                    else dq.push_front({a,b});
                }
            }
        }
    }
    if(dist[n][m]==0x3f3f3f3f)return -1;
    else return dist[n][m];
}

void solve(){
    cin>>n>>m;
    for(int i=0;i<n;i++)cin>>g[i];
    int res=bfs();
    if(res==-1){
        cout<<"NO SOLUTION"<<endl;
    }else{
        cout<<res<<endl; 
    } 
}
int main(){
    int T;
    cin>>T;
    while(T--){
        solve();
    }
    return 0;
}

数学

质素判断

#include
using namespace std;
bool is_prime(int x){
    if(x<2)return false;
    for(int i=2;i<=x/i;i++){
        if(x%i==0){
            return false;
        }
    }
    return true;
}
int main(){
    int n;
    cin>>n;
    while(n--){
        int x;
        cin>>x;
        if(is_prime(x)){
            cout<<"Yes"<<endl;
        }else{
            cout<<"No"<<endl;
        }
    }
    return 0;
}

质素筛

#include
using namespace std;
const int N=1000010;
int st[N]; //标记是否筛过
int prime[N]; //质素数组
int cnt;
void get_prime(int n){
    for(int i=2;i<=n;i++){
        if(!st[i])prime[cnt++]=i; //i是数组，则加入质素数组
        for(int j=i;j<=n;j+=i){ //i的倍数不是质素，应该筛掉
            st[j]=true; 
        }
    }
}
int main(){
    int n;
    cin>>n;
    get_prime(n);
    //输出
    // for(int i=0;i
    //     cout<
    // }
    cout<<cnt<<endl;
    return 0;
}

四舍五入

1. 取整:(int)(浮点数+0.5)

#include
using namespace std;
int main(){
	int n,m;
	cin>>n>>m;
	double c=n*1.0/m; //注意是浮点数除法
	cout<<(int)(c+0.5)<<endl;
	return 0;
}

2. 保留3位小数 (int)(x*1000+0.5)/1000.0

#include
using namespace std;
int main(){
	double n=3.1415;
	cout<<(int)(n*1000+0.5)/1000.0<<endl; 
	return 0;
}

3. 使用库函数

#include
#include
using namespace std;
int main(){
	double n=3.1415;
	cout<<round(n*1000)/1000; //保留三位小数
	return 0;
}

分解质因数

#include
using namespace std;
int main(){
	int n;cin>>n;
	for(int i=2;n>1;i++){
		while(n%i==0){
			printf("%d",i);
			n/=i;
			if(n==1)cout<<endl; //分解完毕
			else cout<<' ';
		}
	}
	return 0;
}

回文素数

输出n~m之间的回文素数

#include
#include
#include
using namespace std;

int primes[10000000];
bool st[10000000];
int cnt;

bool is_hui(int n){
    int m=n;
    int sum=0;
    for(int i=n;i>0;i/=10){
        sum=10*sum+i%10;
    }
    if(m==sum){
        return true;
    }else{
        return false;
    }
}

void get_primes(int n){
    for(int i=2;i<=n;i++){
        if(!st[i])primes[cnt++]=i;
        for(int j=i;j<=n;j+=i){
            st[j]=true;
        }
    }
}
int main(){
    int n,m;
    scanf("%d %d",&n,&m);
    get_primes(m);
    for(int i=0;i<cnt;i++){
       if(is_hui(primes[i]) && primes[i]>=n){
           cout<<primes[i]<<endl;
       } 
    }
    return 0;
}

高精度加法

#include
#include
#include
using namespace std;
int a[110],b[110],c[110];
int main(){
	string str1,str2;
	cin>>str1>>str2;
	for(int i=0;i<str1.size();i++){
		a[str1.size()-1-i]=str1[i]-'0';
	}
	for(int j=0;j<str2.size();j++){
		b[str2.size()-1-j]=str2[j]-'0';
	}
	int len=max(str1.size(),str2.size());
	for(int i=0;i<len;i++){
		c[i]=c[i]+a[i]+b[i];
		c[i+1]=c[i]/10;
		c[i]%=10;
	}
	len+=1;
	if(c[len-1]==0 && len>1){ //检验最高位是否为零
		len-=1;
	}
	for(int i=0;i<len;i++){
		cout<<c[len-1-i]; //逆序输出
	}
	return 0;
}

高精度减法

#include
using namespace std;
int a[110],b[110],c[110];
int flag=0;
int main(){
	string str1,str2;
	cin>>str1>>str2;
	if(atoi(str1.c_str())<atoi(str2.c_str()) && str1.size()==str2.size() || str1.size()<str2.size()){
		swap(str1,str2);
		flag=1;		
	}
	for(int i=0;i<str1.size();i++){
		a[str1.size()-1-i]=str1[i]-'0';
	}
	for(int i=0;i<str2.size();i++){
		b[str2.size()-i-1]=str2[i]-'0';
	}
	int len=max(str1.size(),str2.size());
	for(int i=0;i<len;i++){
		if(a[i]<b[i]){
			a[i+1]-=1;
			a[i]+=10;
		}c[i]=a[i]-b[i];
	}
	while(c[len-1]==0 && len>1){ //取出前导零 
		len-=1;
	}
	if(flag){
		cout<<'-';
	}
	for(int i=0;i<len;i++){
		cout<<c[len-1-i];
	}
	return 0;
}

任意进制转10进制

int to_10(string s,int b){ //将b进制的s转化为10进制 
	int num=0;
	for(int i=0;i<s.size();i++){
		num=num*b+s[i]-'0';
	}
	return num;
}

数组

数组平移

将a数组中第一个元素移到数组末尾，其余数据依次往前平移一个位置。

#include
using namespace std;
int main(){
    int n;cin>>n;
    int q[1000];
    for(int i=0;i<n;i++){
        cin>>q[i];
    }
    int temp=q[0]; //保存头部元素
    for(int i=0;i<n;i++){ //数组全部从后往前赋值
        q[i]=q[i+1];
    }
    q[n-1]=temp; //尾部元素单独再赋值一遍
    for(int i=0;i<n;i++){
        cout<<q[i]<<' ';
    }
    return 0;
}

从大到小 排序

将10个数从大到小排序

#include
#include
using namespace std;
bool cmp(int a,int b){
    return a>b; //从大到小
}
int main(){
    int q[10];
    for(int i=0;i<10;i++){
        cin>>q[i];
    }
    sort(q,q+10,cmp);
    for(int i=0;i<10;i++){
        cout<<q[i]<<' ';
    }
    return 0;
}

杨辉三角

打印杨辉三角前10行

#include
using namespace std;
int q[11][11];
int main(){
    for(int i=1;i<=10;i++){
        q[i][1]=1,q[i][i]=1;
       for(int j=2;j<i;j++){ //第二列~倒数第二列
            q[i][j]=q[i-1][j]+q[i-1][j-1];
        }
    }
    for(int i=1;i<=10;i++){
        for(int k=1;k<=10-i;k++){
            cout<<"   ";
        }
        for(int j=1;j<=i;j++){
            printf("%6d",q[i][j]); //格式输出
        }
        cout<<endl;
    }
    return 0;
     
}

回文数的判断

输入一串字符，字符个数不超过100，且以“.”结束。判断它们是否构成回文。“Yes”/“No”

#include
#include
using namespace std;
char s[1000];
char s2[1000];
bool is_huiwen(char s[]){
    for(int i=0,j=strlen(s)-1;i<j;i++,j--){
        if(s[i]!=s[j]){
            return false;
        }
    }
    return true;
}
int main(){
    cin>>s;
    int j=0;
    for(int i=0;i<strlen(s)-1;i++){
        s2[j++]=s[i];
    }
    if(is_huiwen(s2)){
        cout<<"Yes"<<endl;
    }else{
        cout<<"No"<<endl;
    }
    return 0;
}

约瑟夫环

N个人围成一圈，从第一个人开始报数，数到M的人出圈；再由下一个人开始报数，数到M的人出圈；……输出依次出圈的人的编号。N，M由键盘输入。

使用指针p循环遍历,每次当遍历到m时，标记为出局,并输出编号

#include
using namespace std;
bool isOut[100];
int n,m,p; //p指向当前遍历到的位置
int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){ //一共输出n次
        for(int j=0;j<m-1;j++){ //循环m-1次，p指向m的前一个位置
            while(isOut[p]==true){ 
                p=(p+1)%n; //已经出局就跳过
            }
            p=(p+1)%n; //p往后遍历        
        }
        //退出内层for循环后,p指向m
        while(isOut[p]==true){
            p=(p+1)%n;
        }
        isOut[p]=true;
        cout<<" "<<p+1; //下标从0开始,打印出局的人编号
    }
    return 0;
}

矩阵对角线操作

已知一个6*6的矩阵（方阵），把矩阵二条对角线上的元素加上10，然后输出这个新矩阵。输出得到的新矩阵，注意每个元素占5个长度。

#include
using namespace std;
int main(){
    int q[7][7]; //从下标1开始存，则开数组要多开一维
    for(int i=1;i<=6;i++){
        for(int j=1;j<=6;j++){
            cin>>q[i][j];
        }
    }
    for(int i=1;i<=6;i++){
        for(int j=1;j<=6;j++){
            if(i==j){ //副对角线
                q[i][j]+=10;
            }
            if(i+j==7&&i!=j){ //主对角线
                q[i][j]+=10;
            }
        }
    }
    for(int i=1;i<=6;i++){
        for(int j=1;j<=6;j++){
            printf("%5d",q[i][j]);
        }
        cout<<endl;
    }
    return 0;
}

行列式转换

输入一个3*3的矩阵，将矩阵的行列转换。

#include
using namespace std;
int main(){
    int q[4][4],temp[4][4];
    for(int i=1;i<=3;i++){
        for(int j=1;j<=3;j++){ 
            cin>>q[i][j];
            temp[j][i]=q[i][j]; //边读取边转换
        }
    }
    for(int i=1;i<=3;i++){
        for(int j=1;j<=3;j++){
            cout<<temp[i][j]<<' ';
        }
        cout<<endl;
    }
    return 0;
}

蛇形填数

在nn的方阵里填入1,2,3,···，nn，要求填成蛇形。例如n=4时方阵为：

10 11 12 1
9 16 13 2
8 15 14 3
7 6 5 4
上述的方阵中，多余的空格只是为了便于观察规律，不必严格输出。n<=8. 具体格式看下面的样例输出。

#include
#include
#include
using namespace std;
const int N=9;
int a[N][N];
int main(){
    int n;cin>>n;
    int loop=ceil((double)n/2);  //向上取整，填充的圈数
    int cnt=1;
    for(int i=1;i<=loop;i++){
    	//右上到右下
        for(int x=i,y=n-i+1;x<=n-i+1;x++){
            a[x][y]=cnt++;
        }
        //右下到左下
        for(int x=n-i+1,y=n-i;y>=i;y--){
            a[x][y]=cnt++;
        }
        //左下到左上
        for(int x=n-i,y=i;x>=i;x--){
            a[x][y]=cnt++;
        }
        //左上到右上
        for(int x=i,y=i+1;y<=n-i;y++){
            a[x][y]=cnt++;
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            cout<<setw(3)<<a[i][j];
        }
        cout<<endl;
    }
    return 0;
}

数组去重

给定含有n个整数的序列，要求对这个序列进行去重操作。所谓去重，是指对这个序列中每个重复出现的数，只保留该数第一次出现的位置，删除其余位置。

#include
using namespace std;
int map[20000],m=0;
int main(){
    int n;cin>>n;
    int nums[20000],temp[20000];
    for(int i=0;i<n;i++){
        cin>>nums[i];
        map[nums[i]]++;
        if(map[nums[i]]==1){
            temp[m++]=nums[i];
        }
    }
    for(int i=0;i<m;i++){
        cout<<temp[i]<<' ';
    }
    return 0;
}

区间计数-校门外的树

某校大门外长度为L的马路上有一排树，每两棵相邻的树之间的间隔都是1米。我们可以把马路看成一个数轴，马路的一端在数轴0的位置，另一端在L的位置；数轴上的每个整数点，即0，1，2，……，L，都种有一棵树。
由于马路上有一些区域要用来建地铁。这些区域用它们在数轴上的起始点和终止点表示。已知任一区域的起始点和终止点的坐标都是整数，区域之间可能有重合的部分。现在要把这些区域中的树（包括区域端点处的两棵树）移走。你的任务是计算将这些树都移走后，马路上还有多少棵树。

#include
using namespace std;
bool has_tree[10000]; //标记是否有树
int main(){
    int len,num;
    cin>>len>>num;
    for(int i=0;i<=len;i++){
        has_tree[i]=true; //初始化每个位置都有树
    }
    for(int i=0;i<num;i++){
        int start,end;
        cin>>start>>end;
        for(int j=start;j<=end;j++){
            has_tree[j]=false; //该位置移除树
        }
    }
    int cnt=0;
    for(int i=0;i<=len;i++){
        if(has_tree[i]==true){
            cnt++;
        }
    }
    cout<<cnt<<endl;
    return 0;
}

开关灯

假设有N盏灯(N为不大于5000的正整数)，从1到N按顺序依次编号，初始时全部处于开启状态；有M个人(M为不大于N的正整数)也从1到M依次编号。

第一个人(1号)将灯全部关闭，第二个人(2号)将编号为2的倍数的灯打开，第三个人(3号)将编号为3的倍数的灯做相反处理（即将打开的灯关闭，将关闭的灯打开）。依照编号递增顺序，以后的人都和3号一样，将凡是自己编号倍数的灯做相反处理。

请问：当第M个人操作之后，哪几盏灯是关闭的，按从小到大输出其编号，其间用逗号间隔。

#include
#include
using namespace std;
int a[5000]; //1表示关闭，0表示开启
int main(){
    int n,m;
    cin>>n>>m;
    memset(a,0,sizeof a);
    for(int i=1;i<=m;i++){ //遍历每个人
        for(int j=1;j<=n;j++){ //遍历每盏灯
            if(j%i==0)a[j]=!a[j]; //a[j]初始为0,第一轮循环a[1~n]全为1,用1表示关闭
        }
    }
    for(int j=1;j<=n;j++){
        if(a[j]){ //1表示关闭
            if(j==1)cout<<j;
            if(j!=1)cout<<","<<j;
        }
    }
    return 0;
}

铺地毯

一共有n 张地毯，编号从1 到n。现在将这些地毯按照
编号从小到大的顺序平行于坐标轴先后铺设，后铺的地毯覆盖在前面已经铺好的地毯之上。地毯铺设完成后，组织者想知道覆盖地面某个点的最上面的那张地毯的编号。

#include
using namespace std;
int x0[1000],y0[1000],len[1000],wid[1000];
int main(){
    int n;cin>>n;
    for(int i=1;i<=n;i++){
        cin>>x0[i]>>y0[i]>>len[i]>>wid[i]; //左下角下标和长宽
    }
    int x,y;
    cin>>x>>y;
    for(int i=n;i>=1;i--){ //倒着判断
        if(x>=x0[i]&&x<=(x0[i]+len[i])&&y>=y0[i]&&y<=(y0[i]+wid[i])){
            cout<<i<<endl;
            return 0; 
        }
    }
	cout<<"-1"<<endl;
}

计算鞍点

给定一个5*5的矩阵，每行只有一个最大值，每列只有一个最小值，寻找这个矩阵的鞍点。
鞍点指的是矩阵中的一个元素，它是所在行的最大值，并且是所在列的最小值。

#include
#include
#include
using namespace std;
const int INF=0x3f3f3f3f;
int matrix[5][5],max_row[5],min_col[5];
int main(){
    for(int i=0;i<5;i++){
        min_col[i]=INF; //注意最小值要初始化为大数
    }
    for(int i=0;i<5;i++){
        for(int j=0;j<5;j++){
            cin>>matrix[i][j];
        }
    }
    for(int i=0;i<5;i++){
        for(int j=0;j<5;j++){
            max_row[i]=max(max_row[i],matrix[i][j]);
        }
    }
    for(int j=0;j<5;j++){
        for(int i=0;i<5;i++){
            min_col[j]=min(min_col[j],matrix[i][j]);
        }
    }
    bool found=false;
    int point=0,x=0,y=0;
    for(int i=0;i<5;i++){
        for(int j=0;j<5;j++){
            if(matrix[i][j]==max_row[i] && matrix[i][j]==min_col[j]){
                point=matrix[i][j];
                x=i,y=j;
                found=true;
                break;
            }
        }
    }
    if(found){
        cout<<x+1<<' '<<y+1<<' '<<point<<endl;
    }else{
        cout<<"not found"<<endl;
    }
     
    return 0;
}

矩阵乘法

计算两个矩阵的乘法。n×m阶的矩阵A乘以m×k阶的矩阵B得到的矩阵C 是n×k阶的C矩阵,输入第一行为n, m,
k，表示A矩阵是n行m列，B矩阵是m行k列，n, m, k均小于100。 然后先后输入A和B两个矩阵，A矩阵n行m列，B矩阵m行k列

#include
using namespace std;
const int N=105;
int A[N][N],B[N][N],C[N][N];
int n,m,k;
int main(){
    cin>>n>>m>>k;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            cin>>A[i][j];
        }
    }
    for(int i=1;i<=m;i++){
        for(int j=1;j<=k;j++){
            cin>>B[i][j];
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=k;j++){
            for(int k=1;k<=m;k++){
                C[i][j]+=A[i][k]*B[k][j];
            }
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=k;j++){
            cout<<C[i][j]<<' ';
        }
        cout<<endl;
    }
    return 0;
}

字符串

取出多余的空格

1. 利用scanf循环读取，跳过空格，读一个打印一个

#include
using namespace std;
int main(){
    char s[200];
    while(scanf("%s",&s)==1){
        printf("%s ",s);
    }
    return 0;
}

2. 设置空格标记，遇到连续空格暂停复制

#include
#include
using namespace std;
char str[200],temp[200];
int start,cnt_blank;
int main(){
    cin.getline(str,200);
    for(int i=0;i<=strlen(str);i++){
        if(str[i]==' '){
            cnt_blank++;
            if(cnt_blank==1){
                temp[start++]=str[i];
            }
        }else{
            cnt_blank=0;
            temp[start++]=str[i];
        }
    }
    cout<<temp;
    return 0;
}

字符串移位包含

对于一个字符串来说，定义一次循环移位操作为：将字符串的第一个字符移动到末尾形成新的字符串。
给定两个字符串s1和s2，要求判定其中一个字符串是否是另一个字符串通过若干次循环移位后的新字符串的子串。例如CDAA是由AABCD两次移位后产生的新串BCDAA的子串，而ABCD与ACBD则不能通过多次移位来得到其中一个字符串是新串的子串。

#include
using namespace std;
int main(){
    char s1[40];
    char s2[40];
    char s3[40]; //用于连接a
    char tp[50]; //用于交换
    cin>>s1>>s2;
    if(strlen(s1)<strlen(s2)){
        strcpy(tp,s1);
        strcpy(s1,s2);
        strcpy(s2,tp);
    }
   
    strcpy(s3,s1);
    if(strstr(strcat(s1,s3),s2)==NULL)cout<<"false";
    else cout<<"true";
    return 0;
}

打印输出

输入n个数，要求程序按输入时的逆序把这n个数打印出来，已知整数不超过100个。也就是说，按输入相反顺序打印这n个数。

#include
#include
using namespace std;
int main(){
    char a[100];
    cin.getline(a,100); //读取一整行，逆序输出
    int len_a=strlen(a);
    for(int i=len_a-1;i>=0;i--){
        cout<<a[i]; //不用加空格
    }
    return 0;
}

字符串判等

判断两个由大小写字母和空格组成的字符串在忽略大小写，且忽略空格后是否相等。

#include
#include
using namespace std;
bool check_equal(char a[],char b[]){
    int lena=strlen(a),lenb=strlen(b);
    if(lena!=lenb){
        return false;
    }
    for(int i=0;i<lena;i++){
        if(a[i]!=b[i]){
            return false;
        }
    }
    return true;
}
char str1[100],str2[100];
char temp1[100],temp2[100];
int main(){ 
    cin.getline(str1,100);
    cin.getline(str2,100);
    int m=0,n=0;
    for(int i=0;i<strlen(str1);i++){
        if(str1[i]!=' '){
            if(str1[i]>='a' && str1[i]<='z'){
                temp1[m++]=str1[i];
            }else{
                temp1[m++]=str1[i]+32; //大小写字母相差32
            }
        }
    }
    for(int i=0;i<strlen(str2);i++){
        if(str2[i]!=' '){
            if(str2[i]>='a' && str2[i]<='z'){
                temp2[n]=str2[i];
                n++;
            }else{
                temp2[n]=str2[i]+32;
                n++;
            }
        }
    }
    if(check_equal(temp1,temp2)){
        cout<<"YES"<<endl;
    }else{
        cout<<"NO"<<endl;
    }
    return 0;
    
}

统计单词长度

输入一行单词序列，相邻单词之间由1个或多个空格间隔，请对应地计算各个单词的长度。注意:如果有标点符号(如连字符，逗号)，标点符号算作与之相连的词的一部分。没有被空格间开的符号串，都算作单词。

#include
#include
using namespace std;
int f=1;
char str[50];
int main(){
    while(cin>>str){ //利用cin分割空格，计算长度
        if(f==1)f=0;
        else cout<<",";
        
        cout<<strlen(str);
    }
    return 0;
}

哈希

平台最大长度

已知一个已经从小到大排序的数组，这个数组的一个平台（Plateau）就是连续的一串值相同的元素，并且这一串元素不能再延伸。例如，在
1，2，2，3，3，3，4，5，5，6中1，2-2，3-3-3，4，5-5，6都是平台。试编写一个程序，接收一个数组，把这个数组最长的平台找出
来。

#include
using namespace std;
int map[1000]; //放main函数外面，否则初始值不是0
int main(){
    int n;cin>>n;
    int nums[1000];
    for(int i=0;i<n;i++){
        cin>>nums[i];
        map[nums[i]]++; //映射
    }
    int max_len=-1000;
    for(int i=0;i<n;i++){
        max_len=max(map[nums[i]],max_len);
    }
    cout<<max_len<<endl;
    return 0;
}

统计数字出现次数

给定一个非负整数数组，统计里面每一个数的出现次数。我们只统计到数组里最大的数。

假设Fmax（Fmax<10000）是数组里最大的数，那么我们只统计{0,1,2…Fmax}里每个数出现的次数,按顺序输出。

#include
#include
using namespace std;
int nums[10000];
int map[10000];
int main(){
    int n;cin>>n;
    for(int i=0;i<n;i++){
        cin>>nums[i];
        map[nums[i]]++;
    }
    int max_value=-1000;
    for(int i=0;i<n;i++){
        max_value=max(max_value,nums[i]);
    }
    for(int i=0;i<=max_value;i++){
        cout<<map[i]<<endl;
    }
    return 0;
}

第一次只出现一次的字符

给定一个只包含小写字母的字符串，请你找到第一个仅出现一次的字符。如果没有，输出no。

#include
#include
using namespace std;
char str[100010];
int map_cnt[26];
int main(){
    cin.getline(str,100010);
    for(int i=0;i<strlen(str);i++){
        map_cnt[str[i]]++;
    }
    for(int i=0;i<strlen(str);i++){ //按照原字符串顺序，输出第一个1
        if(map_cnt[str[i]]==1){
            cout<<str[i]<<endl;
            return 0;
        }
    }
    cout<<"no"<<endl;
    return 0;
}

递归

fibo

输入n，输出fiob前n项

#include
using namespace std;
const int N=1010;
int fibo[N];
int main(){
	int n;
	cin>>n;
	fibo[1]=1;
	fibo[2]=1;
	for(int i=2;i<=n;i++){
		fibo[i]=fibo[i-1]+fibo[i-2];
	}
	for(int i=1;i<=n;i++){
		cout<<fibo[i]<<' ';
	}
	return 0;
}

阶乘

#include
using namespace std;
const int N=1010;
int fact(int n){
	if(n<=1)return 1;
	return n*fact(n-1);
}
int main(){
	int n;cin>>n;
	cout<<fact(n)<<' ';
	return 0; 
}

24点

输入四个整数，判断能否通过+ - * / 得到24

#include
using namespace std;
const int N=1010;
int A[N],n,a,b;
bool judge24(int A[],int n){ 
	if(n==1)return A[0]==24; //四个数合并为一个数，判断结果是否=24
	for(int i=0;i<n;i++){
		for(int j=i+1;j<n;j++){
			a=A[i],b=A[j];
			A[j]=A[n-1];  //最后一个数覆盖j的位置上的数
			A[i]=a+b; //合并i j的数结果保存到i
			if(judge24(A,n-1))return true;
			A[i]=a-b; //减
			if(judge24(A,n-1))return true;
			A[i]=b-a; //减
			if(judge24(A,n-1))return true;
			A[i]=a*b; //乘
			if(judge24(A,n-1))return true;
			if(b!=0 && a%b==0){
				A[i]=a/b; //除
				if(judge24(A,n-1))return true;
			}
			if(a!=0 && b%a==0){
				A[i]=b/a; //除
				if(judge24(A,n-1))return true;
			}
			A[i]=a,A[j]=b; //回溯
		}
	}
	return false;
}
int main(){
	int a,b,c,d;
	n=4;
	while(cin>>a>>b>>c>>d){
		A[0]=a,A[1]=b,A[2]=c,A[3]=d;
		if(judge24(A,n)==true)cout<<"true"<<endl;
		else cout<<"false"<<endl; 
	}
	return 0;
	
}

全排列

输入n，按照字典序输出1~n的全排列

#include
using namespace std;
const int N=1010;
int n;
int path[N];
bool used[N];
void dfs(int u){
	if(u>n){
		for(int i=1;i<=n;i++){
			cout<<path[i]<<" ";
		}
		cout<<endl;
	}
	for(int i=1;i<=n;i++){
		if(!used[i]){
			path[u]=i; 
			used[i]=true;
			dfs(u+1);
			used[i]=false;
		}
	}
}
int main(){
	cin>>n;
	dfs(1);
	return 0;
}

函数表达式求值

double f(double n,double x){
    if(n==0)return 1;
    else return x/(n+f(n-1,x));
}
int main(){
    double x,n;
    cin>>x>>n;
    printf("%.2lf",f(n,x));
    return 0;
}

Function F_x satisfies:
F_(0) = sin{n}
F_(x) = sin{F_(x-1)} (x>0)
Calculate F_(n).

double f(double x,double n){ //x代表递归次数
	if(x==0)return sin(n);
	return sin(f(x-1,n));
}
int main(){
	double n;
	cin>>n;
	printf("%.6lf",f(n,n)); //n次递归
    return 0;
}

Function F_x satisfies:
F_0 = cos{n}
F_x = cosF_{x-1} (x>0)
Calculate F_n.

输入格式 0<=n<=10^30.

int main(){
    char a[100];
    while(scanf("%s",&a)!=EOF){ //字符数组读取长大数字
        if(strlen(a)<=3){ 
            int shuzi=atoi(a); //转化为整数
            double x=cos(shuzi); 
            while(shuzi--){ //迭代次数
                x=cos(x);
            }
            printf("%.6lf\n",x);
        }else{
            printf("0.739085\n");
        }
    }
    return 0;
}

约瑟夫环

n个人围一圈,从1开始按顺序报数，报到m的人出圈,计算最后留下的人编号.

1. vector模拟法:
   使用迭代器it遍历容器,cnt作为计数器
   当cnt==m时，从容器中移除it指向的对象，同时cnt归位
   否则it++,遇到队尾就回到队头

//约瑟夫环 
#include
#include
#include
using namespace std;

int main(){
	int T;
	cin>>T;
	while(T--){
		vector<int>v;
		int n,m;
		cin>>n>>m;
		//赋值初始化容器 
		for(int i=1;i<=n;i++)v.push_back(i);
		vector<int>::iterator it=v.begin();
		int cnt=1;
		while(v.size()>1){
			if(cnt==m){
				it=v.erase(it); //移除
				if(it==v.end())it=v.begin(); 
				cnt=1; //重置计数器 
			}else{
				it++;
				if(it==v.end())it=v.begin();
				cnt++; //计数器递增 
			}
		}
		cout<<v[0]<<endl;
	}
	return 0;
}

2. 递归法

旧编号:1 2 3 … m-1 m m+1 m+2
新编号:…m-1 1 2
old 与 new 的关系:old=(new+m-1)%n+1

使用f(n,m)表示n个人报数m的人离开最后剩余的人:
递归关系:f(n,m)=(f(n-1,m)+m-1)%n+1

#include
using namespace std;
int f(int n,int m){
	return n==1?n:(f(n-1,m)+m-1)%n+1;
}
int main(){
	int T;
	cin>>T;
	while(T--){
		int n,m;
		cin>>n>>m;
		cout<<f(n,m)<<endl;
	}
	return 0;
}
		

栈

入栈顺序

//入栈顺序 
#include
#include
using namespace std;
int main(){
	int T;
	cin>>T;
	while(T--){
		stack<int>s;
		bool isOK=true;
		int n;
		int data=1;
		cin>>n; //1~n的顺序入栈，出栈顺序不定
		for(int i=1;i<=n;i++){
			int t;
			cin>>t; //挨个读取要检测的出栈数据
			while(data<=t)s.push(data++); //入栈
			if(s.top()==t)s.pop(); //出栈
			else isOK=false;
		}
		cout<<(isOK?"YES":"NO")<<endl;
	}
	return 0;
}

括号匹配

1. 左括号入栈

#include
#include
#include
using namespace std;
char str[200];

bool isMatch(char str[]){
	stack<char>s;
	for(int i=0;i<strlen(str);i++){
		if(str[i]=='('){
			s.push(str[i]);	
		}else{
			if(s.empty()){ //栈提前为空,没有匹配的括号,返回false 
				return false;
			}else{
				if(s.top()=='('){
					s.pop();
				}else return false;				
			}
		}
	}
	return s.empty();
}
int main(){
	while(cin>>str){
		if(isMatch(str)){
			cout<<"YES"<<endl;
		}else{
			cout<<"NO"<<endl;
		}
	}
	return 0; 
}

2. 右括号入栈

#include
#include
#include
using namespace std;

bool isMatch(char str[]){
	if(strlen(str)%2!=0)return false;
	stack<char>stk;
	for(int i=0;i<strlen(str);i++){
		if(str[i]=='(')stk.push(')');
		else if(str[i]=='[')stk.push(']');
		else if(str[i]=='{')stk.push('}');
		else if(stk.empty() || stk.top()!=str[i])return false;
		else stk.pop(); 
	}
	return stk.empty();
}
int main(){
	int T;
	cin>>T;
	while(T--){
		char str[200];
		cin>>str;
		if(isMatch(str))cout<<"true"<<endl;
		else cout<<"false"<<endl;
	}
	return 0;
}

括号匹配的最小数量

#include
using namespace std;
int dp[101][101]; //dp[i][j]表示str[i~j]能匹配括号的最大数量 

int main(){
    int T;
    cin>>T;
    while(T--){
        char str[1001];
        scanf("%s",str+1);
        int len=strlen(str+1);
        int res=len;
        memset(dp,0,sizeof dp);
 
        for(int l=2;l<=len;l++){
            for(int i=1;i<=len;i++){
                int j=l+i-1;
                if(j>len)break; 
                if(str[i]=='('&&str[j]==')' ||str[i]=='[' &&str[j]==']'){
                    dp[i][j]=dp[i+1][j-1]+2; //i~j比i+1~j-1多匹配两个 
                }
                //区间划分:
				//i~j能匹配的最大数量=i~k匹配的最大数量+i~j匹配的最大数量 
                for(int k=i;k<j;k++){
                    dp[i][j]=max(dp[i][j],dp[i][k]+dp[k][j]);
                }
            }
        }
        res-=dp[1][len]; //总的括号数减去最大匹配数即为需要添加的最少个数
        cout<<res<<endl;
    }
    return 0;
}