Parity game POJ1733(并查集边带权或扩展域)

题干：
小A和小B玩游戏，小A写了一个长度为N的01序列，小B向小A提出许多问题，每个问题，小B指定两个数L和R，小A回答区间中有奇数个1还是偶数个1，小B发现小A可能在撒谎，向你求助，
求出一个最小的K，满足存在01序列满足1~k组询问，不满足第K加一组询问，M<=10000 N<=10⁹
Sample Input
10
5
1 2 even
3 4 odd
5 6 even
1 6 even
7 10 odd
Sample Output
3
题意: 输入n表示有一个长度为n的0,1字符串, m表示接下来有m行输入, 接下来的m行输入中x, y, even表示第x到第y个字符中间1的个数为偶数个, x, y, odd表示第x到第y个字符中间1的个数为奇数个, 若m句话中第k+1是第一次与前面的话矛盾, 输出k;

思路：
这道题可以用带权并查集和扩展域并查集两种方法做，这里两种方法都讲一下吧

首先讲带权并查集的思路。
因为题目要求的是奇偶性，可知，一个01数列中从第l个元素到第r个元素之间有奇数个1，如果令sum[]为前缀和，则等价于sum[l-1]^ sum[r]=1;偶数个1的情况就是sum[l-1]^sum[r]=0;这个应该不难理解。当然这个题目中我们不需要求出sum[]具体是多少，只需要知道它们之间的关系就行了。

sum[l-1]^ sum[r]=1;这个式子表示，如果在[l,r]中有奇数个1，表示sum[l-1]和sum[r]奇偶性不同，并不需要真正求出sum[]的值，只是把sum看作变量，类型程序自动分析。假如l-1前面有奇数个1，就用sum[l-1]=1来表示，有偶数个1就用sum[l-1]=0来表示。

sum[l,r]有奇数个1，转化为sum[l-1]和sum[r]奇偶性不同，既然奇偶性不同，sum[l-1]、sum[r]其中一个是1，一个是0，所以用异或操作就可以，最终转化为sum[l-1]^ sum[r]=1。

由于数据范围，需离散化

有了上述的理解，我们使用“边带权”并查集，来处理多种传递关系。

边权d[x]为0，表示x与fa[x]奇偶性相同；为1，表示x与fa[x]奇偶性不同。在路径压缩时，对x到树根路径上的所有边权左异或运算，即可得到x与树根的奇偶性关系。

对于输入的每个问题，设在离散化后l-1和r的值分别为x和y，用ans表示该问题的回答（0代表偶数个1，1代表奇数）

先检查x和y是否在同一个集合（奇偶关系是否已知).get(x)、get(y)后d[x] xor d[y]即为x和y的奇偶性，如下图

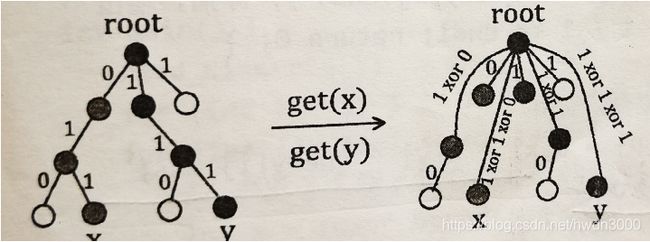
因为在同一个集合，x和y有共同的树根，假如x和树根的奇偶性相同，y和树根的奇偶性相同，那么x和y的奇偶性就相同。
x和y的奇偶性可以通过树根（也就是并查集集合代表传递。
假如x和y不在同一集合
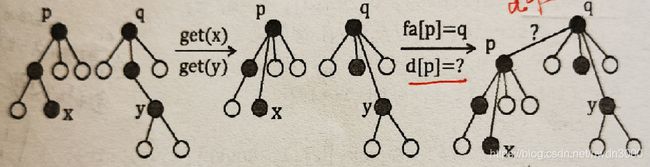
get（x）的树根是p d[x]表示x节点和p节点的奇偶性
get（y）的树根是q d[y]表示y节点和q节点的奇偶性
p和q节点的之间的关系不知道，把p合并到q，求出p到q的边权
d[p],那么x和y的奇偶性就可以传递出来
d[x] x到p的关系
d[p] p到q的关系
d[y] y到q的关系
d[x] ^ d[p] ^d[y]就是x和y的关系
怎么求d[p],看下图

例如样例输入 5 6 even
我下面的代码
5 存在x中 ，6 存在y 中，奇偶性存在query[i].ans中
如果x和y的树根不在一个集合中，表示[5,6]这段区域和其他的输入区域没有交集，不能判断出说的是真是假，题目是要求是至少多少个回答之后可以确定A一定在撒谎。这样的不能判断，就继续往下判断，但这个时候可以根据这个输入，求出d[p]以备以后用到

query[i].ans=d[x] ^ d[y] ^d[p] ,
d[p]=d[x]^ d[y] ^query[i].ans

并查集边带权完整代码

#include
#include
#include
#include
#include
using namespace std;
struct { int l, r, ans; } query[10010];
int a[20010], fa[20010], d[20010], n, m, t;
void read_discrete() { // 读入、离散化
 cin >> n >> m;
 for (int i = 1; i <= m; i++) {
  char str[5];//输入格式5 6 even
  scanf("%d%d%s", &query[i].l, &query[i].r, str);
  query[i].ans = (str[0] == 'o' ? 1 : 0);
  a[++t] = query[i].l - 1;//转化为l-1变量
  a[++t] = query[i].r;//转化为r变量
 }
 sort(a + 1, a + t + 1);
 n = unique(a + 1, a + t + 1) - a - 1;
}
int get(int x) {
 if (x == fa[x]) return x;
 int root = get(fa[x]);
 d[x] ^= d[fa[x]];
 return fa[x] = root;
}
int main() {
 read_discrete();
 for (int i = 1; i <= n; i++) fa[i] = i;
 for (int i = 1; i <= m; i++) {
  // 求出l-1和r离散化之后的值
  int x = lower_bound(a + 1, a + n + 1, query[i].l - 1) - a;
  int y = lower_bound(a + 1, a + n + 1, query[i].r) - a;
  // 执行get函数，得到树根，并进行路径压缩
  int p = get(x), q = get(y);
  if (p == q) { // 已经在同一集合内
   if ((d[x] ^ d[y]) != query[i].ans) { // 矛盾，输出
    cout << i - 1 << endl;
    return 0;
   }
  }
  else { // 不在同一集合，合并
   fa[p] = q;
   d[p] = d[x] ^ d[y] ^ query[i].ans;
  }
 }
 cout << m << endl; // 没有矛盾
}

第二种解决方案就是使用“扩展域”的并查集。
这种方法我个人觉得会比较好理解。基本思路也是和上面一样用前缀和之间的关系来判断。把每个变量x变成两个：x_odd和x_even，也就是奇偶两种情况。对于每一个询问，用0代表偶数，1代表奇数，那么对于每个询问只有以下情况
　
　 询问为0：判断x_odd与y_even是否在同一集合中（或者判断x_even和y_odd也一样，都是等价的，原因后面会说），如果在同一集合，则矛盾，直接输出答案;
　 否则，合并x_odd与y_odd，x_even与y_even，表示sum[x]与sum[y]同奇偶。
　　
　询问为1：判断x_odd与y_odd是否在统一集合中（当然判断x_even与y_even也一样），如果在同一集合，则矛盾，直接输出答案;
　 否则，合并x_odd与y_even，x_even与y_odd，表示sum[x]与sum[y]异奇偶。
　
　 原理：输入的询问告诉两个变量的奇偶性相同，假如询问为0时，那也就是x_odd与y_odd可以互相推出，其中一个是偶，另一个也是偶，同理x_even与y_even也可以互相推出，它们是等价的信息，也就是x_odd与y_odd在同一集合中，同理x_even与y_even在同一集合中。所以如果询问0，先判断x_odd和y_even或x_even和y_odd是不是在同一集合，在就错了，不在，就把x_odd与y_odd合并一个集合，把x_even与y_even也合并为一个集合。
上述合并的同时还维护了关系的传递性，试想在处理完（x，y，0）和（y，z，1）这两个回答后，x和z的关系就已知了，这种做法相当于在无向图上维护节点之间的连通情况，只是扩展了多个域来应对多种传递关系。
在处理每个问题之前，我们当然也要先检查是否存在矛盾。若两个变量x和y对应的x_odd和y_odd节点在同一个集合内，则已知二者奇偶性相同。若两个变量x和y对应的x_odd和y_even节点在同一个集合内，则已知二者奇偶性不同。
完整代码：

// POJ1733 扩展域并查集做法
#include
#include
#include
#include
#include
using namespace std;
struct { int l, r, ans; } query[10010];
int a[20010], fa[40010], n, m, t;
void read_discrete() { // 读入、离散化
 cin >> n >> m;
 for (int i = 1; i <= m; i++) {
  char str[5];
  scanf("%d%d%s", &query[i].l, &query[i].r, str);
  query[i].ans = (str[0] == 'o' ? 1 : 0);
  a[++t] = query[i].l - 1;
  a[++t] = query[i].r;
 }
 sort(a + 1, a + t + 1);
 n = unique(a + 1, a + t + 1) - a - 1;
}
int get(int x) {
 if (x == fa[x]) return x;
 return fa[x] = get(fa[x]);
}
int main() {
 read_discrete();
 for (int i = 1; i <= 2 * n; i++) fa[i] = i;
 for (int i = 1; i <= m; i++) {
  // 求出l-1和r离散化之后的值
  int x = lower_bound(a + 1, a + n + 1, query[i].l - 1) - a;
  int y = lower_bound(a + 1, a + n + 1, query[i].r) - a;
  int x_odd = x, x_even = x + n;
  int y_odd = y, y_even = y + n;
  if (query[i].ans == 0) { // 回答奇偶性相同
   if (get(x_odd) == get(y_even)) { // 与已知情况矛盾
    cout << i - 1 << endl;
    return 0;
   }
   fa[get(x_odd)] = get(y_odd); // 合并
   fa[get(x_even)] = get(y_even);
  }
  else { // 回答奇偶性不同
   if (get(x_odd) == get(y_odd)) { // 与已知情况矛盾
    cout << i - 1 << endl;
    return 0;
   }
   fa[get(x_odd)] = get(y_even); // 合并
   fa[get(x_even)] = get(y_odd);
  }
 }
 cout << m << endl; // 没有矛盾
}