【剑指offer】学习计划day4
![]()
目录
一. 前言
二.数组中重复的数字
a.题目
b.题解分析
c.AC代码
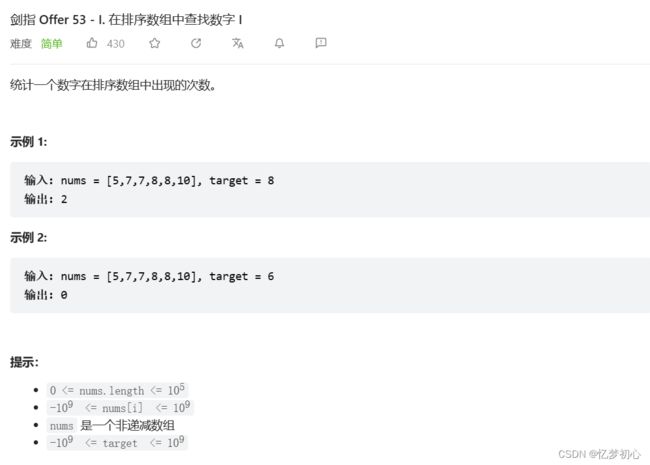
三.在排序数组中查找数字 I
a.题目
b.题解分析
c.AC代码
四.0~n-1中缺失的数字
a.题目
b.题解分析
c.AC代码
一. 前言
本系列是针对Leetcode中剑指offer学习计划的记录与思路讲解。详情查看以下链接:
剑指offer-学习计划https://leetcode.cn/study-plan/lcof/?progress=x56gvoct
本期是本系列的day4,今天的主题是----》查找算法(简单)
题目编号:JZ03,JZ53-I,JZ53-II
二.数组中重复的数字
a.题目
b.题解分析
法1. 暴力排序
我们可以直接对数组从小到大进行排序。然后遍历这个有序数组,如果出现前后两个元素重复的情况,则返回这个数即可。
但是我们知道排序的时间成本太高了,最快也是![]() 量级的,我们有没有办法将时间复杂度降到
量级的,我们有没有办法将时间复杂度降到![]() 呢?
呢?
法2. 哈希表
这种和查找重复元素有关的题目,我们可以使用哈希表,哈希表查找的时间复杂度为O(1)。我们可以在直接遍历数组的同时在哈希表中查找是否存在此元素,如果存在,则该元素就是一个重复元素;如果不存在,则将其插入哈希表。
时间复杂度:遍历数组O(N),哈希表插入和查找都为O(1),合计O(N)。
空间复杂度:使用了哈希表作为辅助空间,空间复杂度为O(N)。
法3. 原地交换
方法二其实就是我们经常采用的以空间换时间的策略。那有没有什么方法既可以保证时间效率,又可以节省空间呢?答案是有的,我们可以在原数组上动刀子
这种方法其实也是利用了哈希映射的思想,我们观察题目发现数组的下标范围为0~n-1,每个元素也在0~n-1之间,因此我们可以将原数组看做一个哈希表来节省空间。具体的方式如下:
- 遍历数组arr,i为下标,如果arr[i] == i,即当前元素的值和其对应的下标相同,说明当前元素已经在正确的索引位置,无需交换,i++向后遍历。
- 当arr[i] != i 时,我们需要将其交换到正确的索引位置。此时如果索引位置处的值等于arr[i],则说明此索引对应多个值,arr[i]就是一组重复数字,返回;否则就将arr[i]交换到索引位置arr[i]处。
- 如果数组遍历完依旧没有返回,则没有重复数字,返回-1。
时间复杂度:遍历一遍数组,时间复杂度为O(N)。
空间复杂度:没有使用额外的辅助空间,空间复杂度为O(N)。
c.AC代码
//法1:暴力排序,不推荐,代码略
//法2:哈希表,时间O(N),空间O(N)
class Solution {
public:
int findRepeatNumber(vector& nums)
{
unordered_map hash; //定义一个哈希表,表中的值表示对应元素是否存在
for (int i = 0; i < nums.size(); i++) //遍历数组
{
if (hash[nums[i]] == true) //当前元素已经存在,直接返回
{
return nums[i];
}
hash[nums[i]] = true; //不存在则插入
}
return -1; //找不到重复元素,返回-1
}
};
//法3:原地交换,时间O(N),空间O(1)
class Solution {
public:
int findRepeatNumber(vector& nums)
{
int i=0;
while(i < nums.size()) //遍历数组
{
if(nums[i] == i) //已经在索引位置上,无需交换,前进
{
i++;
}
else if(nums[ nums[i] ] == nums[i]) //不在索引位置,且索引位置已经有正确值了
{
return nums[i];
}
else //不在索引位置,索引位置不是正确值,交换
{
swap(nums[i],nums[ nums[i] ]);
}
}
return -1; //找不到重复元素,返回-1
}
}; 三.在排序数组中查找数字 I
a.题目
b.题解分析
法1. 遍历计数(极度不推荐)
这种最朴素的解法就不用多说了,遍历数组用变量统计次数,一次循环O(N)搞定!但是如果你这么做的话面试官可能就要开始和你闲聊了,问问你们家乡的风土人情
法2. 两次二分(推荐)
是个排序数组又让我们查找,自然而然我们就会想到二分查找。既然让我们求出现的次数,那我们找到左边界,再找到右边界,两个下标相减不就好了,easy。
具体方法如下:
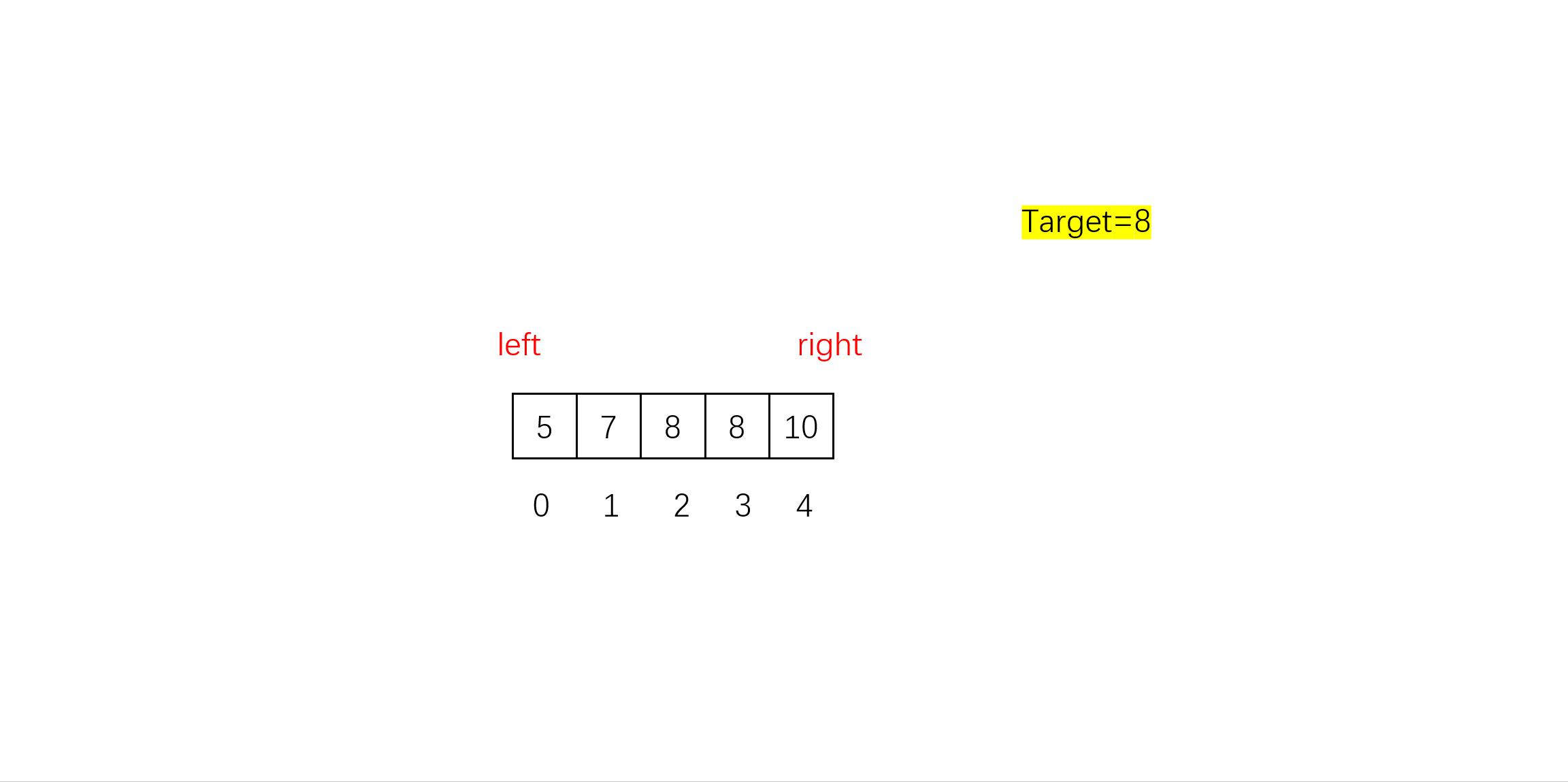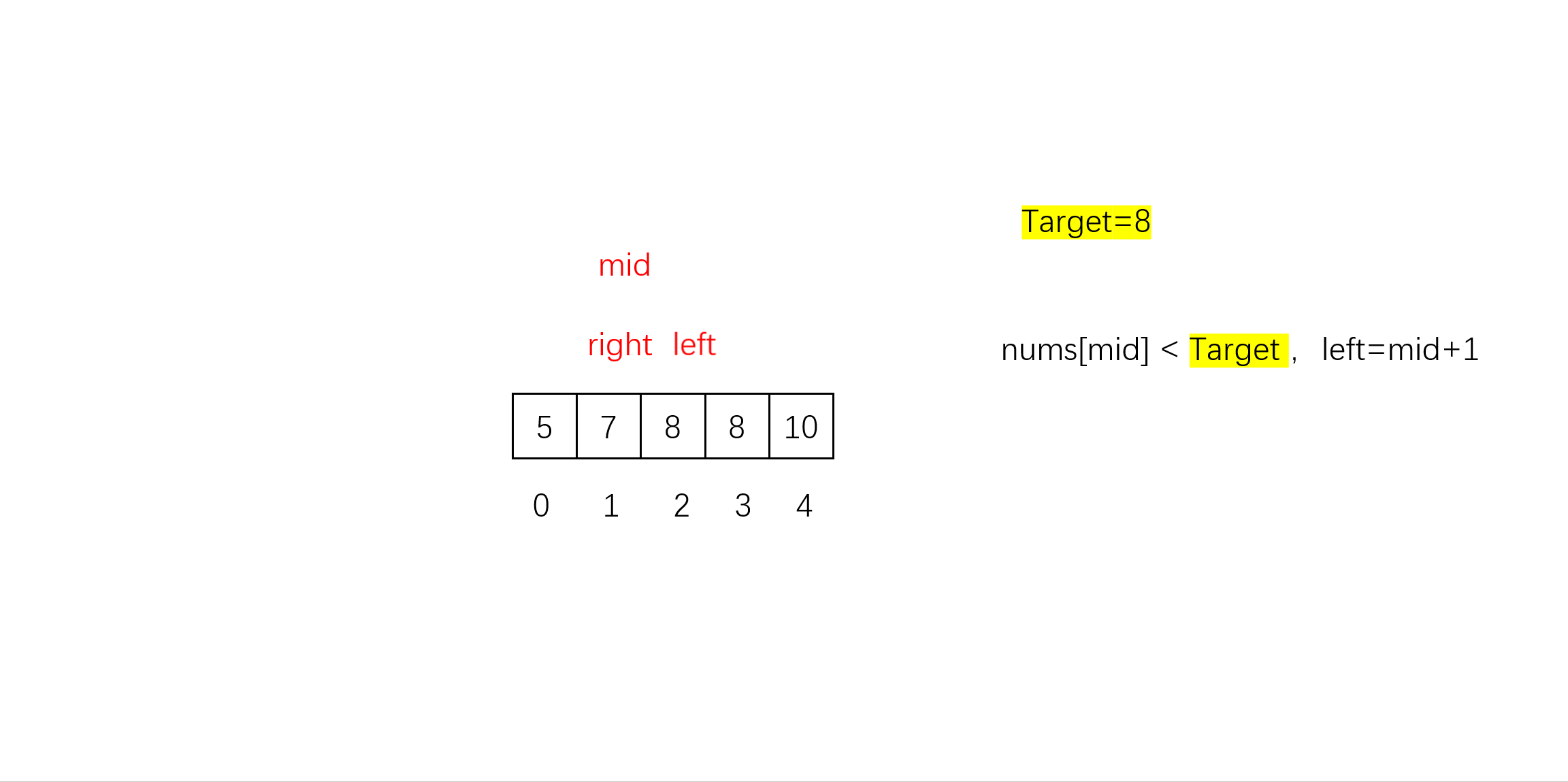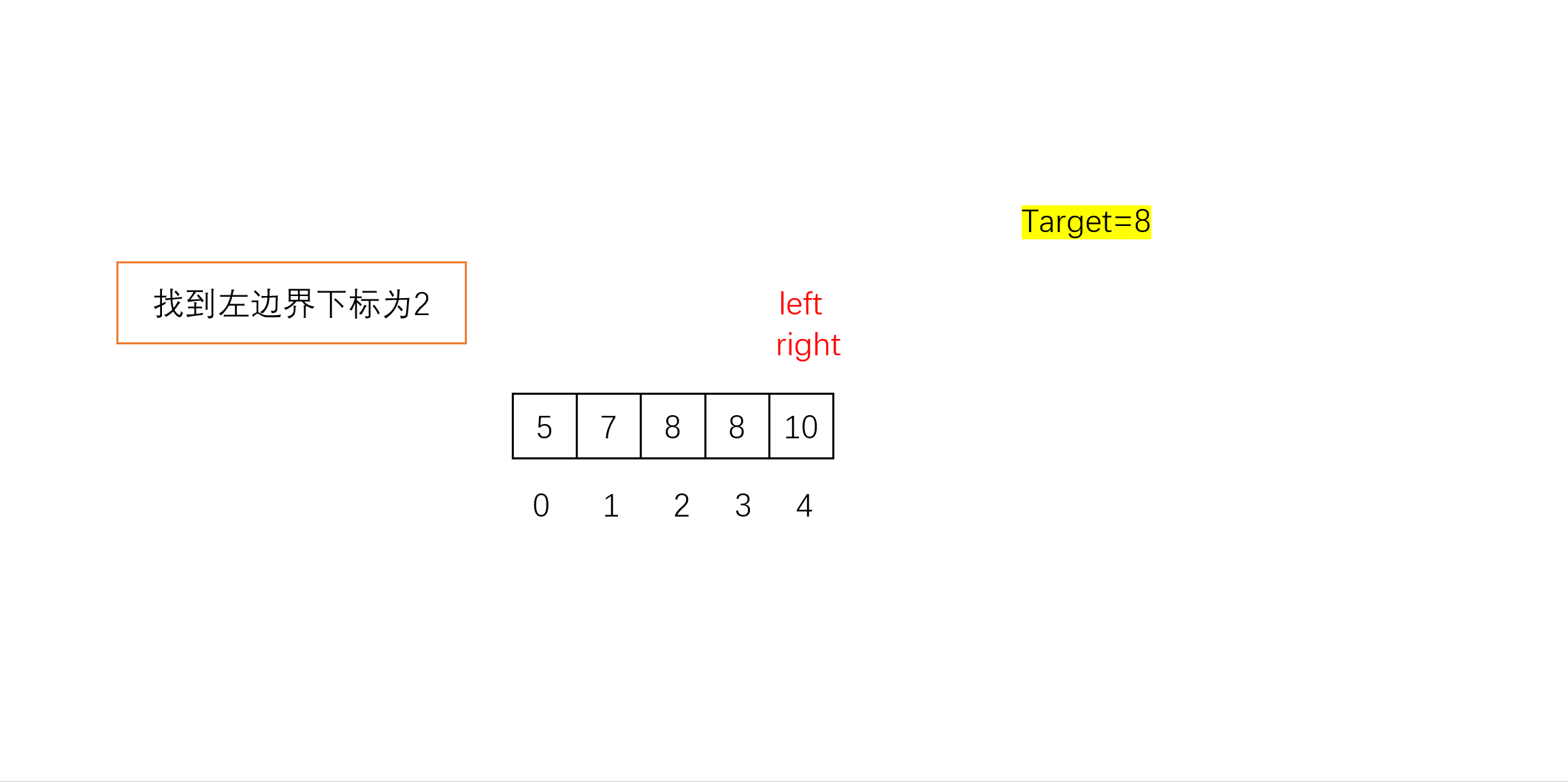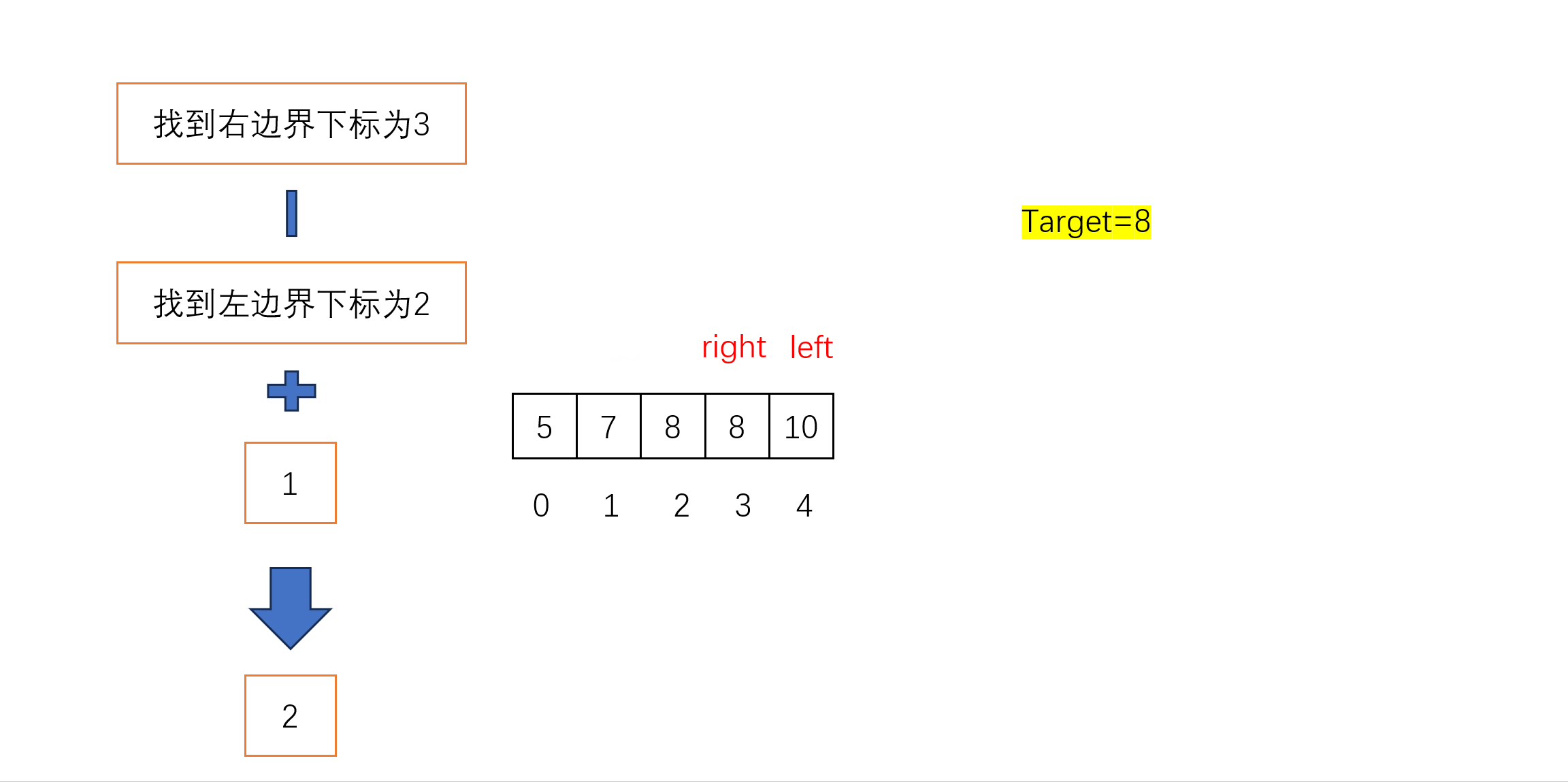
- 初始化:初始化左边界为0,右边界为numsSize-1。即闭区间。
- 找左边界下标:先求出中间下标mid,如果nums[mid] >= target,则缩小右边界right到mid-1,如果nums[mid] < target,则缩小左边界left到mid+1。循环直到left > right时,left就是我们要找的左边界。
- 判断有效性(可选):判断一下找到的左边界是否有效,无效则说明没有此数字,直接返回。
- 找右边界下标:求出中间下标mid,如果nums[mid] <= target,则缩小左边界left到mid+1,如果nums[mid] > target,则缩小右边界right到mid-1。循环直到left > right时,right就是我们要找的右边界。
- 返回区间个数:由于我们的边界是闭区间,所以区间内的元素个数为right-left+1,即为最终答案。
具体动图如下:
时间复杂度:二分法每次搜索区间缩小一半,时间复杂度O(logn)。
空间复杂度:只使用到了常数级的变量,空间复杂度为O(1)。
法3. 一次二分(不太推荐)
上面是分别用2次二分查找左右边界,其实我们也可以只用1次二分同时查找左右边界噢,方法如下:
- 初始化:初始化左边界为0,右边界为numsSize-1。即闭区间。
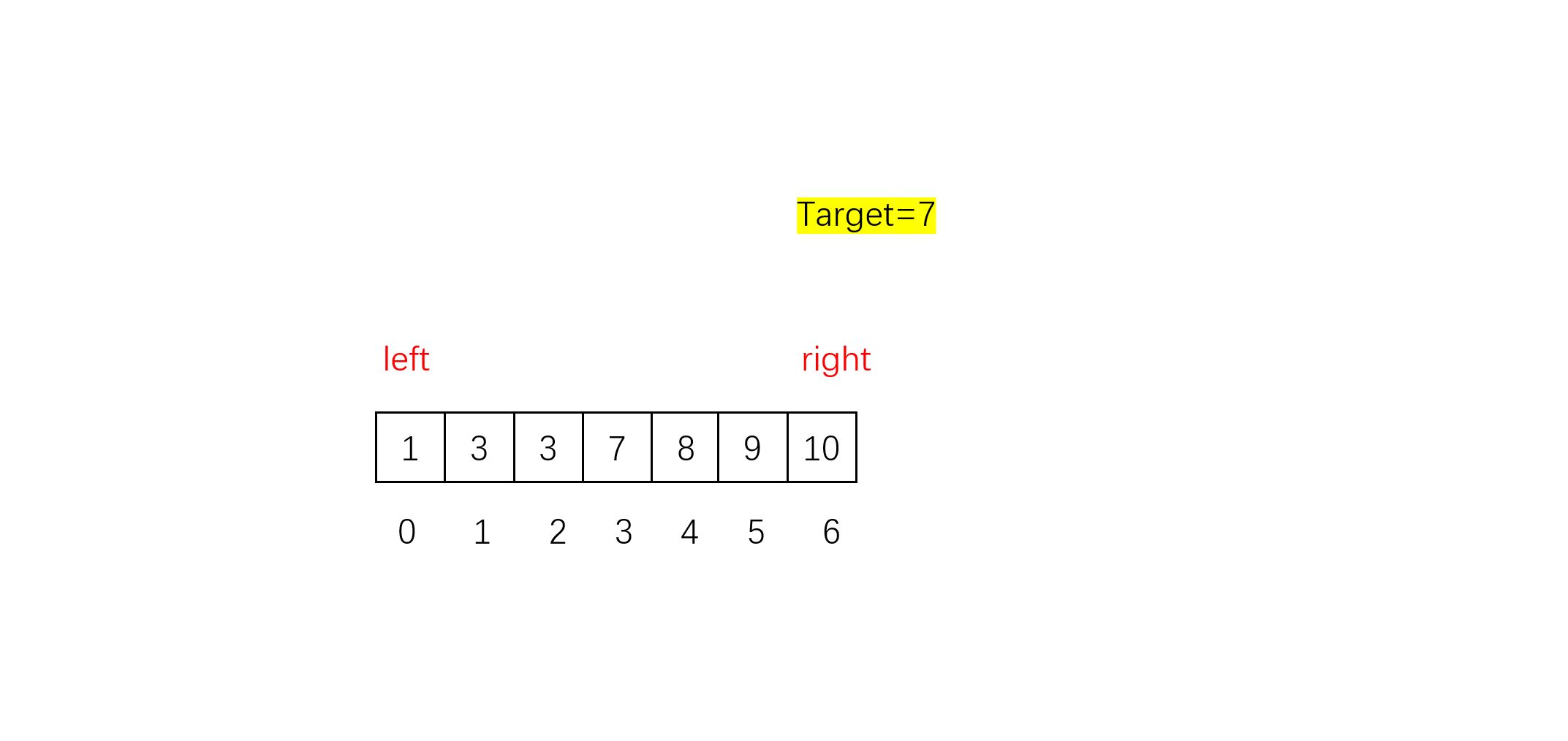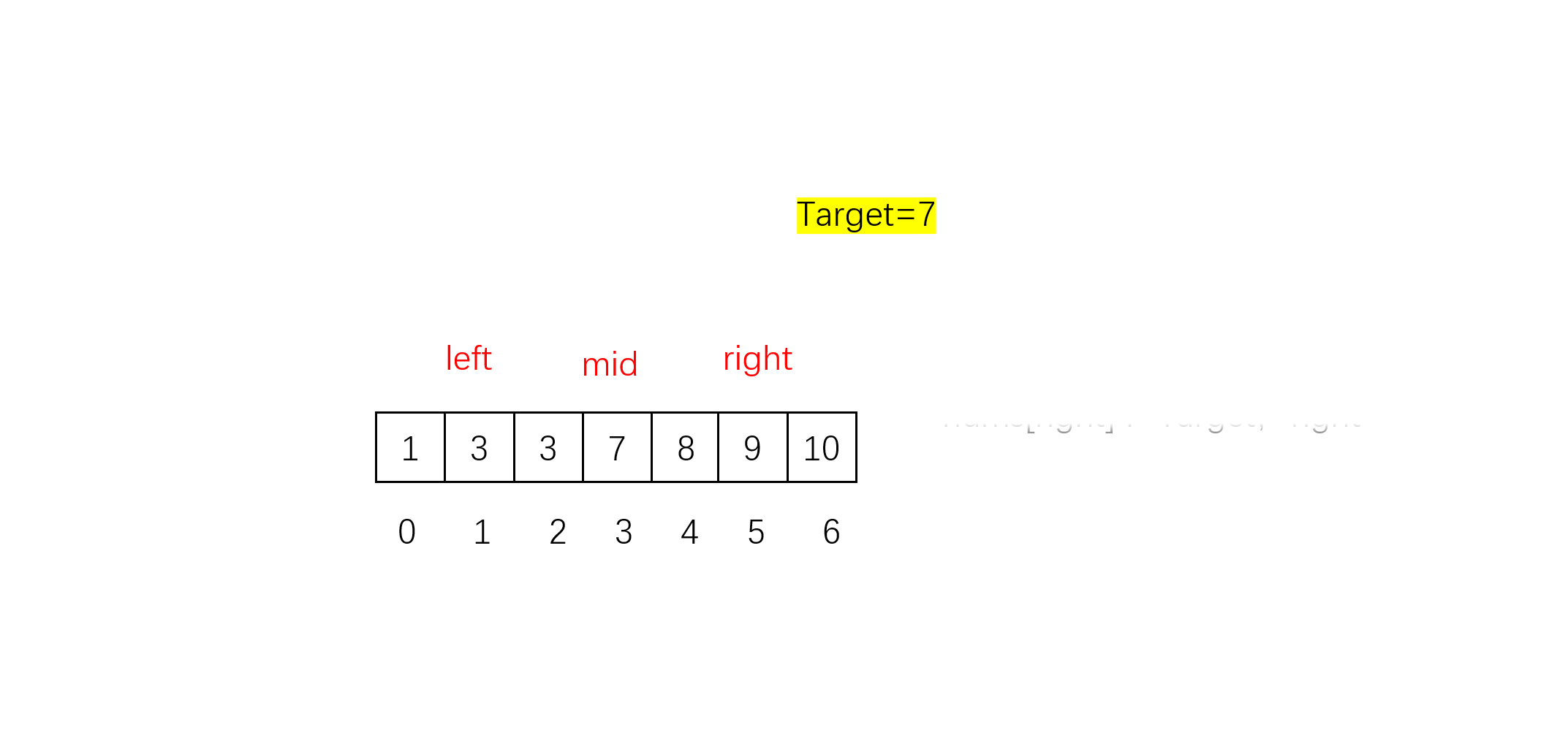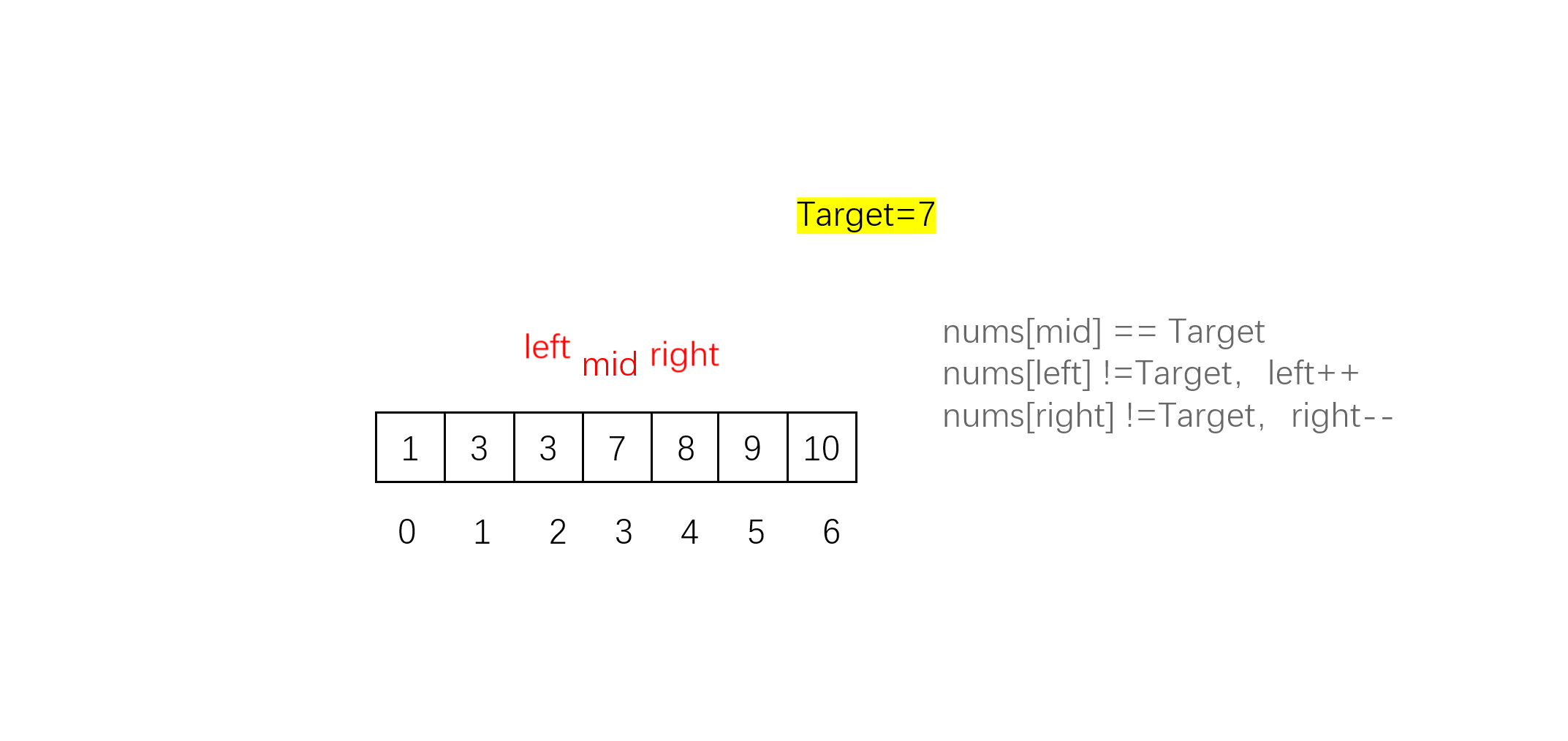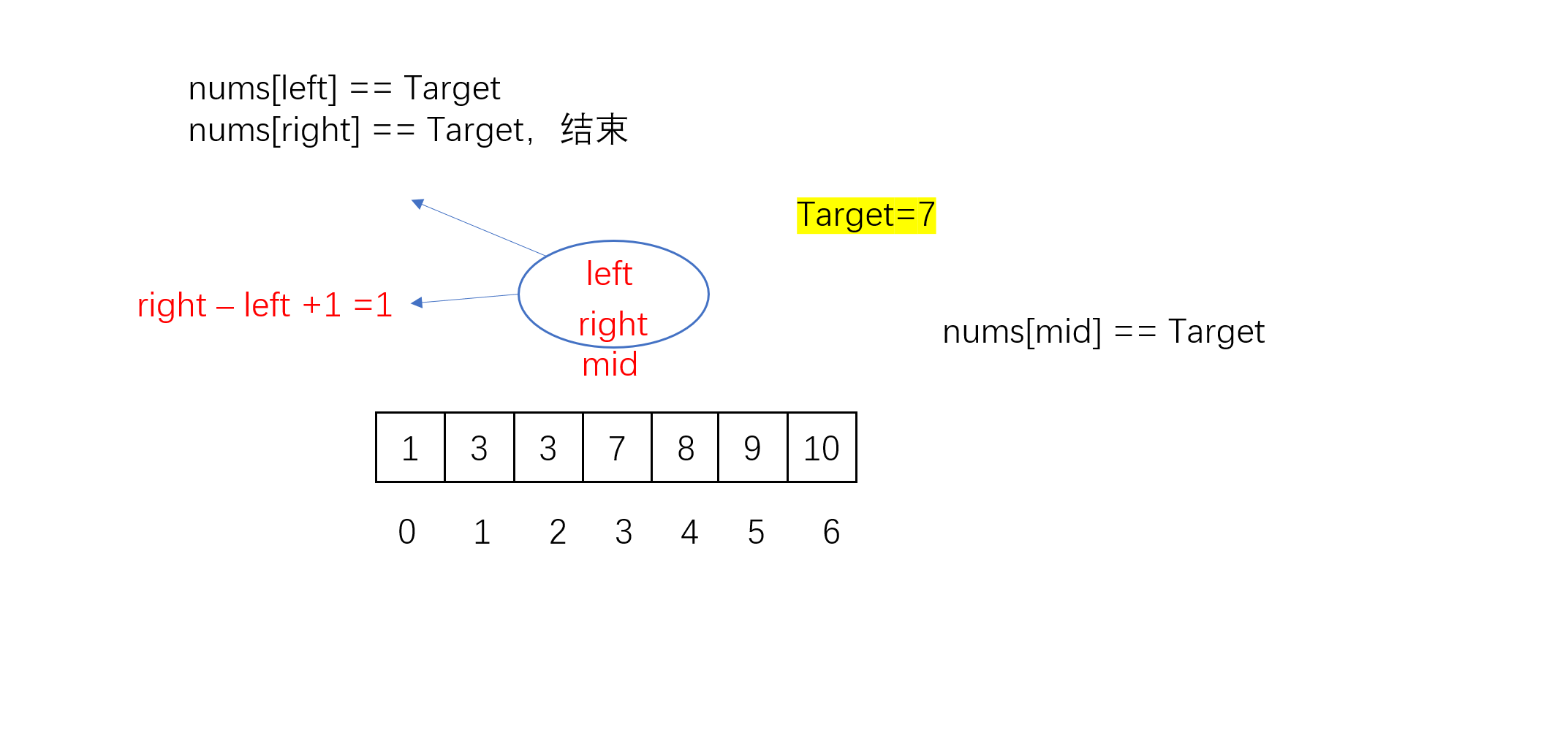
- 边界缩小:求出中间下标mid,如果nums[mid] > target,说明右边界在mid左边,因此缩小右边界right到mid-1;如果nums[mid] < target,说明左边界在mid右边,因此缩小左边界left到mid+1;而如果nums[mid] == target,我们显然不能将左右边界缩小到mid,这会导致跨过边界,只能一步步进行移动,即如果左边界不为目标值则left++,右边界不为目标值则right--;循环直到左右边界的值都为目标值,此时的left和right即为所找的边界。
- 返回区间个数:由于我们的边界是闭区间,所以区间内的元素个数为right-left+1,即为最终答案。
但笔者不太推荐这种方法,原因是这种方法在一些情况下时间复杂度会退化到O(N)。例如:
我们发现每次mid的值都为3,nums[mid]恒等于Targer ,left和right只能移动1步,最后相当于把数组遍历了一遍,时间复杂度退化为O(N)。
时间复杂度:采用二分法,时间复杂度O(logn);但在一些特殊情况如目标值正好在数组正中间时会退化为O(N)。
空间复杂度:只使用到了常数级的变量,空间复杂度为O(1)。
c.AC代码
//法1:循环计数,时间复杂度O(N),极度不推荐,代码略
//法2:两次二分法,时间复杂度O(logN),空间复杂度O(1)
int search(int* nums, int numsSize, int target)
{
int left = 0;
int right = numsSize - 1;
//找左边界
while (left <= right)
{
int mid = left + (right - left) / 2; //求中间值
if (nums[mid] >= target)
{
right = mid - 1;
}
else if (nums[mid] < target)
{
left = mid + 1;
}
}
int left_ans = left; //将左边界的下标保存起来
//检查左边界合法性,可选
if (left_ans >= numsSize || left_ans < 0 || nums[left_ans] != target)
{
return 0;
}
//重置用于找右边界
left = 0;
right = numsSize - 1;
while (left <= right)
{
int mid = left + (right - left) / 2;
if (nums[mid] > target)
{
right = mid - 1;
}
else if (nums[mid] <= target)
{
left = mid + 1;
}
}
int right_ans = right; //保存右边界
return right_ans - left_ans + 1; //闭区间,记得+1
}
//法3,一次二分找两边界,时间复杂度O(logN),但遇到特殊情况时间复杂度会退化到O(N),故不太推荐.空间复杂度O(1)
int search(int* nums, int numsSize, int target)
{
int left = 0;
int right = numsSize - 1;
while (left <= right)
{
int mid = left + (right - left) / 2; //求中间值
if (nums[mid] > target) //缩小右边界
{
right = mid - 1;
}
else if (nums[mid] < target) //缩小左边界
{
left = mid + 1;
}
else //等于目标值
{
if (nums[left] == target && nums[right] == target) //已经缩小到正确位置,break
break;
if (nums[left] != target) //一步步缩小
left++;
if (nums[right] != target)
right--;
}
}
return right - left + 1; //闭区间,记得+1
}四.0~n-1中缺失的数字
a.题目
b.题解分析
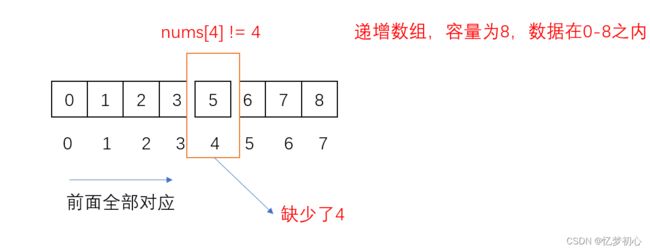
法1. 直接遍历
由于数组是递增数组,假如没有缺失数字,则每个位置的数字应该会下标构成一一映射的关系,即nums[0]=0,nums[1]=1......。因此我们只要遍历一次数组,当出现nums[i] != i时,则说明下标i位置对应的数缺失,返回缺失的数i。如果数组遍历完还没找到,则说明0-numsSize-1的数都存在,消失的数就为numsSize。
时间复杂度:遍历数组,时间复杂度O(N)。
空间复杂度:只使用到了常数级的变量,空间复杂度为O(1)。
法2. 位运算
根据异或运算x⊕x=0 和 x⊕0=x的运算规则,我们可以先将0~n-1的每个数进行异或,然后再将结果和数组nums中的每个元素进行异或,最后剩下的一定就是消失的数字。
时间复杂度:遍历数组进行异或运算,时间复杂度O(N)。
空间复杂度:只使用到了常数级的变量,空间复杂度为O(1)。
法3. 数学
除了用异或,我们也可以先将0~n-1的每个数进行相加,这里可以使用等差数列前n项和公式。然后再将结果和数组中每个元素进行相减抵消,剩下的就是消失的数字。
时间复杂度:遍历数组进行相减,时间复杂度O(N)。
空间复杂度:只使用到了常数级的变量,空间复杂度为O(1)。
法4. 二分查找
既然是递增数组,又让我们查找,那可不可以使用二分的方式呢?答案是可以的。我们只要找到第一次出现nums[i] != i的位置即可,二分的具体思路如下:
- 初始化:初始化左边界为0,右边界为numsSize-1。即闭区间。
- 锁定位置:先求出中间下标mid,如果nums[mid] == mid,则说明左半部分(包括mid)全部对应,消失的数字在右半部分,缩小左边界left到mid+1;如果nums[mid] != mid,则说明消失的数字在左半部分(包括mid),我们缩小右边界right到mid-1(当然这可能错过,但不影响)。循环直到left > right时我们就结束循环,此时的left即为消失的数字。
- 关于错过:可能有的人会有疑问,如果mid恰好是消失的数字,那right缩小到mid-1不就错过mid了吗?确实是错过了,但又没有真正错过
 。我们发现错过之后的nums[mid] 始终等于 mid,即left会一直往右走,right就不会动了,当left > right时left恰巧就是我们错过的位置,这也是为什么要返回left的原因。
。我们发现错过之后的nums[mid] 始终等于 mid,即left会一直往右走,right就不会动了,当left > right时left恰巧就是我们错过的位置,这也是为什么要返回left的原因。
时间复杂度:采用二分法,时间复杂度O(logn)。
空间复杂度:只使用到了常数级的变量,空间复杂度为O(1)。
c.AC代码
//法1,排序数组直接遍历查找 时间O(N),空间O(1)
int missingNumber(int* nums, int numsSize)
{
//数组下标0-numsSize-1 , 数据范围0 - numsSize
int k = 0;
for (k = 0; k < numsSize; k++)
{
if (nums[k] != k)//不为k说明k为消失的数字
{
return k;
}
}
//0-numsSize-1都存在,则k==numsSize即为消失的数字
return k;
}
//法2,异或 时间O(N),空间O(1)
int missingNumber(int* nums, int numsSize)
{
int val = 0;
//对0-numsSize的数字进行异或
for (int i = 0; i <= numsSize; i++)
{
val ^= i;
}
//再对数组每个元素进行异或
for (int i = 0; i < numsSize; i++)
{
val ^= nums[i];
}
return val;
}
//法3,0-(n-1)全部相加然后与数组相减 时间O(N),空间O(1)
int missingNumber(int* nums, int numsSize)
{
int sum = 0;
//对0-numsSize的数字进行相加
for (int i = 0; i <= numsSize; i++)
{
sum += i;
}
//再减去数组的每个元素
for (int i = 0; i < numsSize; i++)
{
sum -= nums[i];
}
return sum;
}
//法4,采用二分法 时间O(logN),空间O(1)
int missingNumber(int* nums, int numsSize)
{
int left = 0;
int right = numsSize - 1;
while (left <= right)
{
int mid = left + (right - left) / 2;
if (nums[mid] == mid) //left右移
{
left = mid + 1;
}
else //nums[mid] != mid ,right左移
{
right = mid - 1;
}
}
return left;
}
以上,就是本期的全部内容啦
制作不易,能否点个赞再走呢