Network Dissection 论文阅读笔记
Network Dissection 论文阅读笔记
- 1. 简介
- 2. 网络刨析
-
- 2.1 深度视觉表征的可解释性的测量步骤
- 2.2 数据集
- 2.3 可解释神经元评分
- 3. 实验
-
- 3.1 对解释的人类评价
- 3.2 Measurement of Axis-Aligned Interpretability
- 3.3 理解层概念
- 3.4 网络架构和监督
- 3.5 训练条件 vs 可解释性
- 3.6 网络的分类能力 vs 可解释性
- 3.7 层宽度 vs 可解释性
- 4. 问答
- 参考
1. 简介
这是CVPR2017一篇有关深度学习可解释性研究的文章,作者通过评估单个隐藏神经元(unit)与一系列语义概念(concept)间的对应关系,来量化 CNN 隐藏表征的可解释性。
2. 网络刨析
2.1 深度视觉表征的可解释性的测量步骤
- 确定一套广泛的人类标记的视觉概念集合。
- 收集隐藏神经元对已知概念的响应。
- 量化(隐藏神经元,概念)的映射方式。
2.2 数据集
作者建立了一个完善的测试数据集,叫做Broden(Broadly and Densely Labeled Dataset),每张图片都在场景、物体、材质、纹理、颜色等层面有pixel-wise的标定。Broden 数据集中的样本示例如下图所示。

2.3 可解释神经元评分
将该数据集中的每一张图喂给需要分析的网络,拿到每个feature map 上的响应结果,进一步分析该层feature map对应的语义关系,归纳结果。整体流程如下图所示。
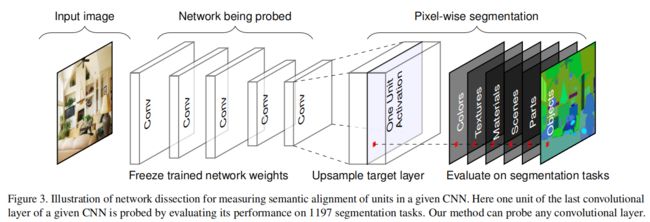
对于Broden数据集中的每个输入图像 x x x,收集每个内部卷积核 k k k 的激活映射 A k ( x ) A_k (x) Ak(x)。然后计算了单个卷积单元激活量的分布情况 a k a_k ak。对于每个单元 k k k ,在数据集中的激活映射的每个空间位置上,通过 P ( a k > T k ) = 0.005 P(a_k>T_k)=0.005 P(ak>Tk)=0.005 确定上分位数 T k T_k Tk。
为了比较低分辨率单元的激活映射与输入分辨率注释掩码 L c L_c Lc 的某些概念 c c c,使用双线性插值将激活特征图 A k ( x ) A_k(x) Ak(x) 放大到输入掩码分辨率 S k ( x ) S_k(x) Sk(x),将插值固定在每个单元的接受域的中心。
然后将 S k ( x ) S_k(x) Sk(x) 按阈值进行一个二进值分割: M k ( x ) ≡ S k ( x ) ≥ T k M_k(x)≡S_k(x)≥T_k Mk(x)≡Sk(x)≥Tk,选择激活特征图超过阈值 T k T_k Tk 的所有区域。通过对每对 ( k , c ) (k,c) (k,c) 计算交集 M k ( x ) ∩ L c ( x ) M_k(x)∩L_c(x) Mk(x)∩Lc(x),对数据集中的每个概念 c c c 进行评估。
每个单元 k k k 作为概念 c c c 的分割得分通过以下交并比公式计算:
I o U k , c = ∑ ∣ M k ( x ) ∩ L c ( x ) ∣ ∑ ∣ M k ( x ) ∪ L c ( x ) ∣ IoU_{k,c} = \frac{\sum|M_k(x) ∩ L_c(x)|}{\sum|M_k(x) ∪ L_c(x)|} IoUk,c=∑∣Mk(x)∪Lc(x)∣∑∣Mk(x)∩Lc(x)∣
这里 ∣ ⋅ ∣ |\cdot| ∣⋅∣ 是一个集合的基数。因为数据集包含一些类型的标签,这些标签不存在在某些输入子集上,仅仅在图像子集上至少有一个与 c c c 相同的概念标签时计算求和。 I o U k , c IoU_{k,c} IoUk,c 的值是单元 k k k 检测概念 c c c 的精度;如果 I o U k , c IoU_{k,c} IoUk,c 超过一个阈值(文中设置为0.04),我们考虑一个单元 k k k 作为概念 c c c 的检测器。请注意,一个单元可能是多个概念的检测器(一个概念也可能被多个单元检测到);为了进行分析,我们选择了排名靠前的标签。为了量化一个层的可解释性,我们计算检测唯一概念单元的数量,称之为唯一探测器的数量 (number of unique detectors)。
3. 实验
3.1 对解释的人类评价
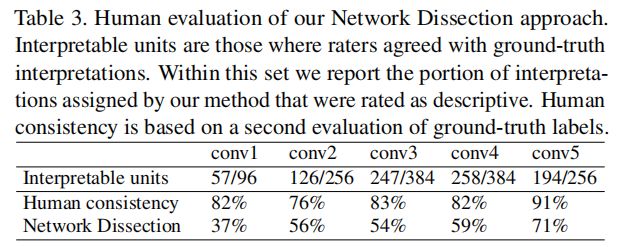
在最底层,Broden中可用的低级颜色和纹理概念仅足以匹配少数单元的良好解释。人类的一致性在conv5中也最高,这表明人类更善于识别和同意高级的视觉概念,如物体和部分,而不是出现在较下层的形状和纹理。
3.2 Measurement of Axis-Aligned Interpretability
为了探究网络的可解释性(Interpretability)是否与单元(units)的排列分布有关,作者对于某一层的所有单元进行random linear combination(下图Q),也即打乱该排布方式,而后将打乱的次序归位(下图 Q − 1 Q^{-1} Q−1),观察concept的变化情况得到结果。具体如下图所示:
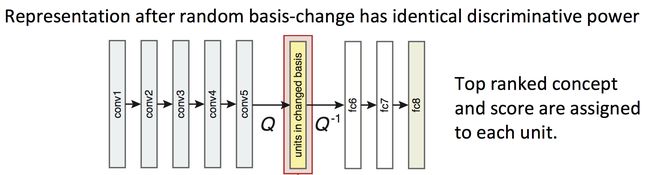
其中,rotation的大小代表了random Q的程度大小,而打乱这些units的排布并不会对于网络的最终输出产生影响,同时也不会改变该网络的表达能力(discriminative power)。
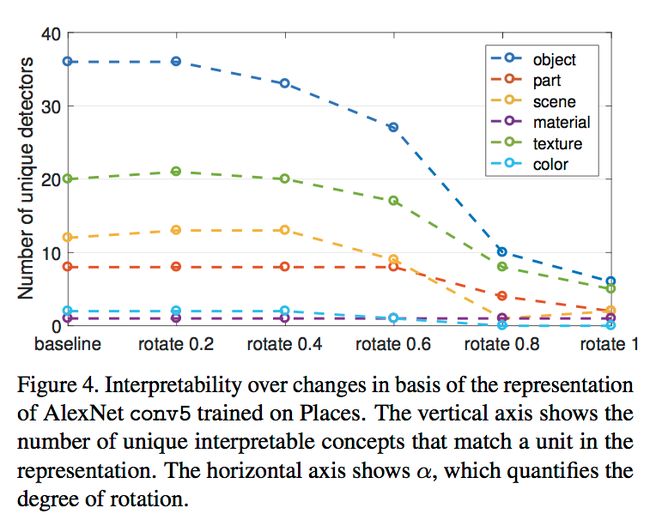
可以从结果中发现,随着rotation的逐渐变大,number of unique detectors开始急剧减少,因此CNN网络的可解释性是受到unit的排序的影响的。
3.3 理解层概念
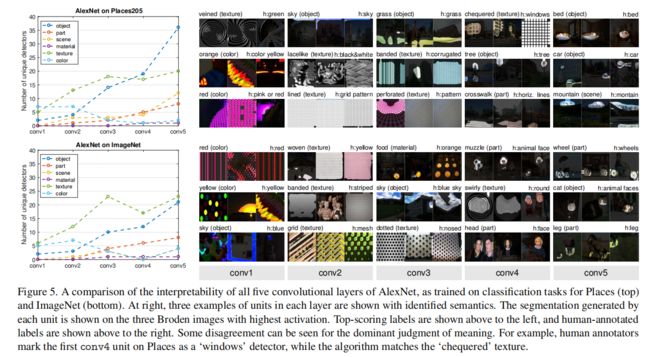
证实直觉,color和texture概念在较低的conv1和conv2占主导地位,而conv5出现了更多的object和part探测器。
3.4 网络架构和监督
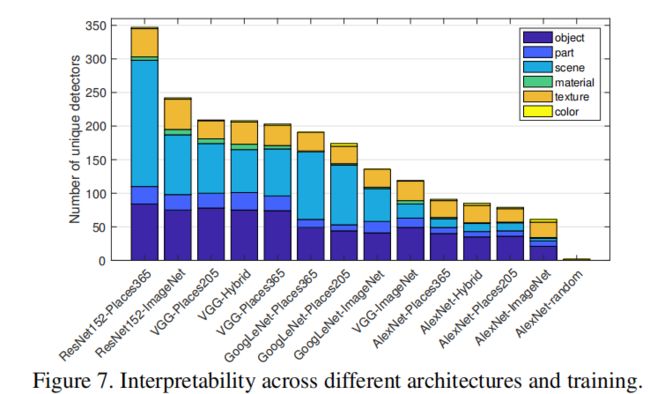
在网络架构方面,我们发现可解释性ResNet > VGG > GoogLeNet > AlexNet。更深层次的架构似乎允许更大的可解释性。
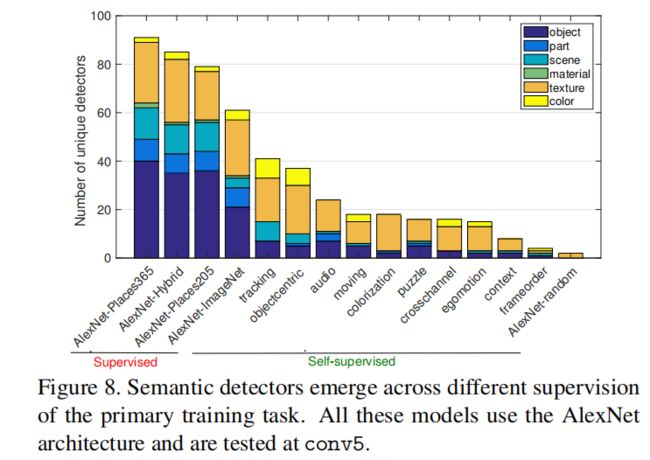
自监督模型创建了许多纹理检测器,但相对较少的对象检测器;显然,在大型注释数据集上,自监督学习任务可解释性要比监督学习任务弱得多。
3.5 训练条件 vs 可解释性
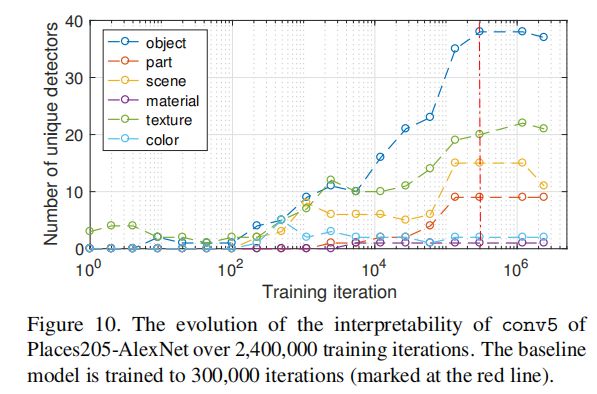
上图绘制了不同训练迭代下基线模型快照的可解释性。我们可以看到,object检测器和part检测器在大约10,000次迭代中开始出现(每次迭代处理256幅图像)。我们在训练期间我们没有发现不同概念类别之间转换的证据。例如,conv5中的单元在成为object或part检测器之前不会变成texture或material检测器。
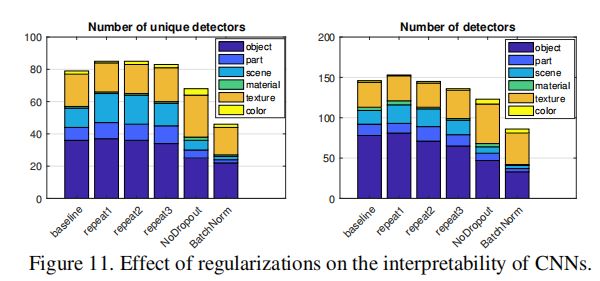
上图中repeat1,repeat2,repeat3代表三种不同的权重初始化方式,结果表示:
- 比较不同的随机初始化,模型在唯一检测器数和总检测器数方面都收敛于相似的可解释性水平;
- 对于没有Dropout的网络,出现的texture检测器更多,但出现的object检测器更少;
- 批处理规范化似乎显著降低了可解释性。
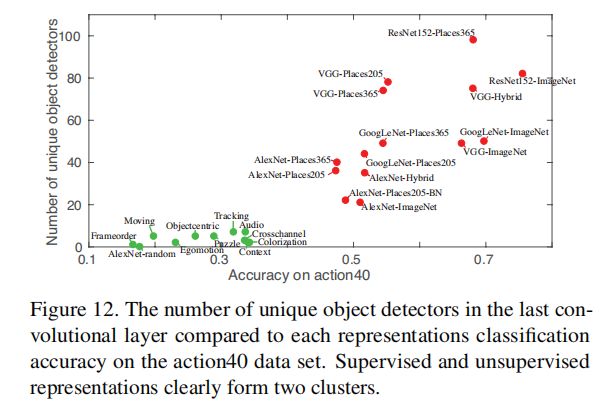
3.6 网络的分类能力 vs 可解释性
3.7 层宽度 vs 可解释性
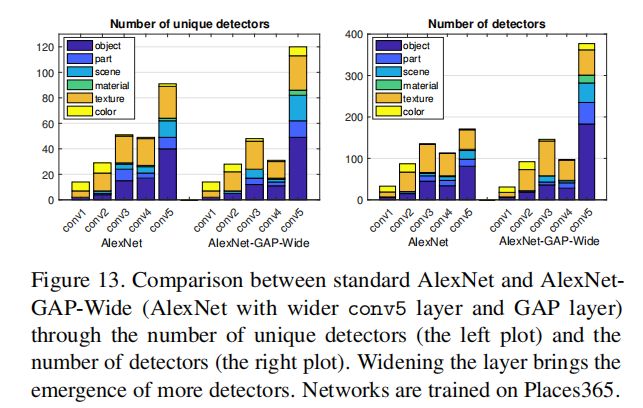
conv5的卷积核从256增加到768,在验证集上具有与标准AlexNet相似的分类精度,但是在conv5上出现了很多独立检测器和检测器;我们还将conv5的单元数量增加到1024和2048,但独立概念的数量没有进一步显著增加。这可能表明AlexNet分离解释因素的能力有限;或者它可能表明限制解开概念的数量有助于解决场景分类的主要任务。
4. 问答
在以下参考内容[2]、[3]、[4]中记录了一些作者本人回答的问题,可以帮助更好理解文章。
参考
[1] Network Dissection:
Quantifying Interpretability of Deep Visual Representations
[2] 论文笔记:《Network Dissection: Quantifying Interpretability of Deep Visual Representations》–CSDN
[3] 从深度神经网络本质的视角解释其黑盒特性–知乎
[4] 知乎大神周博磊:用“Network Dissection”分析卷积神经网络的可解释性