dp算法篇Day11
“哎呀,哎呀,流云开一朵,哟诶嘿哟,哟诶嘿哟~”
51、目标和
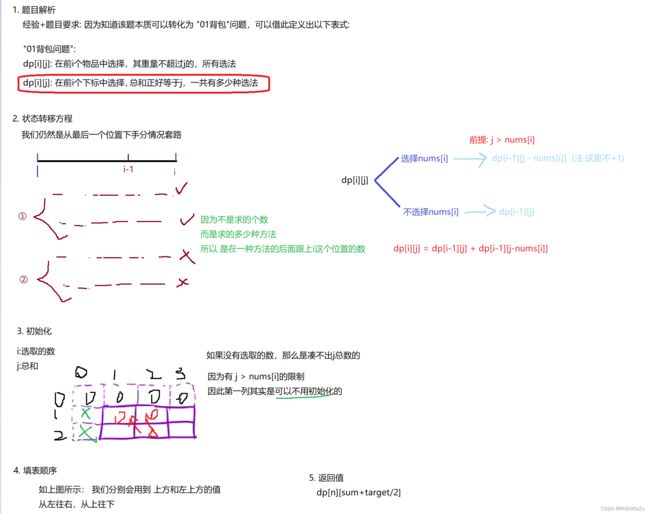
(1) 题目解析
包括之后的一些题目,乍一眼看可能你不会发现它与dp问题有何相连,可是按照按照题目又难以想出 思路、写出代码来。因此,解决这一类问题的关键,现在倒不是状态表示或状态转移方程,而是如何将题目的思路进行转化。
(2) 算法原理
class Solution {
public:
int findTargetSumWays(vector& nums, int target) {
int sum = 0;
for(auto& e:nums) sum += e;
int aim = (sum + target) / 2;
// 处理边界
// aim是所有正数的和 sum + target只有是偶数时才能分两个
if(aim < 0 || (sum + target) % 2) return 0;
int n = nums.size();
vector> dp(n+1,vector(aim+1));
dp[0][0] = 1;
for(int i=1;i<=n;++i)
// 注:这里因为第一列没有必要做初始化 所以从0开始
for(int j=0;j<=aim;++j)
{
dp[i][j] = dp[i-1][j];
if(j >= nums[i-1]) dp[i][j] += dp[i-1][j-nums[i-1]];
}
return dp[n][aim];
}
}; 优化:
class Solution {
public:
int findTargetSumWays(vector& nums, int target) {
int sum = 0;
for(auto& e:nums) sum += e;
int aim = (sum + target) / 2;
// 处理边界
// aim是所有正数的和 sum + target只有是偶数时才能分两个
if(aim < 0 || (sum + target) % 2) return 0;
int n = nums.size();
vector dp(aim+1);
dp[0] = 1;
for(int i=1;i<=n;++i)
for(int j=aim;j >= nums[i-1];--j)
{
if(j >= nums[i-1]) dp[j] += dp[j-nums[i-1]];
}
return dp[aim];
}
}; 52、最后一块石头的重量
(1) 题目解析 
读完题目,以及即便看懂了题目举的例子,恐怕你的脑子里也很难立马生成如何解决这个问题的思路。这同样是一道类似"背包问题"的题目,关键就在于如何讲题目信息,求解内容进行转化。
(2) 算法原理 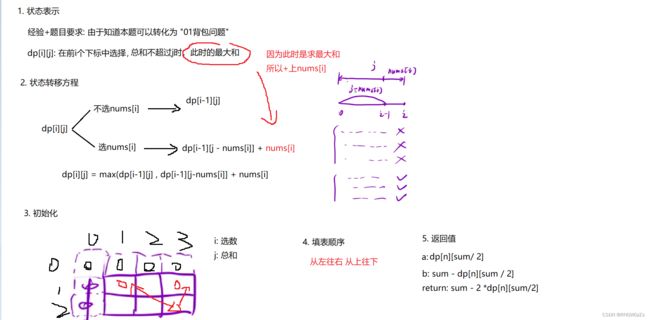
class Solution {
public:
int lastStoneWeightII(vector& stones) {
int sum = 0;
for(auto& e:stones) sum += e;
int aim = sum / 2;
int n =stones.size();
vector> dp(n+1,vector(aim+1));
for(int i=1;i<=n;++i)
for(int j=0;j<=aim;++j)
{
dp[i][j] = dp[i-1][j];
if(j >= stones[i-1]) dp[i][j] = max(dp[i][j],dp[i-1][j-stones[i-1]] + stones[i-1]);
}
return sum - (dp[n][aim])*2;
}
}; 优化:
class Solution {
public:
int lastStoneWeightII(vector& stones) {
int sum = 0;
for(auto& e:stones) sum += e;
int aim = sum / 2;
int n =stones.size();
vector dp(aim+1);
for(int i=1;i<=n;++i)
for(int j=aim;j >= stones[i-1];--j)
{
dp[j] = max(dp[j],dp[j-stones[i-1]] + stones[i-1]);
}
return sum - (dp[aim])*2;
}
}; 53、完全背包
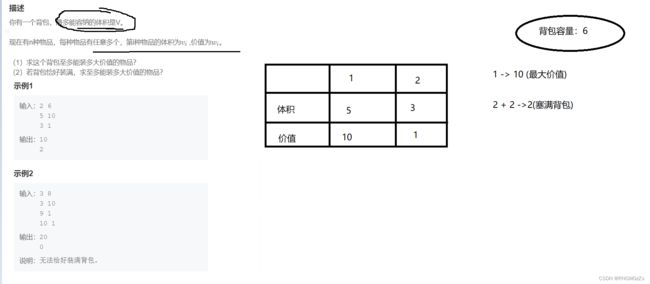
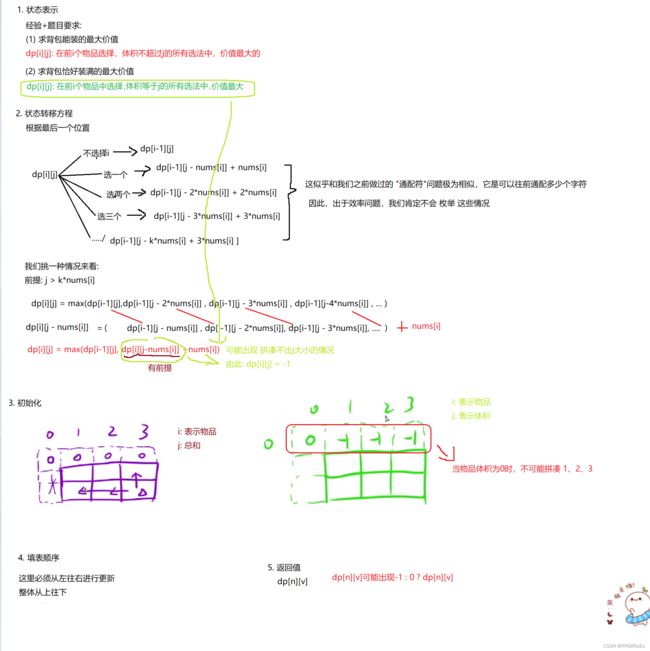
(1) 题目解析
在之前介绍背包问题时,也谈到过完全背包是怎么回事,其实就是一个物品的数量可以有多个,也就是可以被选择多次。这同拿到背包问题一样,是一道模板题型。其中的分析思路,可以适用很多可以转化为背包场景的问题中。
(2) 算法原理
#include
#include
#include
using namespace std;
const int N = 1024;
int dp[N][N];
// 体积+价值
int V[N],W[N];
int n,v;
int main()
{
cin >> n >> v;
// 录入数据
for(int i=1;i<=n;++i)
cin >> V[i] >> W[i];
for(int j=0;j<=v;++j) dp[0][j] = 0;
for(int i=1;i<=n;++i)
for(int j=0;j<=v;++j)
{
dp[i][j] = dp[i-1][j];
if(j >= V[i]) dp[i][j] = max(dp[i][j],dp[i][j-V[i]] + W[i]);
}
cout << dp[n][v] << endl;
memset(dp,0,sizeof(dp));
// 初始化
for(int j=1;j<=v;++j) dp[0][j] = -1;
for(int i=1;i<=n;++i)
for(int j=0;j<=v;++j)
{
dp[i][j] = dp[i-1][j];
// 边界
if(j >= V[i] && dp[i][j-V[i]] != -1)
dp[i][j] = max(dp[i][j],dp[i][j-V[i]] + W[i]);
}
cout << (dp[n][v] == -1 ? 0 : dp[n][v]) << endl;
}
优化:
#include
#include
#include
using namespace std;
const int N = 1024;
// 体积+价值
int V[N],W[N];
int n,v;
int main()
{
cin >> n >> v;
// 录入数据
for(int i=1;i<=n;++i)
cin >> V[i] >> W[i];
int dp[v];
for(int j=0;j<=v;++j) dp[j] = 0;
for(int i=1;i<=n;++i)
for(int j=V[i];j<=v;++j) // 从左到右
{
dp[j] = max(dp[j],dp[j-V[i]] + W[i]);
}
cout << dp[v] << endl;
memset(dp,0,sizeof(dp));
// 初始化
for(int j=1;j<=v;++j) dp[j] = -0x3f3f3f3f;
for(int i=1;i<=n;++i)
for(int j=V[i];j<=v;++j)
{
// 边界dp[j-V[i]] + W[i]当不存在是 是一个很小的数
dp[j] = max(dp[j],dp[j-V[i]] + W[i]);
}
cout << (dp[v] < 0 ? 0 : dp[v]) << endl;
} 54、零钱兑换
(1) 题目解析
其实很多时候,遇到这种选与不选的题型,你就应该往背包问题上思考。
(2) 算法原理
class Solution {
public:
int coinChange(vector& coins, int amount) {
int n = coins.size();
int INT_INFO = 0x3f3f3f3f;
// 初始化
vector dp(amount+1,INT_INFO);
dp[0] = 0;
for(int i=1;i<=n;++i)
for(int j=coins[i-1];j<=amount;++j)
dp[j] = min(dp[j],dp[j-coins[i-1]] + 1);
return dp[amount] >= INT_INFO ? -1 : dp[amount];
}
};
55、零钱兑换Ⅱ
(1) 题目解析
从题目看,也知道这道题肯定和上一道题有着密切的关系。是的!这道题也是一道可以被转换成"完全背包"的题型。相反,上一道题是求的能填满背包的最少物品,这次是求的是填满背包有多少种方法。
(2) 算法原理
class Solution {
public:
int change(int amount, vector& coins) {
int n = coins.size();
vector dp(amount+1);
dp[0] = 1;
for(int i=1;i<=n;++i)
for(int j=coins[i-1];j<=amount;++j) // 从左往右
{
dp[j] += dp[j-coins[i-1]];
}
return dp[amount];
}
}; 本篇到此结束,感谢你的阅读。
祝你好运,向阳而生~