科学计算库—numpy随笔【五一创作】
文章目录
-
- 8.1、numpy
-
- 8.1.1、为什么用 numpy?
- 8.1.2、numpy 数据类型推理
- 8.1.3、numpy 指定长度数组快速创建
- 8.1.4、numpy 哪个是行、列?
- 8.1.5、numpy 如何进行数据类型转换?
- 8.1.6、numpy 有几种乘法?
- 8.1.7、numpy 索引和切片操作
-
-
- 8.1.8、numpy 比较运算
- 8.1.9、numpy 如何指定行列?
- 8.1.10、numpy 如何转置?
- 8.1.11、numpy where 函数
- 8.1.12、 numpy 如何值替换?
- 8.1.13、numpy 数学运算
8.1、numpy
本质是多维数组对象
list 类型转为 numpy 数组 更有利科学计算
8.1.1、为什么用 numpy?
1.虽然Python数组结构中的列表list实际上就是数组,但是列表list保存的是对象的指针,list中的元素在系统内存中是分散存储的,例如[0,1,2]需要3个指针和3个整数对象,浪费内存和计算时间。
2.NumPy数组存储在一个均匀连续的内存块中,访问更快;NumPy中的矩阵计算可以采用多线程的方式,计算更快。
结论:numpy 可提供高性能的矩阵运算,作为数组 numpy 提供了许多方便统计计算的功能,数组结构为ndarray。
numpy 和 list 有什么区别?
从存储数据来看,numpy 存储的是矩阵,list 存储的是序列
下面举个例子
li = [1,2,3,4]Out: [1, 2, 3, 4]
arr = np.array(li)Out: [1 2 3 4]
8.1.2、numpy 数据类型推理
numpy 会对数据类型进行推理,规则:转为适用性更强的数据类型。
下面举个例子:
为什么会进行数据类型推理?
numpy 适合处理统一的数值数组数据,数据类型推理就是为了保证数值类型统一。
8.1.3、numpy 指定长度数组快速创建
”零矩阵“
np.zeros()
np.zeros((3,4))
np.zeros((1,3,4))
np.zeros((1,1,3,4))
超出二维后的形式,以
np.zeros((1,3,4))为例,嵌套1层,层内3行4列;array([[[0., 0., 0., 0.], [0., 0., 0., 0.], [0., 0., 0., 0.]]])(1,1,3,4)相比(1,3,4),增加一维,多嵌套一层:
array([[[0., 0., 0., 0.], [0., 0., 0., 0.], [0., 0., 0., 0.]]])(2,1,3,4)相比(1,1,3,4),数值增加,平行矩阵增加:
array([[[[0., 0., 0., 0.], [0., 0., 0., 0.], [0., 0., 0., 0.]]], [[[0., 0., 0., 0.], [0., 0., 0., 0.], [0., 0., 0., 0.]]]])
补充:
”1矩阵“
np.ones((row,col))
8.1.4、numpy 哪个是行、列?
最后两组数为行和列。
倒是第一组为列,倒数第二组为行(若存在)
8.1.5、numpy 如何进行数据类型转换?
arr = np.array([1.1,1.2,-1,-3.3])
以 arr 为例,将 arr 内的数据类型转为 int32:
arr.astype(np.int32)
8.1.6、numpy 有几种乘法?
四种。
1)星乘(*)
数组的对应元素相乘
arr1 * arr2
2)点乘(np.dot)
就是矩阵乘法
a = np.array([...])
b = np.array([...])
np.dot(a,b)
3)叉乘(np.cross)、外乘(np.outer)
细说NumPy数组的四种乘法的使用
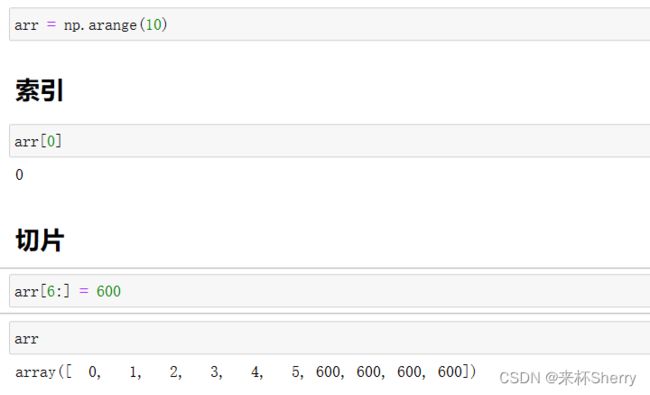
8.1.7、numpy 索引和切片操作
举个例子:
补充:
花式索引
通过整型数组进行索引
花式索引为什么有两层中括号?
以数组对象 arr 为例,向arr[]中传入数组作为参数,所以才有了两个中括号
在机器学习中常通过使用花式索引来打乱数据集的样本顺序,避免机器学习模型学习到样本的位置噪声,对于监督学习的数据集如果打乱了样本还需要打乱相对应的标签值,样本与标签都是一一对应的关系,使用花式索引能够轻松的解决。
注意,这里有一个问题:
arr = np.arange(12).reshape((3,4)) print(arr[[0,2]])Out:
[[ 0 1 2 3] [ 8 9 10 11]]换一个写法,将 reshape 拆开,无法得到想要的结果(尚不知具体原因):
arr.reshape() 本身不会改变arr,而是得到改变形状后的一个返回值,这就是原因。——2023.7.11
d = np.arange(12) print(d.reshape(3,4)[[0,2]])要用花式索引,不要让reshape方法‘’单着‘’
Out:
[[ 0 1 2 3] [ 8 9 10 11]]
8.1.8、numpy 比较运算
names = np.array(['名字1','名字2','名字3'])
sex = np.array(['M','F'])
这里举几个 and、or 的例子:
(names == '名字4') & (sex == 'M')Out:array([False, False, False])
(names == '名字1') | (names == '名字5')Out:array([ True, False, False])
8.1.9、numpy 如何指定行列?
arr = np.arange(16)
以 arr 为例,整成 4行4列:
arr.reshape(4,4)Out:
array([[ 0, 1, 2, 3], [ 4, 5, 6, 7], [ 8, 9, 10, 11], [12, 13, 14, 15]])
8.1.10、numpy 如何转置?
比 list 强大之处,举个例子:
arr = np.arange(24).reshape((3,8))arr.T#转置Out:
array([[ 0, 8, 16], [ 1, 9, 17], [ 2, 10, 18], [ 3, 11, 19], [ 4, 12, 20], [ 5, 13, 21], [ 6, 14, 22], [ 7, 15, 23]])
补充:
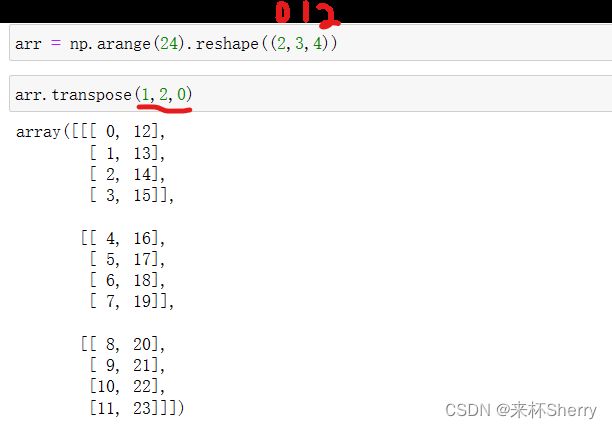
轴转置
arr 为三维矩阵,初始时刻存在的三个轴下标分别0、1、2,基于下标完成轴转置,如下图:
8.1.11、numpy where 函数
res = [x if c else y for x,y,c in zip(x_arr,y_arr,conditon)]#list对象
res = np.array(res)#numpy对象
等价表示
res = np.where(condition,x_arr,y_arr) #返回numpy对象
若条件 condition 成立,取 x_arr,否则取 y_arr 。
8.1.12、 numpy 如何值替换?
arr = np.random.randn(4,4)# 4*4随机矩阵
利用8.1.11提到的where函数,实现值替换,举个例子,将正数替换为5,负数为-5:
arr = np.where(arr>0,5,-5)
8.1.13、numpy 数学运算
1)生成随机矩阵
例如生成一个4*4随机矩阵:
arr = np.random.randn(4,4)
随机矩阵生成,数据源有两种,
np.random.rand()
np.random.randn()
rand() :取值从0,1之间的均匀分布中抽样。
randn():取值从以0为均值,1为方差的标准正态分布中抽样。
例如,生成4 * 4 随机矩阵,
arr = np.random.randn(4,4)# 4*4随机矩阵 print(arr) arr = np.random.rand(4,4)# 4*4随机矩阵 print(arr)Out:
[[-0.38672283 0.2510875 0.84164035 -1.171516 ] [-0.34456511 -1.43556016 0.78061698 0.68466033] [-1.05684828 0.66353918 -0.16626838 -1.0837476 ] [-0.54743772 -0.70599557 -0.24332244 -0.18156644]] [[0.63981419 0.56708754 0.03062314 0.77049354] [0.79681395 0.12707638 0.05749961 0.21459898] [0.62925634 0.10423857 0.47172718 0.57837616] [0.68260032 0.54003265 0.57571165 0.50320049]]
2)平均值、求和
怎么确定 axis 方向?
以 arr 对象为例:
arr.mean()#对所有元素
arr.mean(axis = 0)#0轴沿着行的方向垂直向下运算
arr.mean(axis = 1)#1轴沿着列的方向水平延伸运算
arr.sum()
3)排序
以 arr 对象为例:
arr.sort():返回的是原数组的“视图”,而不是 copy
np.sort(arr):返回的是原数组的 copy, 而不是“视图”,当有保留原 arr 需求时用这个