笔记(总结)-卷积神经网络
神经网络是一棵根深叶茂的大树,有过许多果实,可是都略显青涩,无法摘食。直到2010年后,这棵大树才真正可谓硕果累累,其中最璀璨甘甜的就是卷积神经网络(Convolutional Neural Network,下称CNN)。在这之后,神经网络再次成为科研界的热点,在这个数据和算力初具规模的时代,神经网络终于展现出了应用的价值。闲话到此,只是想说明CNN对于神经网络的意义。本篇将主要讨论CNN的模型原理,并简述其在分类问题上的应用。
起源
全连接前馈神经网络(前馈神经网络指一层神经元只接受上一层作为输入,并输出到下一层,该层神经元之间、该层与其它层都没有连接关系)以其复杂的连接方式,在一段时间内展现出了很强的拟合能力。但是面对特定问题时,展示出了缺陷。比如面对图像问题时,各像素点打平变成一个向量输入时,假设图像尺寸为10*10=100个像素点,隐层神经元有1024个,那么参数个数为100*1024个,如此大的参数空间,在训练时是无法忍受的。
CNN也是一种前馈神经网络,受生物学上的“感受野”机制带来的灵感而提出。
感受野主要是指听觉系统、本体感觉系统和视觉系统中神经元的一些性质。比如在视觉神经系统中,一个神经元的感受野是指视网膜上的特定区域,只有这个区域内的刺激才能够激活该神经元。
CNN具有感受野提取特征的能力,参数少、训练快等诸多优点。很好地解决了图像特征提取的问题。
接下来的叙述思路为理解CNN,即在给定CNN的结构下,如何理解CNN中各部分的设计与功能。由于能力有限,如果按照“如何得出CNN的结构设计”这一种方式来讲,恐怕难以讲清,虽然这种思路是更加自然的,也是CNN发明者的智慧精华所在。
整体设计
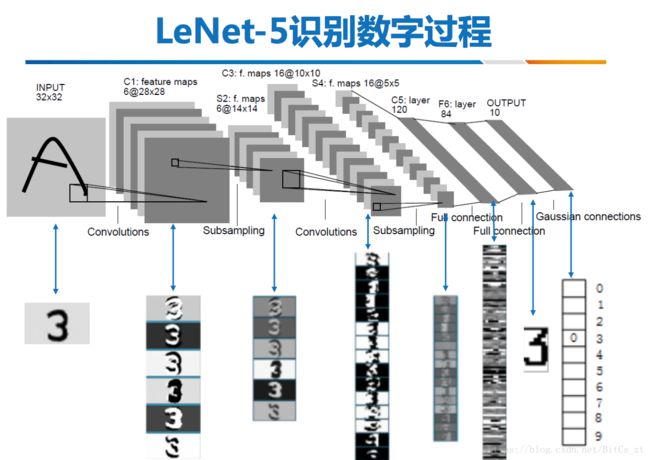
以图像分类问题为例(即给定一副图,根据图片内容,将图片分类到相关类别),CNN架构图如下:

原始图片的像素作为原始特征输入到神经网络中,经过卷积层(Convolution)-池化层(Pooling)组合模块的堆叠,完成特征提取过程,此时得到的是图像的高维特征表示。然后将特征打平(Flatten),输入到全连接网络中,完成分类功能。可以看到,整个CNN的架构、功能分为清晰的两部分:卷积-池化模块的特征抽取+全连接网络的分类。其中全连接网络是已经知道的,CNN的贡献在于前一部分。
题外话:单独的前馈神经网络其实也可以看做两个模块,中间隐层完成了特征提取过程,最后一层完成了分类过程。但由于网络层都是全连接,特征提取和分类某种程度上杂糅了起来,耦合度比较高。这样的网络在训练时其实是不好做的。而CNN很好的解决了这个问题,架构上进行了解耦,模块各司其职,优化也可以分别进行。
卷积层(Convolution Layer)
考虑一张简单的6*6的像素图,像素不含灰度值时(像素点取值为0或1),表示如下图。
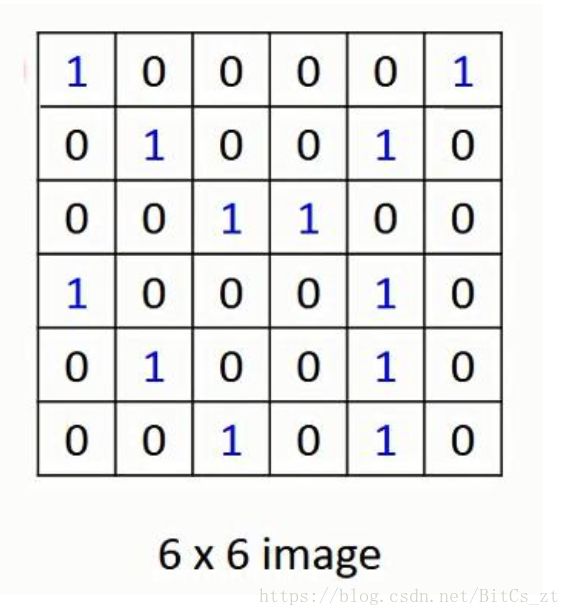
卷积层主要由卷积核(filter)构成。逻辑上来说,卷积核是形如下图的参数矩阵:
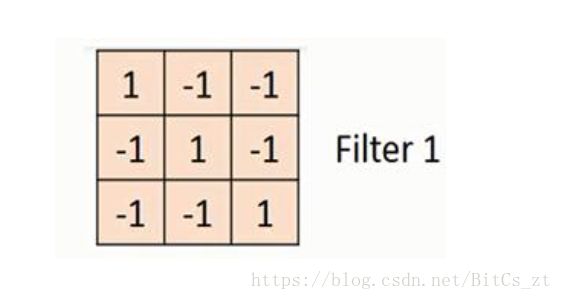
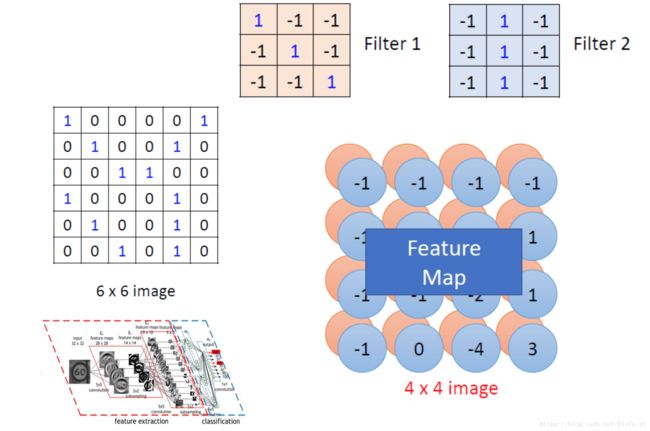
卷积核与像素矩阵进行卷积运算,得到特征,卷积神经网络也因此得名。运算图如下:
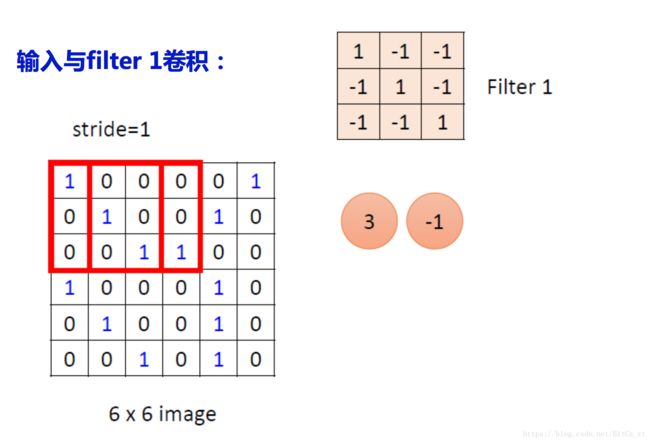
可以看到,卷积核与像素矩阵中同尺寸的部分进行点积运算(即两个同尺寸矩阵的对应元素相乘,对乘积结果进行求和),公式化表示如下:
卷积核和像素矩阵的不同部分做卷积运算,提取出不同的 feature f e a t u r e 。可以想象卷积核贴附在像素矩阵上方,沿着不同方向滑动(stride),从而提取不同区域的特征。最终得到特征矩阵,特征矩阵的尺寸与卷积核尺寸、滑动步长、像素矩阵相关。
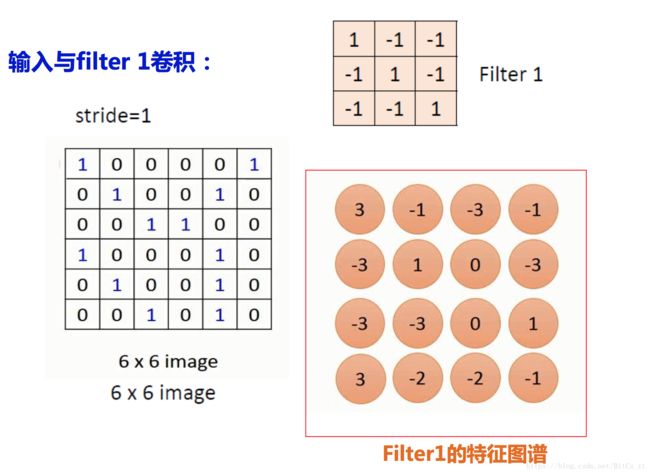
当使用多个卷积核时,便能得到多个特征矩阵。对于卷积核,我们可以理解为特征提取器,这种特征可能是图像中的轮廓、边角、颜色等信息。卷积核1提取整个图像上的轮廓信息,卷积核2提取整个图像上的颜色信息等等。而特征矩阵则是整个图像矩阵不同局部的某种特征表示。
直观上来看,卷积核只是完成了卷积运算,而提取出的特征也不过是乘积求和的数值。但由于神经网络有惊人的拟合能力,BP优化的过程中能产生很多神奇的效果。当我们拿到卷积层的中间结果,并进行合理展示时,这种特征提取过程更加明显(数学确实是个神奇的东西,这种结果看起来不可思议):
以上分析都是基于卷积层的逻辑视图。考虑卷积层计算的物理视图(转化为神经网络的神经元计算)。像素矩阵按行列打平,作为输入神经元;特征矩阵中的元素相当于隐层神经元;而卷积核则相当于权值参数。卷积运算的过程实际上就是:输入神经元的特定部分,乘以权值矩阵,得到隐层神经元的过程。
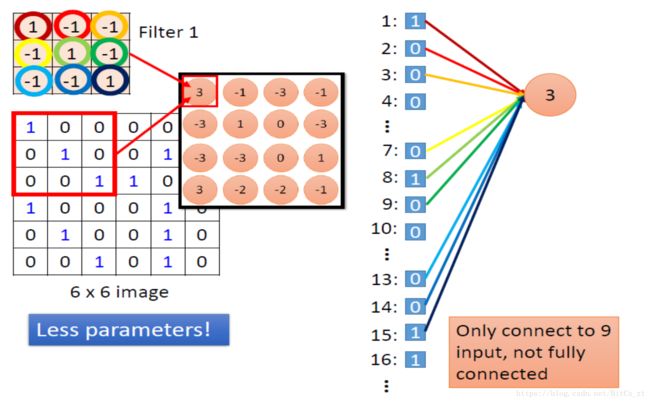
由上图可以看到,相比于全连接神经网络,每个隐层神经元和每个输入神经元都有连接。卷积层只是进行了局部连接(稀疏连接)。

除此之外,卷积层还进行了参数共享。由之前的逻辑视图已经看到,卷积核在提取每个局部特征的过程中,是不变的。结合上图可以看到,同一卷积核得到的不同隐层神经元,与输入神经元连接的参数是一样的。
这两者结合起来,极大地减少了卷积层的参数空间。并且由逻辑视图可以看到,卷积核在不同图像局部的卷积运算、不同的卷积核的卷积运算都是相互独立,可以使用并行计算来加速卷积层的运算。这也是CNN在工业界能够得到大规模应用的原因。
池化层(Pooling Layer)
卷积层在小参数空间下完成了特征提取,然而特征矩阵(隐层)神经元的个数仍然是众多的。当像素矩阵巨大时,特征矩阵的神经元个数就会变得很多(一般卷积核的尺寸不会太大,从而保证能提取到足够小的局部的特征)。这样就会使得后续层的参数空间仍然很大。池化层通过对特征采样,进一步减少了神经元个数。
针对原图进行像素级别的采样,能在保持原图大致内容的前提下,达到图像压缩的目的。池化层也是如此,经过采样,虽然可能丢失一些特征细节,但能保证抓住其中的要点。
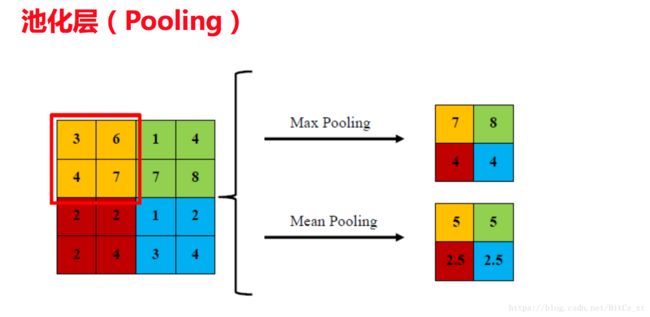
参照上图,左边为特征矩阵,右边为池化后的结果。以黄色框内元素为例, MaxPooling M a x P o o l i n g 取出四个元素中最大的元素,相当于取出了其中特征最鲜明的像素代表,而 AveragePooling A v e r a g e P o o l i n g 均值化了四个元素,则相当于综合考量了这个局部区域的像素特征,其它框进行类似操作。可以看到特征矩阵尺寸缩小为了四分之一,且仍然保持了局部结构的相对不变性(各颜色的框位置是没变的)。这进一步降低了训练计算的开销,且通过引入采样这种带有随机性质的行为,有效地防止了过拟合。
经过以上卷积层、池化层的操作后,像素矩阵被压缩为了一个小尺寸的池化特征矩阵:
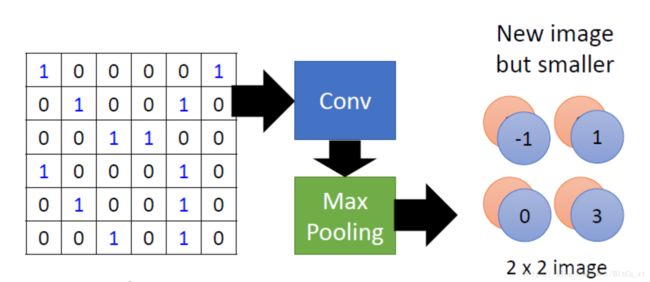
可以想象,被压缩后的池化特征矩阵仍然具有类似于图像的性质,其中的每个元素都来自于特征矩阵的对应区域,而特征矩阵中的元素又来自于原始像素矩阵的各个局部区域。因此,运用深度学习的思想,我们可以堆叠卷积-池化的模块,来让模型变“深”,具备更强的拟合能力。

第一个卷积-池化模块的输出结果是诸如轮廓,边角之类的特征信息,第二个模块在前一个模块的结果上进行进一步的特征提取,得到的便是更细微的特征元素,比如线段、弧度等等。通过数个这样的模块堆叠,将原始像素矩阵逐步拆解为很细微的特征表示,达到表示学习、理解图像的目的。
全连接层
卷积-池化模块已经完成了表示学习部分,全连接层只是充当特征组织与分类的角色。将池化层的高阶特征矩阵打平,输入到全连接层即可。在不同的问题中,按不同方式来配置卷积-池化模块(如调整卷积核大小、个数、初始化方法;池化层尺寸、步长;堆叠层数、激活函数等等),来对不同类型的特征进行提取。根据最终表示学习结果的尺寸,合理设置全连接层的层数、神经元个数,达到分类的目的。