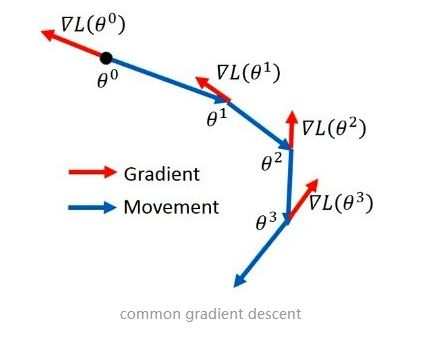
梯度下降优化算法Momentum
一. 基本原理
1.1 引入
Momentum算法在原有的梯度下降法中引入了动量,从物理学上看,引入动量比起普通梯度下降法主要能够增加两个优点。首先,引入动量能够使得物体在下落过程中,当遇到一个局部最优的时候有可能在原有动量的基础上冲出这个局部最优点;并且,普通的梯度下降法方法完全由梯度决定,这就可能导致在寻找最优解的过程中出现严重震荡而速度变慢,但是在有动量的条件下,物体运动方向由动量和梯度共同决定,可以使得物体的震荡减弱,更快地运动到最优解。
1.2 指数加权移动平均
指数加权移动平均是一种常用的序列数据处理方式,用于描述数值的变化趋势,本质上是一种近似求平均的方法。计算公式如下:
v t = β v t − 1 + ( 1 − β ) θ t v_t=\beta v_{t-1}+(1-\beta)\theta_t vt=βvt−1+(1−β)θt
v t v_t vt表示第t个数的估计值, β \beta β为一个可调参数,能表示 v t − 1 v_{t-1} vt−1的权重, θ t \theta_t θt表示第t个数的实际值。
比如,假设有以下余弦函数,并随机添加了一些噪声,

于是,使用指数加权移动平均对这些离散点进行计算,可以对这些离散点进行去噪( β = 0.9 \beta=0.9 β=0.9),于是得到图像:
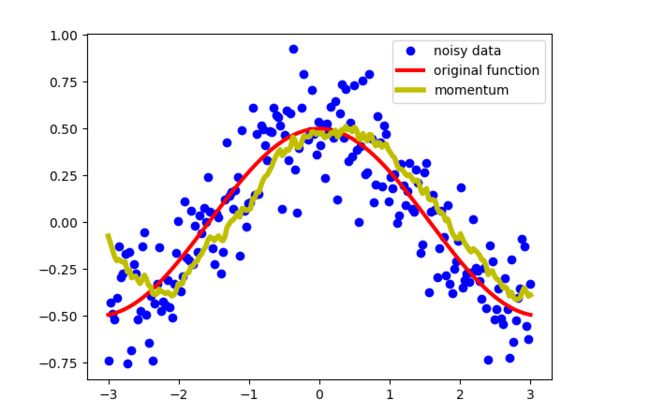
使用指数加权移动平均得到的估计数据能对数据进行去噪,并且得到的数据接近原始功能。
上面进行指数加权移动平均使用的超参数 β = 0.9 \beta=0.9 β=0.9,但是是如何确定的该超参数呢?由原始的公式,设 v 0 = 0 v_0=0 v0=0,得到:
{ v 1 = β v 0 + ( 1 − β ) θ 1 v 2 = β v 1 + ( 1 − β ) θ 2 v 3 = β v 2 + ( 1 − β ) θ 3 \left\{ \begin{array}{rcl} v_1=\beta v_0+(1-\beta)\theta_1 \\ v_2=\beta v_1+(1-\beta)\theta_2 \\ v_3=\beta v_2+(1-\beta)\theta_3 \end{array} \right. ⎩⎨⎧v1=βv0+(1−β)θ1v2=βv1+(1−β)θ2v3=βv2+(1−β)θ3
于是
v n = β v n − 1 + ( 1 − β ) θ n = ( 1 − β ) θ n + β ( 1 − β ) θ n − 1 + β 2 ( 1 − β ) θ n − 2 + . . . + β n − 1 ( 1 − β ) θ 1 v_n=\beta v_{n-1}+(1-\beta)\theta_n=(1-\beta)\theta_n+\beta(1-\beta)\theta_{n-1}+\beta^2(1-\beta)\theta_{n-2}+...+\beta^{n-1}(1-\beta)\theta_1 vn=βvn−1+(1−β)θn=(1−β)θn+β(1−β)θn−1+β2(1−β)θn−2+...+βn−1(1−β)θ1
v n v_n vn为对第n个数的估计值,也是加权平均,由于加权系数随着与第n个数的距离以指数的形式递减,在x方向上越靠近第n个数,权重越大,越远离这个数则权重越小。当 β = 0.9 \beta=0.9 β=0.9时, 0. 9 10 ≈ 0.35 ≈ 1 / e 0.9^{10}\approx0.35\approx1/e 0.910≈0.35≈1/e,如果以1/e为分界点,权值衰减到这个值以下时就忽略不计,则对某个点的指数加权平均求的就是这个数以前最近 N = 1 / ( 1 − β ) = 10 N=1/(1-\beta)=10 N=1/(1−β)=10个数的加权平均值。
当使用不同的 β \beta β值时,对上图的数据点进行估计,结果如下:
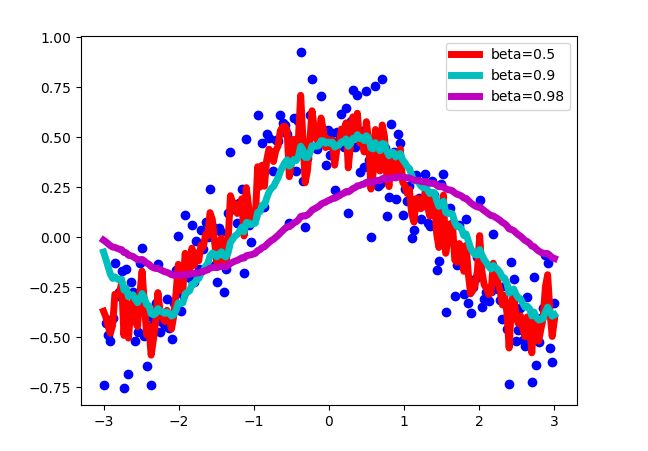
可以见到,当 β \beta β值太大时并不能很好反应总体数据的趋势情况,太小时出现过拟合情况,相邻点间的波动太大,当 β = 0.9 \beta=0.9 β=0.9时,既能反应出原数据的总体趋势,波动又不至于太大。所有在一般的Momentum算法中, β \beta β值一般取0.9。
1.3 Momentum
Momentum就是在普通的梯度下降法中引入指数加权移动平均,即定义一个动量,它是梯度的指数加权移动平均值,然后使用该值代替原来的梯度方向来更新。定义的动量为:
v t = β v t − 1 + ( 1 − β ) ∇ L ( w ) v_t=\beta v_{t-1}+(1-\beta)\nabla L(w) vt=βvt−1+(1−β)∇L(w)
该式中, v t v_t vt表示当前动量, β \beta β就是前文提到的超参数, ∇ L ( w ) \nabla L(w) ∇L(w)为目标函数的当前梯度,使用该动量带入梯度下降公式:
w = w − α v t w=w-\alpha v_t w=w−αvt
该式和普通梯度下降法迭代公式基本一致,只是方向 v t v_t vt是定义的动量, α \alpha α为步长,一般也是一个定义的超参数。
在机器学习中,普通的随机梯度下降法中,由于无法计算损失函数的确切导数,嘈杂的数据会使下降过程并不朝着最佳方向前进,使用加权平均能对嘈杂数据进行一定的屏蔽,使前进方向更接近实际梯度。
另外,随机梯度下降法在局部极小值极有可能被困住,但Momentum由于下降方向由最近的一些数共同决定,能在一定程度反应总体的最佳下降方向,所以在这方面被困在局部最优解的可能会减小。随机梯度下降法和Momentum对比:

二. 程序实现
我以一个简单函数 y = x 1 + 2 x 2 y=x_1+2x_2 y=x1+2x2为例,给定一些训练数据,使用Momentum算法进行训练,确定 x 1 x_1 x1和 x 2 x_2 x2的参数,首先给定8组训练数据并确定相关学习参数:
x = np.array([(1, 1), (1, 2), (2, 2), (3, 1), (1, 3), (2, 4), (2, 3), (3, 3)])
y = np.array([3, 5, 6, 5, 7, 10, 8, 9])
# 初始化
m, dim = x.shape
theta = np.zeros(dim) # 参数
alpha = 0.1 # 学习率
beta = 0.9 # beta
threshold = 0.0001 # 停止迭代的错误阈值
iterations = 1500 # 迭代次数
error = 0 # 初始误差为0
gradient = 0 # 初始梯度为0
随后就是进行学习的过程,学习结束条件为达到最大迭代次数iterations或者总体误差小于阈值threshold。学习过程就是更新参数theta的过程。更新方法就是使用Momentum算法,首先求得动量,求动量的梯度是使用的近似计算,然后进行使用迭代公式更新参数即可,两个公式和前文相同:
v t = β v t − 1 + ( 1 − β ) ∇ L ( w ) v_t=\beta v_{t-1}+(1-\beta)\nabla L(w) vt=βvt−1+(1−β)∇L(w) w = w − α v t w=w-\alpha v_t w=w−αvt
代码实现:
gradient = beta * gradient + (1 - beta) * (x[j] * (np.dot(x[j], theta) - y[j]))
theta -= alpha * gradient
全部代码:
# 带冲量的随机梯度下降SGD Momentum
# 以 y=x1+2*x2为例
import numpy as np
# 多元数据
def momentum():
# 训练集,每个样本有三个分量
x = np.array([(1, 1), (1, 2), (2, 2), (3, 1), (1, 3), (2, 4), (2, 3), (3, 3)])
y = np.array([3, 5, 6, 5, 7, 10, 8, 9])
# 初始化
m, dim = x.shape
theta = np.zeros(dim) # 参数
alpha = 0.1 # 学习率
beta = 0.9 # beta
threshold = 0.0001 # 停止迭代的错误阈值
iterations = 1500 # 迭代次数
error = 0 # 初始误差为0
gradient = 0 # 初始梯度为0
# 迭代开始
for i in range(iterations):
j = i % m
error = 1 / (2 * m) * np.dot((np.dot(x, theta) - y), (np.dot(x, theta) - y))
# 迭代停止
if abs(error) <= threshold:
break
gradient = beta * gradient + (1 - beta) * (x[j] * (np.dot(x[j], theta) - y[j]))
theta -= alpha * gradient
print('迭代次数:%d' % (i + 1), 'theta:', theta, 'error:%f' % error)
if __name__ == '__main__':
momentum()
运行结果:
迭代次数:98 theta: [1.00250137 1.99699225] error:0.000009
可以见到,仅迭代了98次就达到了近似正确结果。
三. 总结
Momentum算法主要的公式只有如下两个,已在前文多次提到:
v t = β v t − 1 + ( 1 − β ) ∇ L ( w ) v_t=\beta v_{t-1}+(1-\beta)\nabla L(w) vt=βvt−1+(1−β)∇L(w) w = w − α v t w=w-\alpha v_t w=w−αvt
Momentum算法在随机梯度下降法的基础上引入动量,能够加速向最优解的迭代,同时能够在一定程度上避免随机梯度下降法的被困在局部最优解。动量的计算是使用指数加权移动平均,使用该动量代替了随机梯度下降法的梯度方向。总体的迭代公式和随机梯度下降法基本相同。
四. 参考文献
[1] Vitaly Bushaev. Stochastic Gradient Descent with momentum. https://towardsdatascience.com/stochastic-gradient-descent-with-momentum-a84097641a5d. 2020.5.29
[2] 不会停的蜗牛. 为什么在优化算法中使用指数加权平均. https://www.jianshu.com/p/41218cb5e099?utm_source=oschina-app. 2020.5. 28