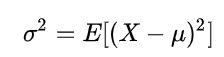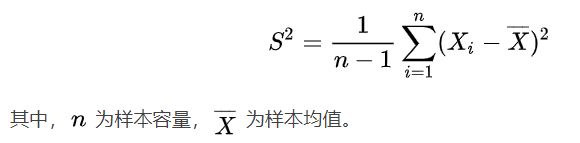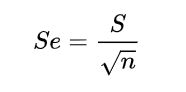我是这样学统计学的，标准差和标准误关系

标准差

标准差是方差的平方根。标准差能反映一个数据集的离散程度，标准偏差越小，这些值偏离平均值就越少，反之亦然。标准偏差的大小可通过标准偏差与平均值的倍率关系来衡量。平均数相同的两个数据集，标准差未必相同。

例如，A、B两组各有6位学生参加同一次语文测验，A组的分数为95、85、75、65、55、45，B组的分数为73、72、71、69、68、67。这两组的平均数都是70，但A组的标准差应该是17.078分,B组的标准差应该是2.160分，说明A组学生之间的差距要比B组学生之间的差距大得多。

总体标准差

已知随机变量 X 的数学期望为μ缪，标准差为σ西格玛，则其方差为：

此处σ即为随机变量X的总体标准差。

样本标准差

上面的式子中，我们需要准确的了解随机变量 X的总体分布，从而可以计算出其总体的期望和标准差。

但在一般情况下，对总体的每一个个体都进行观察或试验是不可能的。因此，必须对总体进行抽样观察（采样）。由于我们是利用抽样来对总体的分布进行推断，所以抽样必须是随机的，抽样值

应视为一组随机变量。由于抽样的目的是为了对总体的分布进行统计推断，为了使抽取的样本能很好地反映总体信息，必须考虑抽样方法。最常用的一种抽样方法叫作 “简单随机抽样”，得到的样本称为简单随机样本，它要求抽取的样本满足以下两点：

代表性：抽样值中每一个与所考察的总体有相同的分布。

独立性：抽样值是相互独立的随机变量。

满足以上两点要求的样本一般被称为独立同分布independent and identically distributed (i.i.d.)样本。

在概率统计理论中，如果变量序列或者其他随机变量有相同的概率分布，并且互相独立，那么这些随机变量是独立同分布。 在西瓜书中的解释是：输入空间中的所有样本服从一个隐含未知的分布，训练数据所有样本都是独立地从这个分布上采样而得。

所以在实践中采样得到i.i.d.样本之后，可以用样本方差S平方来近似总体方差σ平方。

疑问？？？为什么样本方差的分母是n-1？为什么它又叫做无偏估计？

答案在这里：为什么样本方差的分母是n-1？为什么它又叫做无偏估计？_图灵的猫i的博客-CSDN博客_样本方差为什么是n-1

标准误

例如：已知某学校有初三学生共200名，这200名学生的平均身高为160cm.我们以这200名初三学生作为总体，欲通过抽样调查来了解所有初三学生的平均身高。现在假定我们共做了10次抽样，每次抽样量都是100人。此时我们可以分别计算出每次抽样样本的身高均数和标准差，可以得到10个均数和标准差。这里10个均数和标准差都是样本统计量，如果我们把10个样本的均数作为原始数据，然后计算这10个值的标准差，那么我们得到的指标就是标准误。

它们针对计算的对象不同。标准差是根据某次抽样的原始数据计算的；而标准误是根据多次抽样的样本统计量（如均数、率等）计算的。理论上，计算标准差只需要一个样本，而计算标准误需要多个样本。

尽管从理论上来讲，标准误的计算是通过多次抽样的多个样本统计量而获得的，但在实际中仅依靠一次抽样来计算标准误也是可行的。事实上，在绝大多数情况下，我们也别无选择，只能利用一次抽样数据来计算标准误。此时标准误的计算公式为：

其中，s表示样本标准差，n为样本的例数。不难看出，样本例数越大，标准误越小，即抽样误差越小。

标准差与标准误

联系：

二者都是标准差。

标准误=标准差 / N的根号。标准误差定义为各测量值误差的平方和的平均值的平方根，故又称为均方根误差。

区别：

标准误是一种误差。

标准差是对均数的偏离。

偏离和误差根本不是一个概念。

随机变量的标准差衡量的是该随机变量的离散度。例如：一个样本或者一个population里的个体之间区别有多大。

标准误即样本均数的标准差，是描述均数抽样分布的离散程度及衡量均数抽样误差大小的尺度，反映的是样本均数之间的变异。标准误不是标准差，是多个样本平均数的标准差。标准误用来衡量抽样误差。

标准误是样本统计量的标准差，衡量的是抽样分布的离散度，对应的随机变量是样本统计量。比如样本均值的标准误，衡量的就是样本均值的离散度。例如：从一个population 里取样本，样本之间的区别有多大。

标准误越小，表明样本统计量与总体参数的值越接近，样本对总体越有代表性，用样本统计量推断总体参数的可靠度越大。因此，标准误是统计推断可靠性的指标。

标准差：一次抽样中个体分数间的离散程度，反映了个体分数对样本均值的代表性，用于描述统计。

标准误： 多次抽样中样本均值间的离散程度，反映了样本均值对总体均值的代表性，用于推论统计。

标准差是一个描述性指标，只是描述原始数据的波动情况。而标准误是跟统计推断有关的指标。描述性指标和推论性指标不是一个概念。

标准差	标准误
区别	1.意义：描述个人观察值变异程度的大小。标准差小， 公卫百科                 均数对一组观察值的代表性好。 2.应用：与均数结合，用以描述个人观察值的范围，常                用于医学参考范围的估计。 公卫论坛 3.与n的关系：n越大，标准差越趋于稳定。	描述样本均数的变异程度及抽样误差的大小，其实质是 公卫家园 样本均数的标准差。标准误小，用样本均数推断总体均 数的可能性大 。 与均数结合，用以估计总体均数可能出现的范围以及对 公卫人 总体均数作假设检验。 n越大，标准误下降。
联系	1. 都是描述变异程度的指标     2.  由公式可知，标准差与标准误成正比， 公卫家园           n一定时，标准差越大，标准误越大

标准差与标准误的变量：

标准差：描述个体值间的变异(抽样误差)，标准差较小，表示观察值围绕均数的波动较小，说明样本均数的代表性就越好。 标 准误：描述样本均数的抽样误差，标准误较小，表示样本均数与总体均数较接近。说明样本均数的可靠性。
标准差：表示变量值离散程度的大小，结合均数估计参考值范围。 公卫考场
标准误：表示抽样误差的大小，估计总体均数的可信区间。
标准差：随样本含量的增多，逐渐趋于稳定
标准误：随样本含量的增多逐渐减小。
标准差与标准误都是变异指标，说明个体值之间差异是用标准差，说明样本均数之间差异时用标准误。当样本含量不变时，标准差越大，标准误越大。