Python科学计算:Sympy
今天到了计算机代数系统(CAS)这一块了,说实话,这个Sympy我还真的从来没用过,咱也不知道人这个咋用,所以,对这个软件包的学习,咱还是牢牢地跟着书上的讲解走吧。
首先,请出我们的老朋友:
pip install Sympy这样,电脑上就算是成功安装好了Sympy,然后,导入这个包也很简单:
import sympy as sy好了这下就开始学习吧:
符号和函数
我们书写的代数式子,是不能在Sympy中正常使用的,因为他不符合Python的语法规则,举个例子
![]()
他就没有办法在Sympy中运行,因为我们没有定义标识符x,y这俩值,而我们又是希望他们可以是任意值,这个时候,Sympy提出的解决方案是定义一个行的实体:一个符号,实际上是一个Python类,按下面的方式进行即可:
import sympy as sp
x,y=sp.symbols("x y")
D=(x+y)*sp.exp(x)*sp.cos(y)
print(D)然后,我们来看一看结果(图二):
这里讲个问题,不同的IDE,输出的方式可能是不一样的,就比如说,我用的Pycharm、VsCode、Jupyter-lab,这三个你就得print输出,然而,有些书上讲的,不用Print函数,直接就是D,这种一般在用Ipython的时候会这么写,应该是不同IDE的问题,但是不打紧。
在这里,我们从来没有声明说D是一个符号,因为这样做没必要,根据定义,D继承了赋值语句右侧的所有属性,而D赋值右测本来就是一个符号,Python只需要把标识符D和这个符号对象关联起来就行。
如上面,D是一个已知的关于x和y的函数,我们通常是需要未知函数的,比如说:![]() ,
,
![]() 这类的未知函数,未知函数是可以通过向sp.symbols传递额外的关键字参数来创建的(如图三)
这类的未知函数,未知函数是可以通过向sp.symbols传递额外的关键字参数来创建的(如图三)
f,g=sp.symbols("f g",cls=sp.Function)
print(f(x))
print(f(x,y))
print(g(x))
CAUTION!!!,Sympy不知道也不关心函数参数的数量,检查参数值的一致性是用户的责任,
i,j=sp.symbols("i j",integer=True)
u,v=sp.symbols("u v",real=True)
print(i.is_integer)
print(j*j)
print((j*j).is_integer)
print(u.is_real)在Sympy中,符号实际上是类的实例,他们是具有属性的。
在Sympy中,![]() 不是用i或者j来表示的,他有专门的表示:Sympy.I,同样的,我们有很多有用的,比如说,e、pi、无群大这几个,在Sympy中各表示为:Sympy.E,Sympy.pi,Sympy.oo
不是用i或者j来表示的,他有专门的表示:Sympy.I,同样的,我们有很多有用的,比如说,e、pi、无群大这几个,在Sympy中各表示为:Sympy.E,Sympy.pi,Sympy.oo
怎样找出用特定值代替D中的x和y的结果?
使用替换操作来实现,替换操作既可以作为函数Sympy.subs(),也可以作为类方法来使用,后者有时候用的更为广泛:
D0=D.subs(x,0)
D0pi=D0.subs(y,sp.pi)
print(D0,D0pi,D.subs([(x,0),(y,sp.pi)]))第一行代码中的替换操作不会改变D的!!!
Python和Sympy之间的转换
我们延续之前的设定,x,y这两个符号,所以这里![]() ,
,![]() 这些都是符号,整数和浮点数自动扩展转换成符号,分数的话则需要注意一下,我们来看这样一段代码:
这些都是符号,整数和浮点数自动扩展转换成符号,分数的话则需要注意一下,我们来看这样一段代码:
print(x+1/3)但是这里会发现一个非常让人头疼的问题,输出是x+0.333333333333333333这样的,这和我们险要的并不太符合,那么,我们采取以下的一种策略:
print(x+sp.Rational(1,3))
print(sp.Rational('0.5')*y)这下来看看输出结果:
我们还可以,用sp.s函数把给定的字符表达式作为参数,结果在转换成等价的Sympy表达式:
print(x+sp.S('1/3'))
print(sp.S('0.5')*y)同时,我们还可以用sp.sympify()函数来讲给定的任意表达式字符参数转换成预期等价的Sympy表达式:
D_s=sp.sympify("(x+y)*exp(x)*cos(y)")
cosdiff=sp.sympify("cos(x)*cos(y)-sin(x)*sin(y)")
print(D_s)
print(cosdiff)在上面代码中D_S的效果相当于前面的D。
如果我们只需要几个显式值,那么上面提到的函数subs就会提供他们的符号值,我们可以用sp.evalf函数来获得数值,他可以带一个整数参数作为精度单位,SP.N也是实现了sp.evalf的大多数功能,说到这里,我就不理解了,一个包里面,要两个功能基本上算是一毛一样的函数干啥啊,他不冗余吗?
cospi4=cosdiff.subs([(x,sp.pi/2),(y,sp.pi/4)])
print(cospi4)
print(cospi4.evalf())
print(cospi4.evalf(6))
print(sp.N(cospi4,6))可以看到,精度是6位的输出结果中,这两个函数实现的结果是一模一样的。
我们再跟着书上的例子来一个:
import numpy as np
func=sp.lambdify((x,y),cosdiff,"numpy")
xn=np.linspace(0,np.pi,13)
print(func(xn,0.0))这段代码,其实就是说,我要生成一个数组,而且这个数组石油一定规律的,那这个规律是啥呢,就是cosdiff,实际上我们可以看到,他就是![]() 。再加上他的图像:
。再加上他的图像:
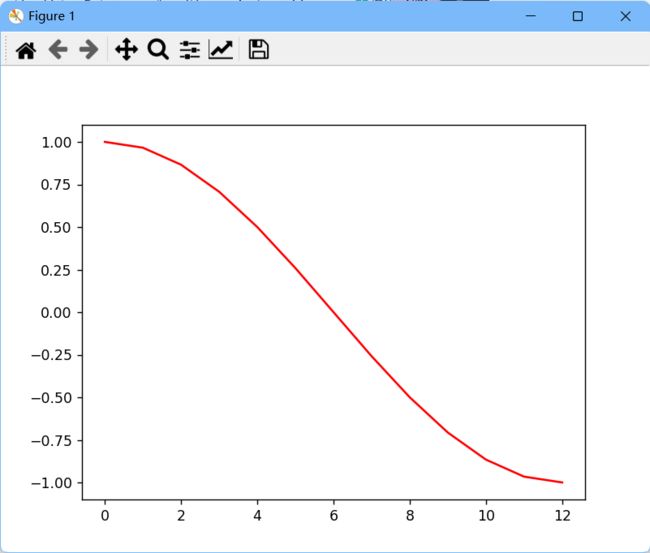
其实,我们如果说想更加直观的看到![]() 的图像到底是什么样子的(上面那个不清楚),就可以修改参数:
的图像到底是什么样子的(上面那个不清楚),就可以修改参数:
xn=np.linspace(0,10*np.pi,1000)这下,就可以看的非常清晰明了了。
矩阵和向量:
Sympy用Matrix类来实现矩阵,并且讲n个元素的向量作为![]() 矩阵,构造函数需要一个有序的行列表,其中,每一行是元素有序列表,来看着做吧:
矩阵,构造函数需要一个有序的行列表,其中,每一行是元素有序列表,来看着做吧:
M=sp.Matrix([[1,x],[y,1]])
N=sp.Matrix([[u],[v]])
print(M)
print(N)
print(M*N)QAQ,Python的这个语法就,就很让人烦,()里面还得放[],[]里面才能再加[],我想了半天哪不对劲,原来在这,就和上次numpy的zeros一样,半天老是报错,找原因找了半天,才发现是这里的错误,唉,就这个事情有些不银性化。
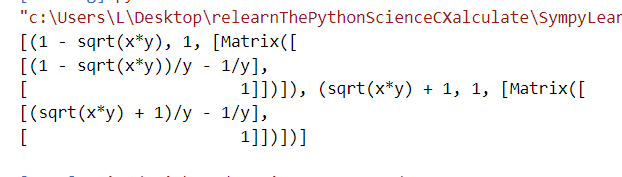
我们可以用eigenvects函数,来返回一个元组的列表,其中每个元组都包含着特征向量的特征值、多重数、基数:
然后嘞,我们可以很简单的对方阵进行转置、行列式、求逆等:
#转置
M.T
#行列式
M.det()
#求逆
M.inv()
#正逆相乘
M*M.inv()注意,已经定义好的矩阵M是不可以变得(这里指的是他的阶数),但是他的内容是完全可以自由改变的,比如说,我们试着改一下看看:
M=sp.Matrix([[1,x],[y,1]])
print(M)
M[0,1]=u
print(M)ok这里就结束了,其实还是我上次写的,对于编程来说,书上写的都是些皮毛,看着今天写了这么多,其实来来回回就那么几个函数,可是嘞,当我们去查看文档的时候,文档里面的函数多的就离谱,所以光靠书本还是不够的,Python的基础语法,看看书还行,但是,一旦我们有更高的要求的时候,文档还是最好的学习选择,所以,这里附上Sympy的文档,大家闲了有时间可以去看一看:SymPy 1.11 文档