【Matlab】基于粒子群优化算法优化BP神经网络的数据分类预测

1.模型原理

“基于粒子群优化算法优化BP神经网络的数据分类预测”是一种结合了粒子群优化算法（Particle Swarm Optimization, PSO）和BP神经网络进行数据分类预测任务的方法。PSO是一种全局优化算法，能够帮助BP神经网络更好地优化权重和偏置，从而提高分类预测性能。该方法通过优化BP神经网络的参数，使其能够更准确地将输入数据样本映射到相应的类别标签。

以下是“基于粒子群优化算法优化BP神经网络的数据分类预测”的原理：

1. BP神经网络简介：
   BP神经网络是一种前向人工神经网络，由输入层、若干隐藏层和输出层组成。它通过前向传播计算输出，并通过反向传播算法来更新权重和偏置，以最小化预测值与真实值之间的误差。BP神经网络在数据分类预测问题中可以用于拟合非线性函数，并通过梯度下降法进行参数优化。

2. 粒子群优化算法简介：
   PSO是一种群体智能优化算法，受到鸟群觅食行为的启发。在PSO中，个体被称为“粒子”，它们在搜索空间中移动，并通过学习社会最优和个体最优位置来更新自己的位置和速度。每个粒子维护两个向量：速度向量和位置向量，它们决定了粒子在搜索空间中的移动方向和距离。

3. 基于粒子群优化的BP神经网络优化：
   在使用PSO优化BP神经网络时，我们将BP神经网络的权重和偏置作为待优化的参数。每个粒子表示一组可能的权重和偏置的取值，称为“粒子的位置”。PSO算法中的每个粒子都有一个适应度函数，用于评估其在数据分类预测任务中的表现。在这里，适应度函数可以是分类预测任务中的准确率或交叉熵损失函数。

4. PSO算法流程：
   PSO算法的基本流程如下：

   • 初始化粒子群的位置和速度。
   • 计算每个粒子的适应度值（即BP神经网络在训练数据上的预测准确率或损失）。
   • 根据个体最优和全局最优位置更新粒子的速度和位置。
   • 重复上述步骤，直到满足停止条件（如达到最大迭代次数或达到预定的精度）。

5. 优化过程：
   在优化过程中，每个粒子代表了一组BP神经网络的权重和偏置。它们根据自身的适应度和周围粒子的表现来更新自己的位置和速度，以寻找更优的权重和偏置组合。通过迭代优化，粒子逐渐趋向于全局最优解，从而找到了最优的BP神经网络权重和偏置组合，以提高数据分类预测的性能。

6. 应用于数据分类预测：
   将PSO算法与BP神经网络结合应用于数据分类预测任务时，首先需要准备训练数据和测试数据。然后，利用PSO算法优化BP神经网络的权重和偏置，使其能够更好地拟合训练数据。最后，使用优化后的BP神经网络对测试数据进行预测，得到数据的分类结果。

通过以上的优化过程，基于粒子群优化算法优化BP神经网络的数据分类预测方法可以帮助BP神经网络更好地适应数据分类任务，提高预测准确率，并在实际应用中取得更好的分类性能。

2.数学公式

当然可以！在下面，我将详细介绍“基于粒子群优化算法优化BP神经网络的数据分类预测”的原理，并带上公式：

1. BP神经网络部分：

假设我们有一个数据集 ($D$)，其中包含 ($N$) 个样本： $D=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}$，其中 ($x_i$) 是第 ($i$) 个样本的输入特征， ($y_i$) 是对应的标签。

在BP神经网络中，我们使用前向传播计算隐藏层和输出层的输出，然后使用反向传播算法来更新权重和偏置，以最小化预测值与真实值之间的误差。隐藏层和输出层的计算公式如下：

隐藏层的计算公式：
$z_h=W_{xh}\cdot x+b_h$
$h=\sigma (z_h)$

输出层的计算公式：
$z_o=W_{ho}\cdot h+b_o$
$y=\sigma (z_o)$

其中，

• ($h$) 是隐藏层的输出（隐藏状态），
• ($y$) 是输出层的输出（预测值），
• ($W_{xh}$) 是输入到隐藏层的权重矩阵，
• ($W_{ho}$) 是隐藏层到输出层的权重矩阵，
• ($b_h$) 是隐藏层的偏置，
• ($b_o$) 是输出层的偏置，
• ($\sigma$) 是激活函数（如sigmoid或tanh）。

2. 粒子群优化算法部分：

在粒子群优化算法中，每个粒子代表一组可能的BP神经网络的权重和偏置，即一组解。这些粒子在搜索空间中移动，并通过学习社会最优和个体最优位置来更新自己的位置和速度。每个粒子维护两个向量：速度向量和位置向量，它们决定了粒子在搜索空间中的移动方向和距离。

假设第 ($i$) 个粒子在当前时刻的位置向量为 ($x_i$)，速度向量为 ($v_i$)，个体最优位置为 ($p_i$)，全局最优位置为 ($p_g$)。

粒子更新的公式为：
$v_i(t+1)=\omega \cdot v_i(t)+c_1\cdot r_1\cdot (p_i-x_i(t))+c_2\cdot r_2\cdot (p_g-x_i(t))$
$x_i(t+1)=x_i(t)+v_i(t+1)$

其中，

• ($t$) 是当前时刻，
• ($\omega$) 是惯性权重，控制粒子的惯性，
• ($c_1$) 和 ($c_2$) 是学习因子，分别控制个体和全局的权重，
• ($r_1$) 和 ($r_2$) 是随机数，用于增加随机性。

在每一次迭代中，通过计算每个粒子的适应度（即BP神经网络在训练数据上的预测准确率或损失），找到个体最优位置 ($p_i$) 和全局最优位置 ($p_g$)，并更新粒子的速度和位置，直到达到停止条件（如达到最大迭代次数或达到预定的精度）为止。

3. 数据分类预测：

在完成粒子群优化过程后，每个粒子都代表了一组优化后的BP神经网络的权重和偏置。我们可以选择具有最佳适应度的粒子所代表的BP神经网络作为最终的分类器。

将新的输入数据样本 ($x_{\text{new}}$) 输入该BP神经网络，通过前向传播计算输出的隐藏层和输出层的输出，得到预测值 ($y_{\text{pred}}$)。根据预测值 ($y_{\text{pred}}$) 和分类标签 ($y_{\text{true}}$)（来自测试数据集）的对比，我们可以计算分类的准确率或损失，用于评估优化后的BP神经网络在测试数据上的表现。

通过以上的BP神经网络运算、粒子群优化和数据分类预测过程，我们可以实现“基于粒子群优化算法优化BP神经网络的数据分类预测”。这种方法结合了全局优化算法PSO和BP神经网络，能够帮助BP神经网络更好地适应数据分类任务，提高分类准确率，并在实际应用中取得更好的分类性能。

3.文件结构

fun.m							% 适应度值函数
main.m							% 主函数
数据集.xlsx						% 可替换数据集

4.Excel数据

5.分块代码

5.1 fun.m

function error = fun(pop, hiddennum, net, p_train, t_train)

%% 节点个数

inputnum  = size(p_train, 1);  % 输入层节点数
outputnum = size(t_train, 1);  % 输出层节点数

%% 提取权值和阈值

w1 = pop(1 : inputnum * hiddennum);
B1 = pop(inputnum * hiddennum + 1 : inputnum * hiddennum + hiddennum);
w2 = pop(inputnum * hiddennum + hiddennum + 1 : ...
    inputnum * hiddennum + hiddennum + hiddennum * outputnum);
B2 = pop(inputnum * hiddennum + hiddennum + hiddennum * outputnum + 1 : ...
    inputnum * hiddennum + hiddennum + hiddennum * outputnum + outputnum);

%% 网络赋值

net.Iw{1, 1} = reshape(w1, hiddennum, inputnum );
net.Lw{2, 1} = reshape(w2, outputnum, hiddennum);
net.b{1}     = reshape(B1, hiddennum, 1);
net.b{2}     = B2';

%% 网络训练

net = train(net, p_train, t_train);

%% 仿真测试

t_sim1 = sim(net, p_train);

%% 反归一化

T_sim1  = vec2ind(t_sim1 );
T_train = vec2ind(t_train);

%% 适应度值

error = 1 - sum(T_sim1 == T_train) / length(T_sim1);

5.2 main.m

%% 清空环境变量

warning off             % 关闭报警信息
close all               % 关闭开启的图窗
clear                   % 清空变量
clc                     % 清空命令行

%% 导入数据

res = xlsread('数据集.xlsx');

%% 划分训练集和测试集

temp = randperm(357);

P_train = res(temp(1: 240), 1: 12)';
T_train = res(temp(1: 240), 13)';
M = size(P_train, 2);

P_test = res(temp(241: end), 1: 12)';
T_test = res(temp(241: end), 13)';
N = size(P_test, 2);

%% 数据归一化

[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test  = mapminmax('apply', P_test, ps_input);
t_train = ind2vec(T_train);
t_test  = ind2vec(T_test );

%% 节点个数

inputnum  = size(p_train, 1);  % 输入层节点数
hiddennum = 6;                 % 隐藏层节点数
outputnum = size(t_train,1);   % 输出层节点数

%% 建立网络

net = newff(p_train, t_train, hiddennum);

%% 设置训练参数

net.trainParam.epochs     = 1000;      % 训练次数
net.trainParam.goal       = 1e-5;      % 目标误差
net.trainParam.lr         = 0.01;      % 学习率
net.trainParam.showWindow = 0;         % 关闭窗口

%% 参数初始化

c1      = 4.494;       % 学习因子
c2      = 4.494;       % 学习因子
maxgen  =   30;        % 种群更新次数  
sizepop =    5;        % 种群规模
Vmax    =  1.0;        % 最大速度
Vmin    = -1.0;        % 最小速度
popmax  =  2.0;        % 最大边界
popmin  = -2.0;        % 最小边界

%% 节点总数

numsum = inputnum * hiddennum + hiddennum + hiddennum * outputnum + outputnum;

for i = 1 : sizepop
    pop(i, :) = rands(1, numsum);  % 初始化种群
    V(i, :) = rands(1, numsum);    % 初始化速度
    fitness(i) = fun(pop(i, :), hiddennum, net, p_train, t_train);
end

%% 个体极值和群体极值

[fitnesszbest, bestindex] = min(fitness);
zbest = pop(bestindex, :);     % 全局最佳
gbest = pop;                   % 个体最佳
fitnessgbest = fitness;        % 个体最佳适应度值
BestFit = fitnesszbest;        % 全局最佳适应度值

%% 迭代寻优

for i = 1 : maxgen
    for j = 1 : sizepop
        
        % 速度更新
        V(j, :) = V(j, :) + c1 * rand * (gbest(j, :) - pop(j, :)) + c2 * rand * (zbest - pop(j, :));
        V(j, (V(j, :) > Vmax)) = Vmax;
        V(j, (V(j, :) < Vmin)) = Vmin;
        
        % 种群更新
        pop(j, :) = pop(j, :) + 0.2 * V(j, :);
        pop(j, (pop(j, :) > popmax)) = popmax;
        pop(j, (pop(j, :) < popmin)) = popmin;
        
        % 自适应变异
        pos = unidrnd(numsum);
        if rand > 0.95
            pop(j, pos) = rands(1, 1);
        end
        
        % 适应度值
        fitness(j) = fun(pop(j, :), hiddennum, net, p_train, t_train);

    end
    
    for j = 1 : sizepop

        % 个体最优更新
        if fitness(j) < fitnessgbest(j)
            gbest(j, :) = pop(j, :);
            fitnessgbest(j) = fitness(j);
        end

        % 群体最优更新 
        if fitness(j) < fitnesszbest
            zbest = pop(j, :);
            fitnesszbest = fitness(j);
        end

    end

    BestFit = [BestFit, fitnesszbest];    
end

%% 提取最优初始权值和阈值

w1 = zbest(1 : inputnum * hiddennum);
B1 = zbest(inputnum * hiddennum + 1 : inputnum * hiddennum + hiddennum);
w2 = zbest(inputnum * hiddennum + hiddennum + 1 : inputnum * hiddennum ...
    + hiddennum + hiddennum * outputnum);
B2 = zbest(inputnum * hiddennum + hiddennum + hiddennum * outputnum + 1 : ...
    inputnum * hiddennum + hiddennum + hiddennum * outputnum + outputnum);

%% 网络赋值

net.Iw{1, 1} = reshape(w1, hiddennum, inputnum );
net.Lw{2, 1} = reshape(w2, outputnum, hiddennum);
net.b{1}     = reshape(B1, hiddennum, 1);
net.b{2}     = B2';

%% 打开训练窗口

net.trainParam.showWindow = 1;        % 打开窗口

%% 网络训练

net = train(net, p_train, t_train);

%% 仿真预测

t_sim1 = sim(net, p_train);
t_sim2 = sim(net, p_test );

%% 数据反归一化

T_sim1 = vec2ind(t_sim1);
T_sim2 = vec2ind(t_sim2);

%% 数据排序

[T_train, index_1] = sort(T_train);
[T_test , index_2] = sort(T_test );

T_sim1 = T_sim1(index_1);
T_sim2 = T_sim2(index_2);

%% 性能评价

error1 = sum((T_sim1 == T_train)) / M * 100 ;
error2 = sum((T_sim2 == T_test )) / N * 100 ;

%% 绘图

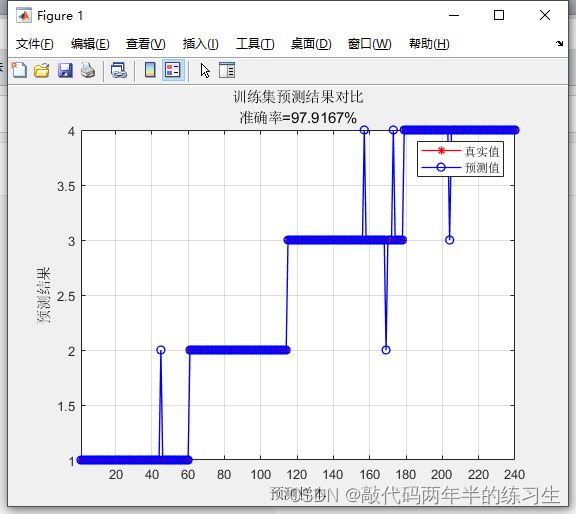
figure
plot(1: M, T_train, 'r-*', 1: M, T_sim1, 'b-o', 'LineWidth', 1)
legend('真实值', '预测值')
xlabel('预测样本')
ylabel('预测结果')
string = {'训练集预测结果对比'; ['准确率=' num2str(error1) '%']};
title(string)
xlim([1, M])
grid

figure
plot(1: N, T_test, 'r-*', 1: N, T_sim2, 'b-o', 'LineWidth', 1)
legend('真实值', '预测值')
xlabel('预测样本')
ylabel('预测结果')
string = {'测试集预测结果对比'; ['准确率=' num2str(error2) '%']};
title(string)
xlim([1, N])
grid

%% 误差曲线迭代图

figure
plot(1 : length(BestFit), BestFit, 'LineWidth', 1.5);
xlabel('粒子群迭代次数');
ylabel('适应度值');
xlim([1, length(BestFit)])
string = {'模型迭代误差变化'};
title(string)

%% 混淆矩阵

figure
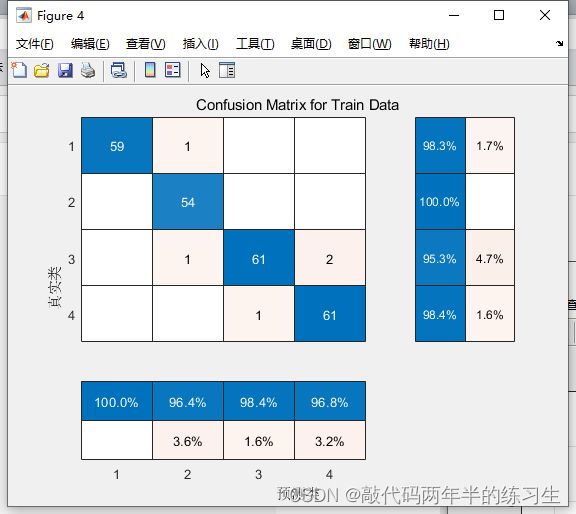
cm = confusionchart(T_train, T_sim1);
cm.Title = 'Confusion Matrix for Train Data';
cm.ColumnSummary = 'column-normalized';
cm.RowSummary = 'row-normalized';
    
figure
cm = confusionchart(T_test, T_sim2);
cm.Title = 'Confusion Matrix for Test Data';
cm.ColumnSummary = 'column-normalized';
cm.RowSummary = 'row-normalized';

6.完整代码

6.1 fun.m

function error = fun(pop, hiddennum, net, p_train, t_train)

%%  节点个数
inputnum  = size(p_train, 1);  % 输入层节点数
outputnum = size(t_train, 1);  % 输出层节点数

%%  提取权值和阈值
w1 = pop(1 : inputnum * hiddennum);
B1 = pop(inputnum * hiddennum + 1 : inputnum * hiddennum + hiddennum);
w2 = pop(inputnum * hiddennum + hiddennum + 1 : ...
    inputnum * hiddennum + hiddennum + hiddennum * outputnum);
B2 = pop(inputnum * hiddennum + hiddennum + hiddennum * outputnum + 1 : ...
    inputnum * hiddennum + hiddennum + hiddennum * outputnum + outputnum);

%%  网络赋值
net.Iw{1, 1} = reshape(w1, hiddennum, inputnum );
net.Lw{2, 1} = reshape(w2, outputnum, hiddennum);
net.b{1}     = reshape(B1, hiddennum, 1);
net.b{2}     = B2';

%%  网络训练
net = train(net, p_train, t_train);

%%  仿真测试
t_sim1 = sim(net, p_train);

%%  反归一化
T_sim1  = vec2ind(t_sim1 );
T_train = vec2ind(t_train);

%%  适应度值
error = 1 - sum(T_sim1 == T_train) / length(T_sim1);

6.2 main.m

%%  清空环境变量
warning off             % 关闭报警信息
close all               % 关闭开启的图窗
clear                   % 清空变量
clc                     % 清空命令行

%%  导入数据
res = xlsread('数据集.xlsx');

%%  划分训练集和测试集
temp = randperm(357);

P_train = res(temp(1: 240), 1: 12)';
T_train = res(temp(1: 240), 13)';
M = size(P_train, 2);

P_test = res(temp(241: end), 1: 12)';
T_test = res(temp(241: end), 13)';
N = size(P_test, 2);

%%  数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test  = mapminmax('apply', P_test, ps_input);
t_train = ind2vec(T_train);
t_test  = ind2vec(T_test );

%%  节点个数
inputnum  = size(p_train, 1);  % 输入层节点数
hiddennum = 6;                 % 隐藏层节点数
outputnum = size(t_train,1);   % 输出层节点数

%%  建立网络
net = newff(p_train, t_train, hiddennum);

%%  设置训练参数
net.trainParam.epochs     = 1000;      % 训练次数
net.trainParam.goal       = 1e-5;      % 目标误差
net.trainParam.lr         = 0.01;      % 学习率
net.trainParam.showWindow = 0;         % 关闭窗口

%%  参数初始化
c1      = 4.494;       % 学习因子
c2      = 4.494;       % 学习因子
maxgen  =   30;        % 种群更新次数  
sizepop =    5;        % 种群规模
Vmax    =  1.0;        % 最大速度
Vmin    = -1.0;        % 最小速度
popmax  =  2.0;        % 最大边界
popmin  = -2.0;        % 最小边界

%%  节点总数
numsum = inputnum * hiddennum + hiddennum + hiddennum * outputnum + outputnum;

for i = 1 : sizepop
    pop(i, :) = rands(1, numsum);  % 初始化种群
    V(i, :) = rands(1, numsum);    % 初始化速度
    fitness(i) = fun(pop(i, :), hiddennum, net, p_train, t_train);
end

%%  个体极值和群体极值
[fitnesszbest, bestindex] = min(fitness);
zbest = pop(bestindex, :);     % 全局最佳
gbest = pop;                   % 个体最佳
fitnessgbest = fitness;        % 个体最佳适应度值
BestFit = fitnesszbest;        % 全局最佳适应度值

%%  迭代寻优
for i = 1 : maxgen
    for j = 1 : sizepop
        
        % 速度更新
        V(j, :) = V(j, :) + c1 * rand * (gbest(j, :) - pop(j, :)) + c2 * rand * (zbest - pop(j, :));
        V(j, (V(j, :) > Vmax)) = Vmax;
        V(j, (V(j, :) < Vmin)) = Vmin;
        
        % 种群更新
        pop(j, :) = pop(j, :) + 0.2 * V(j, :);
        pop(j, (pop(j, :) > popmax)) = popmax;
        pop(j, (pop(j, :) < popmin)) = popmin;
        
        % 自适应变异
        pos = unidrnd(numsum);
        if rand > 0.95
            pop(j, pos) = rands(1, 1);
        end
        
        % 适应度值
        fitness(j) = fun(pop(j, :), hiddennum, net, p_train, t_train);

    end
    
    for j = 1 : sizepop

        % 个体最优更新
        if fitness(j) < fitnessgbest(j)
            gbest(j, :) = pop(j, :);
            fitnessgbest(j) = fitness(j);
        end

        % 群体最优更新 
        if fitness(j) < fitnesszbest
            zbest = pop(j, :);
            fitnesszbest = fitness(j);
        end

    end

    BestFit = [BestFit, fitnesszbest];    
end

%%  提取最优初始权值和阈值
w1 = zbest(1 : inputnum * hiddennum);
B1 = zbest(inputnum * hiddennum + 1 : inputnum * hiddennum + hiddennum);
w2 = zbest(inputnum * hiddennum + hiddennum + 1 : inputnum * hiddennum ...
    + hiddennum + hiddennum * outputnum);
B2 = zbest(inputnum * hiddennum + hiddennum + hiddennum * outputnum + 1 : ...
    inputnum * hiddennum + hiddennum + hiddennum * outputnum + outputnum);

%%  网络赋值
net.Iw{1, 1} = reshape(w1, hiddennum, inputnum );
net.Lw{2, 1} = reshape(w2, outputnum, hiddennum);
net.b{1}     = reshape(B1, hiddennum, 1);
net.b{2}     = B2';

%%  打开训练窗口 
net.trainParam.showWindow = 1;        % 打开窗口

%%  网络训练
net = train(net, p_train, t_train);

%%  仿真预测
t_sim1 = sim(net, p_train);
t_sim2 = sim(net, p_test );

%%  数据反归一化
T_sim1 = vec2ind(t_sim1);
T_sim2 = vec2ind(t_sim2);

%%  数据排序
[T_train, index_1] = sort(T_train);
[T_test , index_2] = sort(T_test );

T_sim1 = T_sim1(index_1);
T_sim2 = T_sim2(index_2);

%%  性能评价
error1 = sum((T_sim1 == T_train)) / M * 100 ;
error2 = sum((T_sim2 == T_test )) / N * 100 ;

%%  绘图
figure
plot(1: M, T_train, 'r-*', 1: M, T_sim1, 'b-o', 'LineWidth', 1)
legend('真实值', '预测值')
xlabel('预测样本')
ylabel('预测结果')
string = {'训练集预测结果对比'; ['准确率=' num2str(error1) '%']};
title(string)
xlim([1, M])
grid

figure
plot(1: N, T_test, 'r-*', 1: N, T_sim2, 'b-o', 'LineWidth', 1)
legend('真实值', '预测值')
xlabel('预测样本')
ylabel('预测结果')
string = {'测试集预测结果对比'; ['准确率=' num2str(error2) '%']};
title(string)
xlim([1, N])
grid

%%  误差曲线迭代图
figure
plot(1 : length(BestFit), BestFit, 'LineWidth', 1.5);
xlabel('粒子群迭代次数');
ylabel('适应度值');
xlim([1, length(BestFit)])
string = {'模型迭代误差变化'};
title(string)

%%  混淆矩阵
figure
cm = confusionchart(T_train, T_sim1);
cm.Title = 'Confusion Matrix for Train Data';
cm.ColumnSummary = 'column-normalized';
cm.RowSummary = 'row-normalized';
    
figure
cm = confusionchart(T_test, T_sim2);
cm.Title = 'Confusion Matrix for Test Data';
cm.ColumnSummary = 'column-normalized';
cm.RowSummary = 'row-normalized';

7.运行结果