1.5 纹理
这次笔记时间有点久,主要是这节课讲的东西需要很多基础来铺垫,看完了后感觉缺失信息很多,又去补了GAMES 101 3~10节内容。 强烈建议看不懂的先去学习GMAES101 网址Lecture 08 Shading 2 (Shading, Pipeline and Texture Mapping)_哔哩哔哩_bilibili
纹理
宏观的角度上来说就是一张2D图片,一个像素上有 RGB 值。
为什么要有纹理
纹理的出现
-
- 减少建模工作量 <=>牺牲几何细节
- 减少存储空间
- 增加读取速度
如果一个模型我们要把所有的细节都表现出来,那无疑是一个巨大工作量,对于简单的模型还好说,但是当我们把工作转换到人体模型上面,人体结构的复杂,外加服装可能各式各样,花式不同,这无疑增大了建模师的工作量。
但是我们如果将一个纹理贴到这些模型上,能保证模拟物体表面的技术没有太大变化,在省略了很多细节之后,也能大致还原原来的表现形式
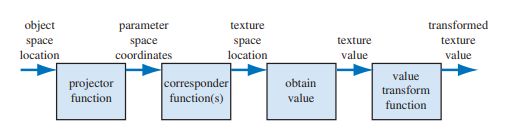
纹理管线
纹理管线是将纹理映射到屏幕像素上的过程。
模型空间位置→投影函数→纹理映射→纹理坐标→通讯函数→新纹理坐标→纹理采样(避免依赖纹理读取)→纹理值。
投影函数:这里与摄像机投影不同,这里是指展UV的技术
依赖纹理读取:也就是只要不是顶点着色器传过来的纹理采样数据,在片元着色器需要计算 UV 偏移,哪怕只是进行了一些计算,也会严重影响性能表现,所以我们需要把 UV 偏移等这些计算放在顶点着色器中计算
纹理采样设置
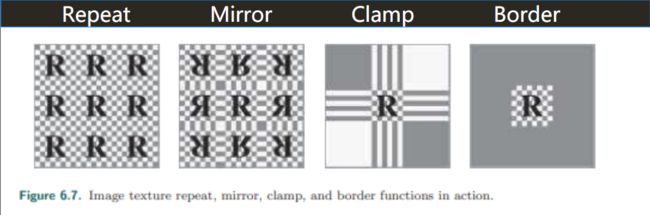
Wrap Mode
决定 UV 值在[0,1]以外的表现
OpenGL -- "包装模式"(Wrapping Model)
DirectX -- "纹理寻址模式"(Texture Addressing Mode)
Repeat —— 重复
Mirror —— 镜像
Clamp —— 这个图形的边界
Border —— 当超过这个范围的其他位置的颜色需要设置
Filter Model
过滤设置,当纹理通过变化产生拉伸的时候,要使用哪种滤波来进行纹理的表现。
-------后续参考GAMES 101 09---------
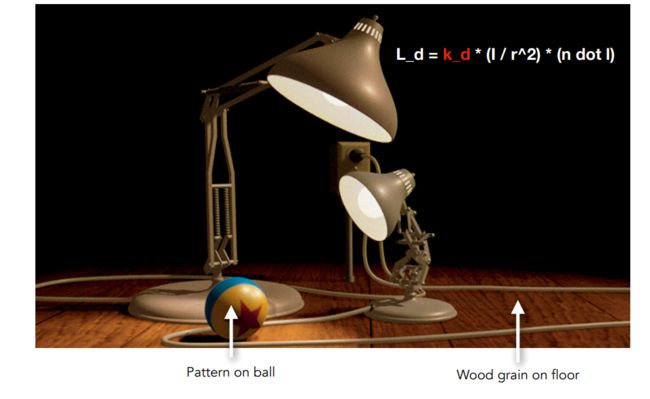
为何有纹理
假设有两个光源打到球上,这个球上面有不同的颜色,也就是说kd的值不同,我们希望能用一种方式来定义这个球上的每一个顶点的属性(纹理坐标、颜色、法线向量等等)。
因此引入纹理。
纹理
纹理可以理解为时覆盖在物体表面的一层布,布上面有着图像,将布放平则得到一个2D图片(Texture)。
所以我们可以认为任何物体表面的图像,都可以撕下来,展开成一张2D图片。同时,图片上的每个点也都能对应上物体上的位置。
纹理映射于物体表面
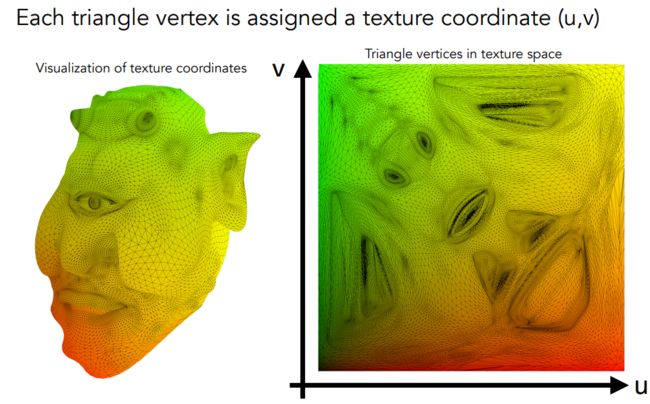
上图所示,空间中的三角面对应纹理中三角形的位置关系
纹理贴图有着自己的纹理坐标,我们一般默认将纹理贴图展开后x轴为u,y轴为v,(在纹理坐标中越往u方向默认颜色为红色,v方向默认为绿色)。
纹理贴图也是我们经常提到的uv图。
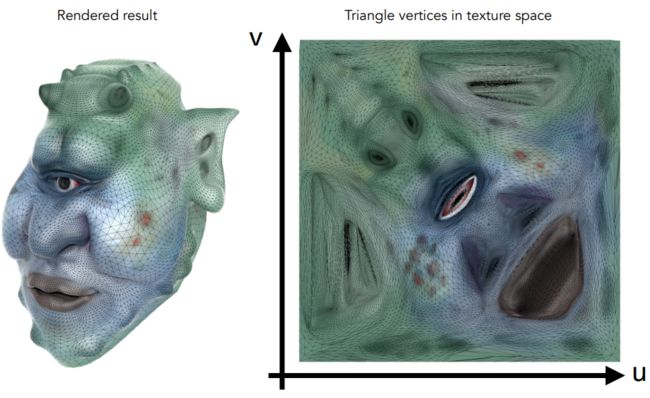
正常uv图展示
渲染好的场景
显示UV坐标下的场景
纹理采样
可以理解为将纹理上的点对应上空间中每一个点。
重心坐标
当由于模型都是由三角面构成,而我们开始拿到的数据是顶点数据,这时我们需要对三角形内部进行插值运算让每个点都平滑过渡,从而得到好的画面效果。
如何进行平滑过渡,则需要用到重心坐标。
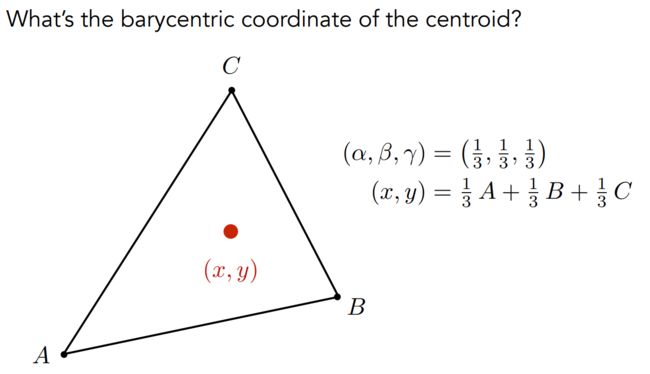
假设点(x,y)是△ABC的重心坐标,则有:
-
- (x,y) = αA+βB+γC
- α+β+γ = 1 结论:限制重心点在ABC所在平面内(为何等于1,因为解释起来复杂,视频未解释)
- (x,y)点在三角形内部,即(α>0 β>0 γ>0)或者(α<0 β<0 γ<0)。
同时满足上面三个条件,则认为(x,y)为△ABC的重心坐标。
由上图可知,AA、AB、AC三角形的面积,分别比上大三角形ABC的面积,得到的比值分别为 α、β、γ 。
(此处α、β、γ为何与第一个特性的α、β、γ对应上,可以参考下方链接有详细的证明步骤)
由此可得,图右公式
根据前两个特性,可得如图所示公式。
最终可得V点坐标,又如开头所说,顶点可以代表任意属性,位置、纹理坐标、颜色、法线、深度、材质等等。
更具体的重心坐标算法可以参考:重心坐标(Barycentric coordinates) - 知乎
但是要注意,这时候三角形已经投影到屏幕上了,尤其对于在三维空间中的属性(比如深度信息),应该找到像素中心点对应三角形的位置的三维空间坐标,然后在三维空间中将A、B、C的深度(属性)插值好,再放回来。这个过程需要做一次逆变换就可以了。
由于空间中的任意三角形顶点都是已知的,上面又可以求出三角形内部的重心坐标。因此我们可以通过差值求出世界空间中三角形内任意一点,然后就可以通过纹理坐标(UV坐标)查询到对应纹理的UV值,这样就可以拿来用了(例如最开始提到的Kd)。
采样方式
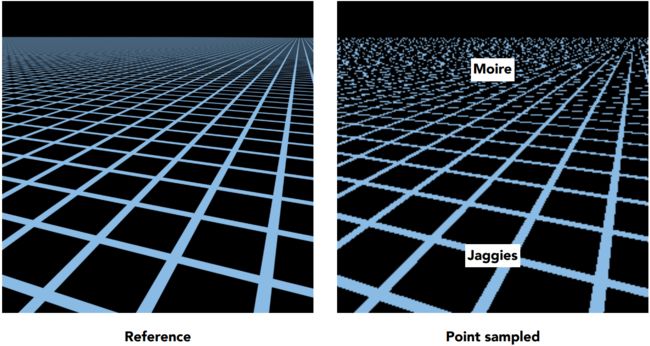
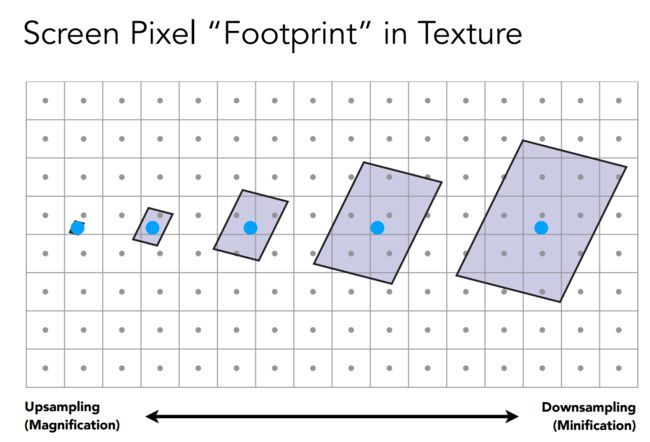
当一张图片的大小小于屏幕像素时,就会发生图片的拉伸,导致图片模糊。
纹理上的纹素、纹理元素(texel)无法一一对应上屏幕上的像素,像素个数>纹素个数,导致在采样时形成类似于马赛克的块状区域。如下图所示。
为应对上述问题,采用以下方法
临近点采样(Nearest)
顾名思义,直接采样里当前像素对应uv坐标中最近的纹素。
优点:速度非常快。
缺点:当纹素个数<像素个数时会产生方块,类似马赛克效果。
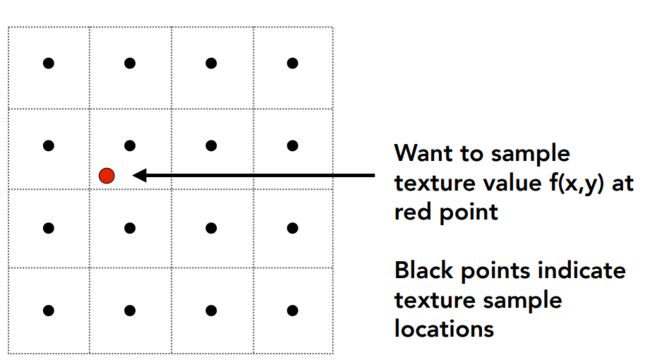
双线性差值(Bilinear Interpolation)
红点为像素,黑点黑框代表纹理。
目的:球红点处对应的纹理属性。
选取当前红点周围四个纹素区域。
此时得到u0(u01与u11的差值),u1(u00与u10的差值)。
再计算u0与u1的差值来得到最终红点的数值,即周围四个区域的差值。
每一个像素点都依次求值最终得到的数值就是Blinear后的结果。
优点:速度快
缺点:最终采样略有瑕疵。
Bicubic
相较于双线性插值算法采样周围四个点,Bicubic则是采样周围16个点。
优点:得到的图片效果相比于前两个最佳。
缺点:相比于前两个速度最慢。
问题与优化
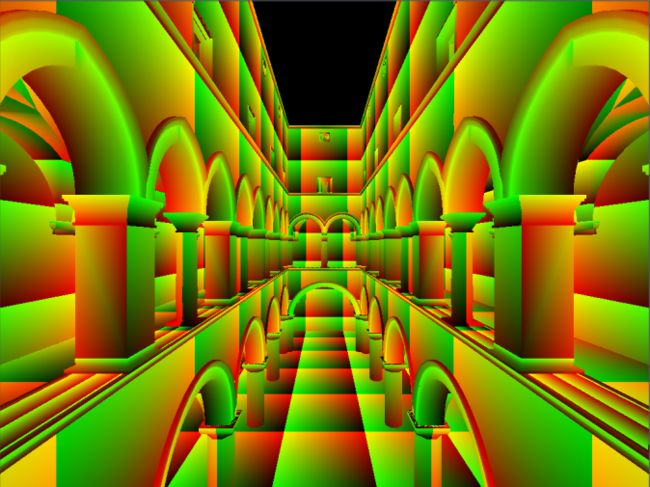
摩尔纹
当一张纹理大小过大大于屏幕像素时就会出现摩尔纹。
原因是因为远处的图像变小,导致一个像素会覆盖对应uv图中一个大的区域,如果按照点采样的话,周围覆盖的纹素信息就会丢失,导致画面信息缺失,出现摩尔纹的情况。
一个简单粗暴的办法就是进行超采样处理,譬如上图右边进行512次的采样,这样就会一定程度上保证画面完整性。
优点:画面最好。
缺点:消耗过大,无法在手机上使用,PC上消耗也很大。
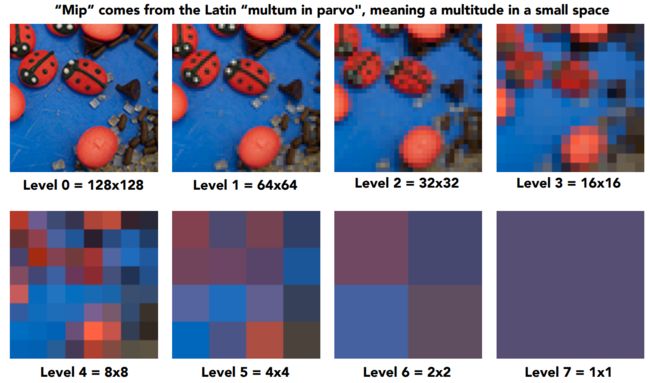
Mipmap
Mipmap的范围查询三个特点:快(查询速度非常快)、大约(是查询的近似值)、方形(查询区域仅可以是方形)。
Mipmap就是将原图片进行等比缩放,每次缩放为原来的2的n次幂,如上图所示。
最终得到的Mipmap图,比原图多了1/3大小。
先要算出当前像素所用的Mipmap等级(D),就要计算出当前区域内像素对应uv坐标里的数值,然后根据计算得到的数值,来选择使用哪个等级的Mipmap。
一个三角形中两个相邻的像素点预估覆盖的区域,在UV坐标中分别对应的点,如上图所示。
以红色的像素点为例,计算出相邻两个像素点在对应UV坐标下的距离L。式子中的dx应该是采用了微分的思想算的。
求得的L当做当前纹理上的长度,又因为默认长度为1(单位长度),所以采取D的等级是
如果这个正方形区域就是1×1,那么就表明一个像素正好对应一个边长为L的正方形区域,也就可以直接在最 原始(第0层,D=0)的纹理上找对应的像素,就是它的值。
如歌这个正方形区域是2×2,那么这个区域会在第1层(D=1)上对应一个像素
如果这个正方形区域是4×4,那么这个区域会在第2层(D=2)上对应一个像素
对于L×L大小的正方形,一定会在D=log2L层上对应到一个像素。
因此我们只需要算出D,即在第几层正方形的区域对应一个像素,就可以得出这个区域内平均值是多少。
将这个分层的过程可视化,如上图所示。
但是会发现,两层之间有很明显的边界,那么在实际纹理映射的过程中可能会出现一些缝。
在此处我们的解决方法是,先找D层,再找D+1层,这两层内部分别用双线性插值把对应的在这两层上的查询做出来,做出来之后把这两个双线性插值的值合到一起,然后在层与层之间再做一次插值。总共做了三步插值,在双线性插值上又加了一步插值,这就是三线性插值。这样我就可以在任意层,无论是整数层还是浮点数层(例如第1.8层,D=1.8)。
各向异性(Anisotropic Filtering)
三线性插值后得到的结果,相较于超采样出来图像,发现在远处的图像全都重叠在了一起。这是因为三线性插值是按照一个方格一个方格来计算的,当碰到斜着的纹理时就无法很好处理这种情况。
![]()
这时就需要用到另一种方式来处理纹理——各向异性(Anisotropic Filtering)
这种方式生成的图片考虑到了图片斜着的情况,即对角线图片,如上图所示。同时图片的大小是原来图片的3倍。
EWA Filtering
人们发明了另外一些方法,如EWA,对于任何一个形状,都可以拆成很多不同的圆形去覆盖这个形状。如上图查询一个椭圆,将其拆成三个圆形,每次去查询一个圆形,多次查询自然就可以得到一个区域,但是代价是“多次查询”。可见质量越高的效果,性能开销越大。
环境贴图
将环境信息放到贴图上,然后采样到物体上得到物体在场景中的环境信息。
球形环境贴图。
球形贴图的问题
将球形贴图展开来看图片的上方和下方都有明显的扭曲。
CubeMap
如何解决球形贴图的问题。
将球想象它在一个立方体内,然后将球表面的纹理信息映射到立方体表面,这样就得到了cubemap。
CubeMap展开后的样子。
法线贴图
用来模拟物体顶点位置的法线。
p为原本顶点位置,n为经过法线贴图变换的p点的位置,此时p点的法线和n点的法线已经不同。
2D空间中,求n点法线。
我们认为,某点p原来的法线n为(0, 1) ,我们要求出改变后的法线,首先就要求出切线,设切向量为(x,y)
由于点p内存储着这一点的高度信息,因此会改变p点的高度,为h(p),利用微分的思想,我们再去找相邻像素点的位置,即p+1处,也有一个高度h(p+1),通过这两点的高度差,就可以算出切向量的y值,即为dp,x的值就是相邻两个像素的x,为1,因此切向量即为(1,dp),所以法向量就是(-dp,1),即法线为(-dp,1)。
3D空间下求得的法线为
![]()
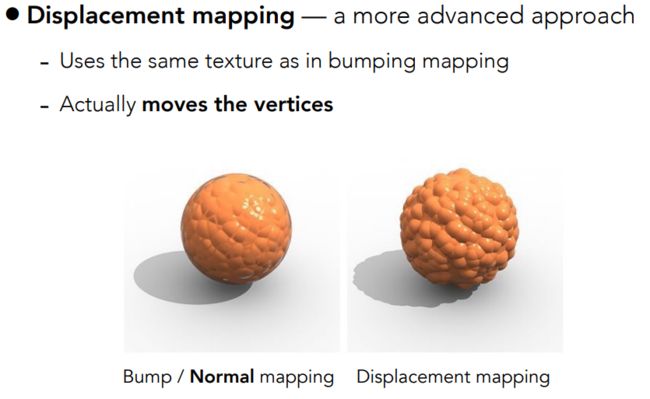
位移贴图(置换贴图)
法线贴图只是模拟物体表面顶点的法线方向,而位移贴图则是实际的改变了物体表面顶点的位置。
噪声图
还可以定义三维纹理,如果把这个球砍一半,可以看到其内部的纹理,这里实际定义了空间中任何一点的值,这种纹理实际没有真的生成纹理的图片,而是定义了一个在三维空间中的噪声函数,对于空间中任意一点都有一个解析式可以算出在该点的值。
环境光遮蔽图、AO图(Ambient Occlusion)
模拟模型被光照后自身所产生的的阴影效果。
3D Textures and Volume Rendering
体渲染中,用3D纹理可以存储物体的密度等。