AdaBoost的求解流程

对于任意Boosting算法，都需要明确以下几点：

        ① 损失函数(,)的表达式是什么？损失函数如何影响模型构建？

        ② 弱评估器()是什么，当下boosting算法使用的具体建树过程是什么？

        ③ 综合集成结果()是什么？集成算法具体如何输出集成结果？

同时，还可能存在其他需要明确的问题，例如：

        ① 是加权求和吗？如果是，加权求和中的权重如何求解？

        ② 训练过程中，拟合的数据与分别是什么？

        ③ 模型训练到什么时候停下来最好？

同时，别忘记boosting算法的基本规则：

        依据上一个弱评估器的结果，计算损失函数，
        并使用自适应地影响下一个弱评估器的构建。
        集成模型输出的结果，受到整体所有弱评估器 ~ 的影响。

在此基本指导思想下，下面将梳理回归算法的基本流程：

AdaBoost.R2

        AdaBoost.R2算法是当前AdaBoost实现流程中使用最多的回归类实践方式，它囊括了对数据进行有放回抽样、按损失函数结果调整样本权重、自动计算弱分类器权重、并输出预测结果等。AdaBoost算法经典的全流程。假设现有数据集N，含有样本个，任意样本编号为，同时，弱评估器为决策树，总共学习轮，则AdaBoost.R2的基本流程如下所示：

① 初始化原始数据集的权重，其中任意

② 在现有数据集中，有放回抽样个样本，构成训练集。在每次抽取一个样本时，任意样本被抽中的概率为，很显然，该概率就是当前样本在训练集中的权重。当从初始权重中抽样时，概率，当后续权重变化时，拥有更大权重的样本被抽中的概率会更大。

③ 在训练集上按照CART树规则建立一棵回归树，训练时所拟合的标签为样本的真实标签

④ 将上所有的样本输入进行预测，得出预测结果，其中i = 1,2,...M。

⑤ 计算单一样本上的损失函数，计算过程如下所示：

        ◉ 求解

        ◉ 选择线性/平方或指数损失函数中的一种计算 ：(线性损失、平方损失、指数损失)

        ◉ 根据AdaBoost的要求，所以损失的值域都在[0,1]之间。

⑥ 计算全样本上的加权平均损失

        注意此时就等于样本的权重。由于，所以一定位于[0,1]范围内，并且一定为1。
        当权重之和为1时，加权平均值一定会小于等于单一数值的最大值（同时大于等于单一数值的最小值），因此加权平均的值域不会超出单一平均数的值域。由于所有损失的值域都是[0,1]，因此加权平均值的值域也是[0,1]。同时，由于损失的最大值为1，而权重的最大值一定是远远小于1的，因此加权平均值的最大值一般也是远远小于1的。

⑦ 依据加权平均损失计算衡量当前集成算法的置信度

，其中是为了防止分母为零的常数。

        不难发现，当加权平平均损失很高时，很大，因此置信度小，当加权平均损失很低时，很小，因此置信度大。置信度越大，集成算法当前的预测结果越好。已知的理论值域是[0,1]，因此的理论值域是[0,+∞]，因此的值越接近0越好。同时，我们还知道的实际范围大约都在0.2~0.3之间，因此一般来说的实际范围基本都是小于1的。

import numpy as np
import matplotlib.pyplot as plt
M = 1000
lambda_ = 1e-6
lt = np.sort(np.random.rand(M))
beta = lt/(1-lt+lambda_)
plt.plot(lt,beta)
plt.ylim(0,5)
plt.vlines(0.5,0,1,linestyles="dotted",color="red")
plt.hlines(1,0,0.5,linestyles="dotted",color="red")
plt.xlabel("lt",fontdict={"fontsize":14})
plt.ylabel("beta",fontdict={"fontsize":14});

 

⑧ 依据置信度评估更新样本权重

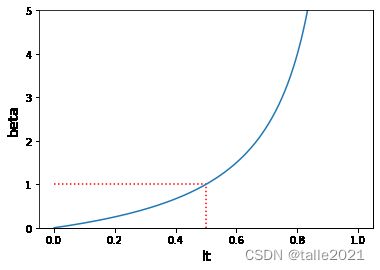
        根据的范围[0,1]，以及的计算公式，绘制出横坐标为，纵坐标为的图像。不难发现，单一样本的损失越大、也会越大，因此该样本的权重会被更新得越大。

import numpy as np
import matplotlib.pyplot as plt
#假设1000个样本
M = 1000
lambda_ = 1e-6

#1000个样本的损失位于[0,1]之间
l = np.linspace(0,0.8,M)

#1000个样本被抽到的概率加和为1
p = np.random.dirichlet(np.ones(M),size=1)
#p = 1/M

#计算加权平均值与beta
lbar = (l*p).sum()
beta = lbar/(1-lbar+lambda_)

l = np.sort(l,axis=0) #从小到大进行排序

#按照1000个样本的l对beta**(1-l)进行绘图
plt.plot(l,beta**(1-l))
plt.xlabel("L_i",fontdict={"fontsize":14})
plt.ylabel("beta^(1-l)",fontdict={"fontsize":14});
print(lbar, beta)

0.3902868424714614 0.6401144497832878

⑨ 求解迭代过程中弱分类器所需的权重

其中log的底数为e或者为2皆可。当值越接近于0，说明损失越小、置信度越高，则的值越大。所以，损失更小的树对应的权重更大，损失更大的树对应的权重更小。

⑩ 求解出当前迭代下集成算法的输出值：

在步骤2~10中循环，直到迭代次数被使用完毕。理想上来说，Adaboost至少应该迭代到次以满足下列条件：

等同于：

并且，最终算法的输出值是上述等式满足“等于”条件时所对应的。对于一个正常迭代的AdaBoost来说，每一轮迭代后获得的都是累加结果，因此之间应该满足以下关系：

在到过程中，必然只有部分是小于真实标签的，假设有次迭代中都小于，则理想状况下，前次迭代中权重的累加，应该大于0.5 * 所有次迭代中权重的累加。当两者相等时，t就是最佳迭代次数，而对应的也就是最佳预测值。

        要完全使用公式来证明以上式子非常困难，但我们可以通过一个简单的小实验来验证该公式的合理性。

ps：原则上应该使用fx计算损失，并且在迭代过程中逐渐计算出权重，但由于计算过程略为复杂，因此在这里简化，直接使用Hx计算损失、beta和权重。这种方法得出的曲线不是最严谨的，但其趋势与使用fx严谨计算的曲线趋势一致，因为原则上来说，只要一个样本被AdaBoost分类正确，这个样本上的损失应该也是越来越小的。

yi = 20
lambda_ = 1e-6
Hx = np.linspace(1,25,1000,endpoint=False) #逐渐增大的Hx

D = np.max(abs(Hx - yi))
L = abs(Hx - yi)/D
beta = L/(1-L+lambda_)

part1 = 0 #用来计算每一轮迭代后的累加值
part1_ = [] #用来保存每一轮迭代后的累加值
part2 = 0
part2_ = []
for t, beta_t in enumerate(beta):
    phi = np.log(1/beta_t)
    #如果Hx小于真实标签yi，则取倒数取对数后放入part1内
    if Hx[t] <= yi:
        part1 += phi
        part1_.append(part1)
    #所有beta取倒数取对数 * 0.5后都放入part2内
    part2 += 0.5*phi
    part2_.append(part2)
plt.plot(range(len(part1_)),part1_,c="red",label = "h < y t")
plt.plot(range(1000),part2_,c="blue",label = "all t")
plt.legend();

#最佳输出值
Hx[len(part1_)-1]

19.984

最终得到的结果为19.984，和最初设置的20非常接近。在AdaBoost回归方法当中，损失函数并没有明显的被“最小化”的过程，而是借助损失函数来自然地调整数据的权重，从而在迭代中不断减小整体损失。