AtcoderABC229场

A - First GridA - First Grid

题目大意

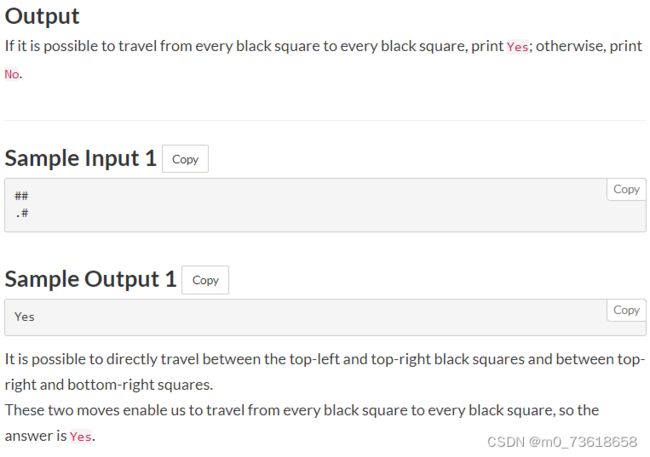
要求判断是否可以从每个黑色方块到达其他所有黑色方块，只能经过黑色方块，并且黑色方块之间必须相连（共享一条边）。

思路分析

据题意，不能的只有以下两种情况

.#  #.
#.  .#

时间复杂度

O(1)

AC代码

#include
using namespace std;
int main(){
  string s1,s2;
  cin >> s1 >> s2;
  if(s1=="#." && s2==".#"){cout << "No\n";}
  else if(s1==".#" && s2=="#."){cout << "No\n";}
  else{cout << "Yes\n";}
  return 0;
}

B - Hard CalculationB - Hard Calculation

题目大意

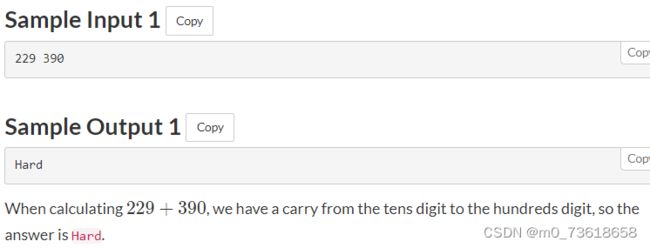
题目要求计算两个给定的正整数 A 和 B 的和，并判断是否有进位。如果没有进位，则输出"Easy"；如果有进位，则输出"Hard"。

思路分析

可以从低位到高位逐位相加，判断每一位的和是否大于等于10。如果大于等于10，则表示有进位，输出"Hard"；否则，继续计算下一位。

时间复杂度

O(log10(A) + log10(B))

AC代码

#include 
using namespace std;

int main() {
    long long A, B;
    cin >> A >> B;
    
    while (A > 0 && B > 0) {
        if ((A % 10) + (B % 10) >= 10) { // 判断当前位的和是否大于等于10
            cout << "Hard" << endl;
            return 0;
        }
        
        A /= 10; // 将数字移动到下一位
        B /= 10;
    }
    
    cout << "Easy" << endl;
    
    return 0;
}

C - Cheese C - Cheese

题目大意

给定了N种奶酪，每种奶酪的美味度和可用数量。需要制作一份美味的奶酪披萨，但披萨上最多只能放W克奶酪。我们需要找到让披萨美味度最大的组合。

思路分析

理论上，按照每克奶酪的美味度从高到低的顺序使用奶酪是最优的。
按照每克奶酪的美味度从高到低对奶酪进行排序。然后，依次选择奶酪，直到披萨上的奶酪总重量达到或超过W克。对于每种美味度高的奶酪，选择尽可能多的使用它，但不能超过它的可用数量。通过累加每种奶酪的美味度乘以使用的重量，就可以得到披萨的最大美味度。

时间复杂度

O(NlogN)

AC代码

#include
using namespace std;
using ll=long long;

int main()
{
  ll n,w;
  cin>>n>>w;
  vector<pair<ll,ll>>v(n);
  
  for(auto &nx:v)
  {
    cin>>nx.first>>nx.second;
  }
  sort(v.begin(),v.end());
  reverse(v.begin(),v.end());
  
  ll res=0; 
  for(auto &nx:v)
  {
    // 使用尽可能多的奶酪，但不能超过可用数量
    ll use=min(w,nx.second);
    res+=nx.first*use;
    w-=use;
  }
  cout<<res<<endl;
  return 0;
}