Outer Product-based Neural Collaborative Filtering
目录
-
-
- 1 Introduction
- 2 Proposed Methods
-
- 2.1 ONCF
- 2.2 ConvNCF
- 3 Experiments
-
- 3.1 模型表现对比
- 3.2 外积和CNN是否有效
- 3.3 超参的影响
-
核心思想： 用外积来构造嵌入维度之间的pair交互。使用多层CNN来提取交互映射间的高阶交互
1 Introduction
设计CF模型的关键:
- 怎样表示用户和物品
- 怎样基于表示构造他们的交互
指出MF的局限性——使用内积：设想嵌入维度之间是独立的；每个维度对预测结果贡献相同。NCF使用多层MLP代替内积来解决这个局限，有一些模型使用用户和物品嵌入concat+多层MLP，元素对应位置相乘等。本文指出这样的设计也很少对嵌入维度间的交互进行建模。虽然MLP可以理论上可以拟合各种连续函数，但是实际情况下，维度间的交互通常很难被MLP学到。
本文使用外积构造嵌入维度之间的交互，这样的交互映射包含丰富的语义信息，能够帮助后续的非线性函数学习嵌入维度间高阶的交互。
2 Proposed Methods
提出了ONCF框架，并且实现了一个具体化实例，ConvNCF
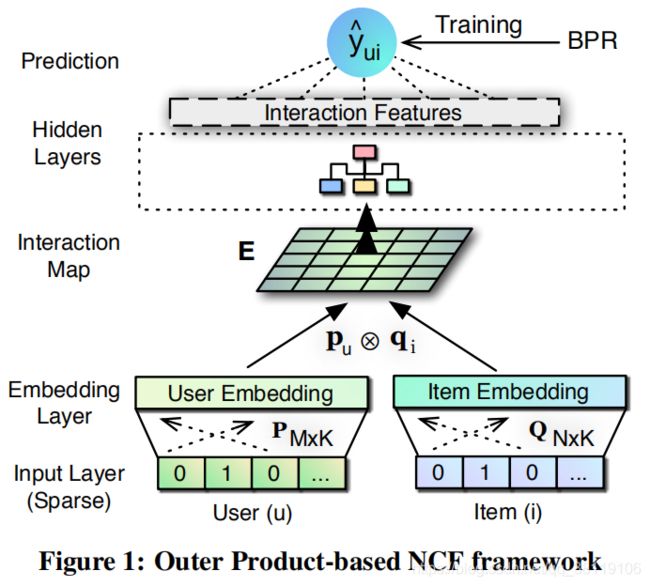
2.1 ONCF
输入和嵌入
按照本文给的嵌入计算方式，不同field的特征嵌入直接相加得到最终的嵌入，所以嵌入是K维。而不是每个field的嵌入concat，得到field数×K的嵌入？？
K，嵌入维度；M，用户特征数量；N，物品特征数量。
交互map
得到K×K的交互map——E。使用外积的好处：
- 包含矩阵分解（只看对角元素）
- 考虑不同嵌入维度之间的相关性，比MF编码了更多信号
- 比concat更有意义，concat保留了嵌入的原始信息，而没有建模任何相关性
[He and Chua, 2017;Beutel et al., 2018]文献表明，对于深度模型适应稀疏数据的问题，显式地对特征嵌入间的交互进行建模很有效，适用concat是次优的。由于E是2D矩阵，可以看做image，就可以使用CV中的先进方法。
隐藏层
目的是从交互映射中提取有用的信号
f 可以是以矩阵为输入，向量为输出的任何函数
预测层
向量为输入，输出预测分
参数空间为 P , Q , θ , w P,Q ,\theta, w P,Q,θ,w，分别为两个嵌入；隐藏层 f 的参数；预测层的参数。
采用BPR损失函数：
对于所有的训练样本对，增大 w w w 都可以扩大 y ^ p o s − y ^ n e g \hat y_{pos}-\hat y_{neg} y^pos−y^neg ，因此对 w w w进行L2正则化。
2.2 ConvNCF
隐藏层可以选择MLP，将矩阵E flat成 K 2 K^2 K2 的输入向量，但是MLP需要太多的参数。采用CNN，需要更少的参数，可以比MLP更容易得建造更深的模型。
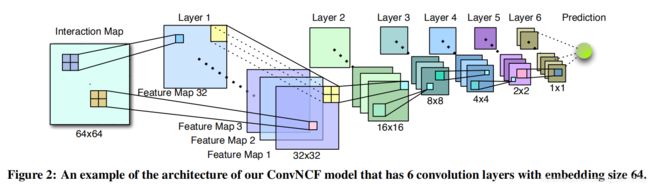
每一层都有32个feature map（可以说卷积核的个数是32 或者说channel数是32），共6层卷积，步长为2，（卷积核应该是2×2，步长2）每一层得到的结果形状是上一层的一半。
- 64×64 32×32×32 16×16×32 8×8×32 4×4×32 2×2×32 1×1×32
- 看作 32维 加预测层 进行预测
那么这6层的卷积参数一共2w多（第一层2×2×32，后面5层，2×2×32×32；128+4096×5=20608），而一层MLP需要800w（4096×2048 ）.
E中每个元素 e i , j e_{i,j} ei,j 表示i和j维度的二阶交互（用元素相乘表示），每一层卷积都捕获了上一层2×2区域的交互。第一层卷积后的结果 e x , y , c 1 e^1_{x,y,c} ex,y,c1，作用于上一层的 [ e 2 x , 2 y , e 2 x , 2 y + 1 , e 2 x + 1 , 2 y , e 2 x + 1 , 2 y + 1 ] [e_{2x,2y},e_{2x,2y+1},e_{2x+1,2y},e_{2x+1,2y+1}] [e2x,2y,e2x,2y+1,e2x+1,2y,e2x+1,2y+1] ，意味着第一层的卷积结果 e x , y , c 1 e^1_{x,y,c} ex,y,c1 捕获了 上一层 [ 2 x , 2 x + 1 , 2 y , 2 y + 1 ] [2x,2x+1,2y,2y+1] [2x,2x+1,2y,2y+1] 区域的4阶交互。那么隐藏层 l l l 中的元素相当于对 E 的 2 l ; 2 l 2^l;2^l 2l;2l 的区域进行高阶交互；最后一层相当于对 64×64 进行编码，对所有维度间交互进行捕捉。通过这种叠加多个卷积层的方法，我们允许ConvNCF从局部到全局学习嵌入维数之间的高阶相关性。
相当于第一层卷积作用于E的2×2，第二层作用于E的4×4（作用于上一层结果的2×2 而上一层作用于E的2×2 所以相当于作用于E 的 2 l × 2 l 2^l×2^l 2l×2l ），第三层作用于E的8×8区域，…，第六层作用于E的64×64。
使用MF得到的嵌入初始化嵌入，训练ConvNCF第一个epoch不加正则化（因为卷积核的参数都是随机初始化，模型现在处于欠拟合状态），从第2个epoch开始加正则化。
3 Experiments
每位用户最新的交互物品作为测试正样本，将其和999个负样本（随机在未交互物品中选出）进行pair。每种模型对于每个用户进行这1000个物品的得分预测，来看真正正样本的得分所rank的位置。使用HR和NDCG评估。
3.1 模型表现对比
- MLP是concat用户和物品嵌入，然后多层MLP
- JRL是用户和物品嵌入对应元素相乘，然后多层MLP
JRL优于MLP，这表明，显式地建模嵌入维数的相关性对于学习后续的隐藏层是有帮助的，即使对于假设维数相互独立的简单相关性也是如此。
3.2 外积和CNN是否有效
外积的对比：使用concat，使用元素对应相乘（GMF就一层直接得预测，JRL加多层MLP得预测）
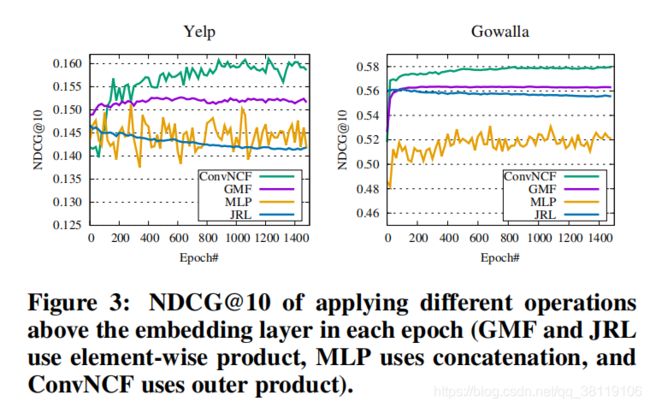
证明了外积得有效，MLP在稀疏数据上不容易学习到。
将多层CNN用3层塔形MLP代替，对比：
3.3 超参的影响
feature map的数量不会导致模型的过拟合问题，证明ConvNCF模型的泛化能力。