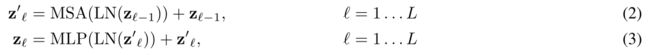TRANSFORMERS FOR IMAGE RECOGNITION AT SCALE—Vision Transformer（ViT）论文详解

论文题目：AN IMAGE IS WORTH 16X16 WORDS：TRANSFORMERS FOR IMAGE RECOGNITION AT SCALE（一张图像值16x16个单词：用于大规模图像识别的Transformer）

期刊合集：最近五年，包含顶刊，顶会，学报>>网址
文章来源：ICLR 2021
代码地址：GitHub

研究背景

 虽然 Transformer 已成为自然语言处理（NLP）的首选模型，但它在计算机视觉方面的应用仍然很少。在计算机视觉任务中，注意力要么与卷积网络结合应用，要么用于替换卷积网络的某些组件，同时保持其整体结构。这种对 CNN 的依赖是不必要的，直接应用于 图像补丁序列的纯 Transformer 可以很好地执行图像分类任务。

问题引入

 受Transformer 在 NLP 任务中成功实践的启发，作者尝试将标准 Transformer 直接应用于图像，并进行最少的修改（不改变整体结构，只修改一些参数），便于可以在开源代码上直接修改使用。

论文分析

 在这篇文章中，作者主要拿 ResNet、ViT（纯Transformer模型）以及 Hybrid（卷积和 Transformer 混合模型）三个模型进行比较。

网络模型

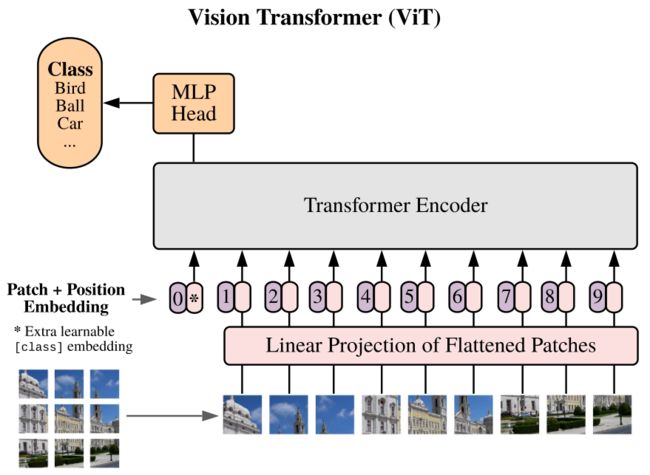
简单来说，VIT 模型由以下三部分组成：

• Linear Projection of Flattened Patches（Embedding 层）
• Transformer Encoder（图右侧结构）
• MLP Head（最终用于分类的层结构）
  

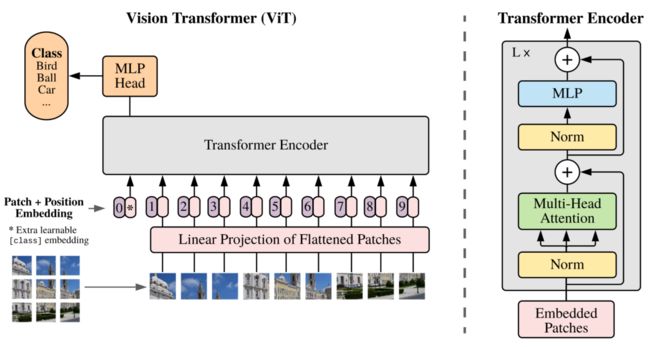
 大致流程：首先将图像分割为固定大小的补丁，线性嵌入每个补丁，添加位置嵌入（position embeddings），为了进行分类，向序列中添加一个额外的可学习的 “分类令牌”（learning embedding），将得到的总和向量序列馈送到标准 Transformer Encoder 中。

1、VISION TRANSFORMER (VIT)

 为处理二维图像，作者首先将图像 x ∈ R ^{H×W ×C} reshape 成一个平面二维 patchs 序列：x_p ∈ R ^N×(p2·C)，其中 ( H, W ) 为原始图像的大小，C 为通道数，( P, P ) 为每个图像斑块的大小，N = HW / p ² 为得到的 patch 数量，作为有效输入序列长度。Transformer 在所有层中使用恒定的潜在向量大小为 D，所以用一个可训练的线性投影( 公式 1 ) 将补丁扁平化并映射到 D 维。作者将这个投影的输出称为补丁嵌入。

 与 BERT 的 [class] 令牌类似，在嵌入的补丁序列 ( z₀⁰ = x_class ) 前会添加一个可学习嵌入，其在 Transformer 编码器 ( z₀^L ) 输出处的状态作为图像表示 y (公式 4)。在预训练和微调期间，分类头附加到 z₀^L 。分类头在预训练时由一个隐含层的 MLP 实现，在微调时由一个线性层实现。

 位置嵌入添加到补丁嵌入中以保留位置信息。文章使用标准的可学习的 1D 位置嵌入，因为没有找到使用更先进的 2D 感知位置嵌入有显著的性能提升，得到的嵌入向量序列作为 Encoder 的输入。

 Transformer encoder 由多头自注意 ( MSA 和 MLP 块交替层组成。在每个块之前应用 Layernorm (LN)，在每个块之后应用残差连接，MLP 包含两个具有 GELU 非线性的层。

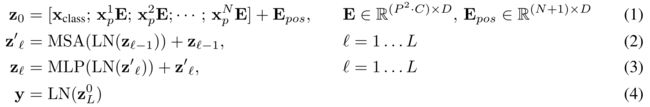
Inductive bias：
 注意到 Vision Transformer 比 cnn 具有更少的图像特定的感应偏差。在 cnn 中，局部性、二维邻域结构和平移等效方差贯穿整个模型的每一层。在 ViT 中，只有 MLP 层是局部的、平移等变的，而自我注意层是全局的。二维邻域结构的使用非常谨慎：在模型开始时，通过将图像切割成块，并在微调时调整不同分辨率图像的位置嵌入(如下所述)。除此之外，初始化时的位置嵌入不包含补丁的二维位置信息，并且必须从头学习补丁之间的所有空间关系。

Hybrid Architecture：
 作为原始图像补丁的替代方案，输入序列可以从CNN的特征图中形成(LeCun et al, 1989)。在这个混合模型中，斑块嵌入投影E (Eq. 1)应用于从CNN特征图中提取的斑块。作为一种特殊情况，patch的空间大小可以为1x1，这意味着输入序列是通过简单地将特征图的空间维度扁平化并投影到Transformer维度来获得的。

如上所述，增加了分类输入嵌入和位置嵌入。

2、FINE-TUNING AND HIGHER RESOLUTION（微调和更高的分辨率）

通常，我们在大型数据集上预训练ViT，并对(较小的)下游任务进行微调。为此，我们去掉预训练的预测头，并附加一个零初始化的D × K前馈层，其中K是下游类的数量。与训练前相比，以更高的分辨率进行微调通常是有益的(Touvron等人，2019;科列斯尼科夫等人，2020)。当输入高分辨率的图像时，我们保持补丁大小相同，这导致更大的有效序列长度。视觉转换器可以处理任意长度的序列(直到内存限制)，然而，预先训练的位置嵌入可能不再有意义。因此，我们根据预训练的位置嵌入在原始图像中的位置执行2D插值。请注意，分辨率调整和补丁提取是关于图像2D结构的感应偏差手动注入Vision Transformer的唯一点。

各个部件详解

VIT 模型由以下三部分组成：

• Linear Projection of Flattened Patches（Embedding 层）
• Transformer Encoder
• MLP Head（最终用于分类的层结构）

1、Embedding 层

 对于一个标准的 Transformer 模块，它要求输入的是 token（向量）序列，即一个二维矩阵 [num_token, token_dim]。如下图，token 0-9 对应的都是向量。

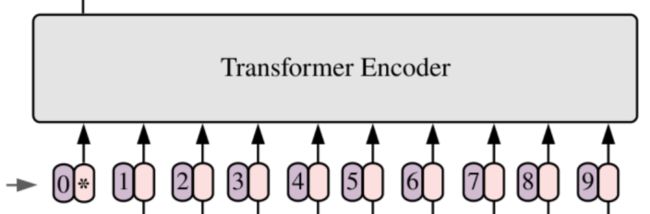
 因为图像的数据格式一般为 [H, W, C] ，它是一个三维矩阵，明显不是 Transformer 想要的，所以需要先通过一个Embedding 层来对数据做个处理。如下图所示，首先将一张图片按给定大小分成一堆 Patches。

 以 ViT-B/16 为例，将输入图片( 224 x 224 ) 按照 16 x 16 大小的 Patch 进行划分，划分后会得到 ( 224 / 16 ) ² = 196 个 Patches。然后通过线性映射（Linear Projection of Flattened Patches）将每个 Patch 映射到一维(1D)向量中，以 ViT-B/16 为例，每个 Patche 数据 shape 为 [16, 16, 3]，通过映射得到一个长度为 768 的向量（后面都直接称为token）。[16, 16, 3] -> [768]

在代码实现中，直接通过一个卷积层来实现。 以ViT-B/16为例，直接使用一个卷积核大小为 16 x 16，步距为16，卷积核个数为 768 的卷积来实现。通过卷积 [224, 224, 3] -> [14, 14, 768]，然后把 H 以及 W 两个维度展平即可 [14, 14, 768] -> [196, 768]，此时变成了一个二维矩阵，正是 Transformer 想要的。

在输入 Transformer Encoder 之前注意需要加上 [class]token 以及 Position Embedding。 作者说参考的是BERT，在得到的一堆 tokens 中插入一个专门用于分类的 [class]token，这个 [class]token 是一个可训练的参数，数据格式和其他 token 一样，都是一个向量，以 ViT-B/16 为例，就是一个长度为 768 的向量，与之前从图片中生成的 tokens 拼接在一起，Cat([1, 768], [196, 768]) -> [197, 768]。这里的 Position Embedding 采用的是一个可训练的参数，是直接叠加在 tokens 上的，所以 shape 要一样。以 ViT-B/16 为例，刚刚拼接 [class]token 后shape 是 [197, 768]，那么这里的 Position Embedding 的 shape 也是 [197, 768]。

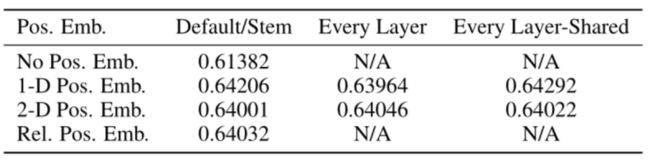
 对于 Position Embedding，作者也有做一系列对比试验，默认使用的是1D Pos. Emb.，对比不使用 Position Embedding 准确率提升了大概 3 个点，和 2D Pos. Emb.比起来没太大差别。

2、Transformer Encoder详解

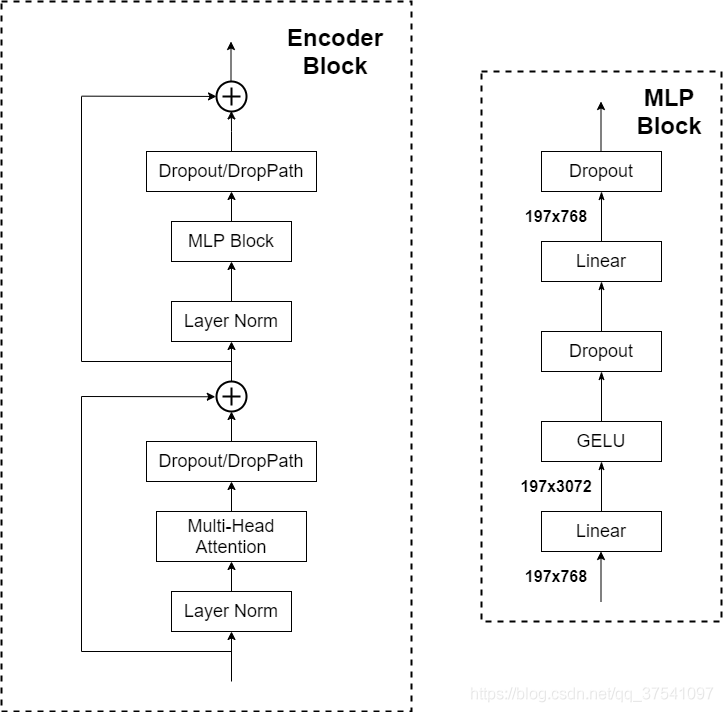
 Transformer Encoder 其实就是重复堆叠 Encoder Block 到 L 次，主要由以下几部分组成：

• Layer Norm，这种 Normalization 方法主要是针对 NLP 领域提出的，这里是对每个 token 进行 Norm 处理，之前也有讲过 Layer Norm 不懂的可以参考链接
• Multi-Head Attention，这个结构之前在讲Transformer中很详细的讲过，不在赘述，不了解的可以参考链接
• Dropout/DropPath，在原论文的代码中是直接使用的Dropout层，在但 rwightman 实现的代码中使用的是DropPath（stochastic depth），可能后者会更好一点。
• MLP Block，如图右侧所示，就是 全连接+GELU激活函数+Dropout 组成也非常简单，需要注意的是第一个全连接层会把输入节点个数翻4倍[197, 768] -> [197, 3072]，第二个全连接层会还原回原节点个数[197, 3072] -> [197, 768]。

3、MLP Head详解

 上面通过 Transformer Encoder 后输出的 shape 和输入的 shape 是保持不变的，以ViT-B/16为例，输入的是[197, 768]输出的还是[197, 768]。但注意的是，在 Transformer Encoder 后其实还有一个 Layer Norm 没有画出来，后面有我自己画的ViT的模型可以看到详细结构。这里我们只是需要分类的信息，所以我们只需要提取出 [class]token 生成的对应结果就行，即[197, 768]中抽取出 [class]token 对应的[1, 768]。接着我们通过 MLP Head 得到我们最终的分类结果。MLP Head 原论文中说在训练 ImageNet21K 时是由 Linear+tanh激活函数+Linear 组成。但是迁移到 ImageNet1K 上或者你自己的数据上时，只用一个 Linear 即可。

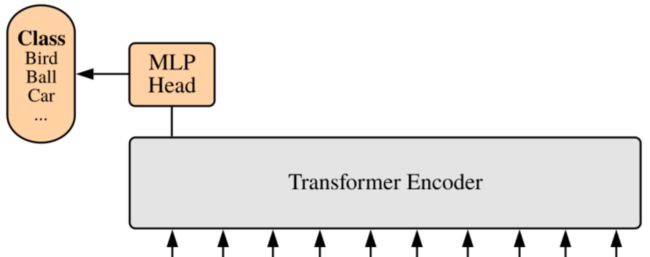
自己绘制的Vision Transformer网络结构
为了方便大家理解，我自己根据源代码画了张更详细的图(以ViT-B/16为例)：

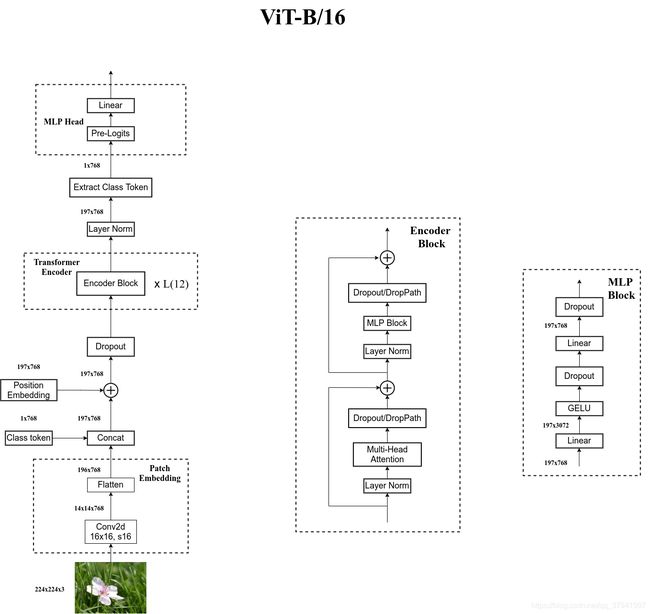
Hybrid模型详解

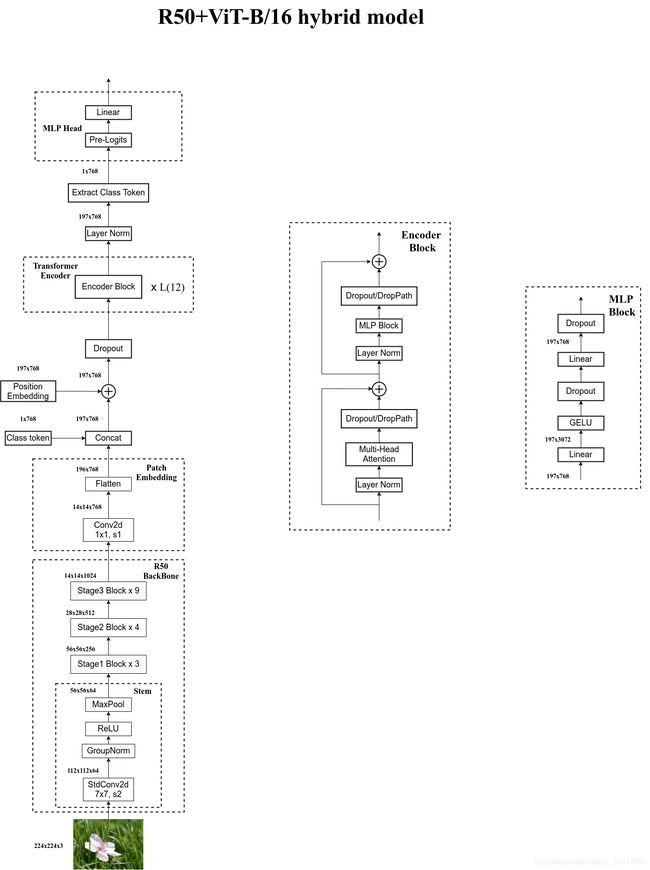
在论文4.1章节的Model Variants中有比较详细的讲到Hybrid混合模型，就是将传统CNN特征提取和Transformer进行结合。下图绘制的是以ResNet50作为特征提取器的混合模型，但这里的Resnet与之前讲的Resnet有些不同。首先这里的R50的卷积层采用的StdConv2d不是传统的Conv2d，然后将所有的BatchNorm层替换成GroupNorm层。在原Resnet50网络中，stage1重复堆叠3次，stage2重复堆叠4次，stage3重复堆叠6次，stage4重复堆叠3次，但在这里的R50中，把stage4中的3个Block移至stage3中，所以stage3中共重复堆叠9次。

通过R50 Backbone进行特征提取后，得到的特征矩阵shape是[14, 14, 1024]，接着再输入Patch Embedding层，注意Patch Embedding中卷积层Conv2d的kernel_size和stride都变成了1，只是用来调整channel。后面的部分和前面ViT中讲的完全一样，就不在赘述。

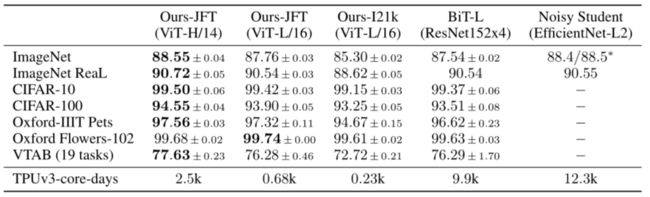
 下表是论文用来对比 ViT，Resnet（使用的卷积层和 Norm 层都进行了修改）以及 Hybrid模型的效果。通过对比发现，在训练 epoch 较少时 Hybrid 优于 ViT，但当 epoch 增大后 ViT 优于 Hybrid。

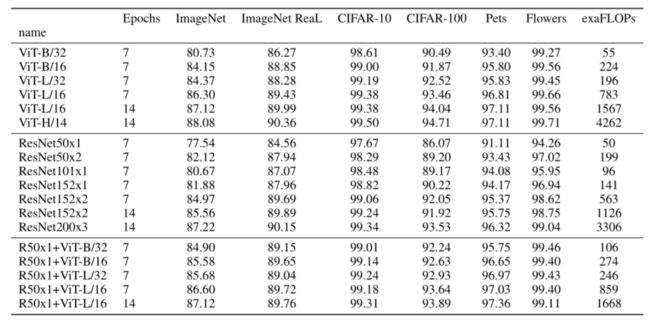
不同类型的 ViT 模型搭建参数

 本篇论文给出三个模型（VIT- Base/ Large/ Huge）的参数，在源码中除了有 Patch Size 为16x16 之外，还有 32x32 的Patch Size。其中的 Layers 就是 Transformer Encoder 中重复堆叠 Encoder Block 的次数，Hidden Size 就是对应通过 Embedding层后每个 token 的 dim（向量的长度），MLP size 是 Transformer Encoder 中 MLP Block 第一个全连接的节点个数（是 Hidden Size 的四倍），Heads 代表 Transformer 中 Multi-Head Attention 的 heads 数，Params 指的是参数规模（M 代表的是百万，而不是MB）。

实验结果

Pytorch 实现

Transformer Encoder 架构图

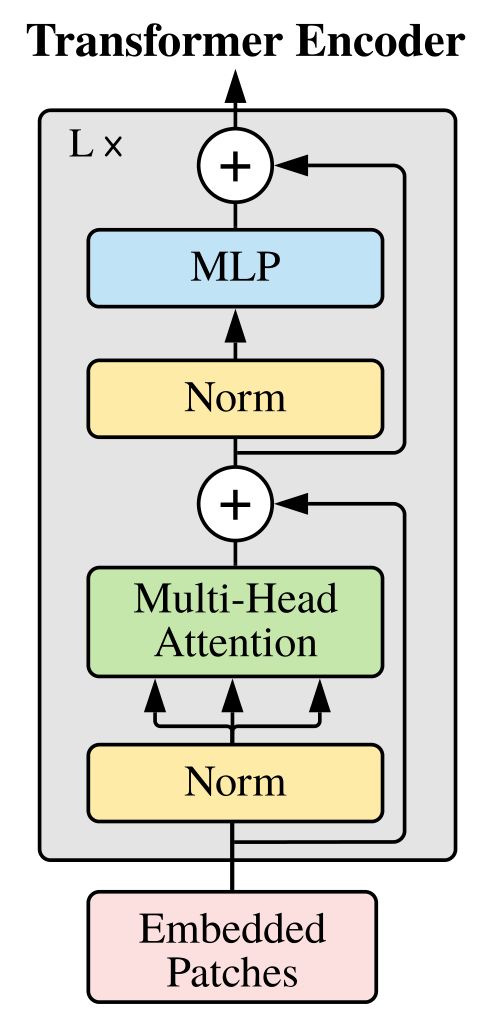
Vision Transformer 架构图

1、包文件

 首先，导入包，其中 einops 和 einsum 包用来操作张量。

import torch
from torch import nn, einsum
import torch.nn.functional as F
from einops import rearrange, repeat
from einops.layers.torch import Rearrange

2、PreNorm 模块

 Layer Norm 层的实现如下，其中参数 dim 是维度，参数 fn 是预先要进行的处理函数，是 Attention 或者 FeedForward，对应以下公式。

class PreNorm(nn.Module):
    def __init__(self, dim, fn):
        super().__init__()
        self.norm = nn.LayerNorm(dim)
        self.fn = fn
    def forward(self, x, **kwargs):
        return self.fn(self.norm(x), **kwargs)

3、FeedForward 模块

 FeedForward 层由线性层，激活函数 GELU 和 Dropout 实现，对应框图中蓝色的 MLP。参数 dim 和 hidden_dim 分别是输入输出的维度和中间层的维度，dropout 则是 dropout 操作的概率参数 p。

class FeedForward(nn.Module):
    def __init__(self, dim, hidden_dim, dropout=0.):
        super().__init__()
        self.net = nn.Sequential(
            nn.Linear(dim, hidden_dim),
            nn.GELU(),
            nn.Dropout(dropout),
            nn.Linear(hidden_dim, dim), 
            nn.Dropout(dropout)
        )
    def forward(self, x):
        return self.net(x)

4、Attention 模块

class Attention(nn.Module):              
    def __init__(self, dim, heads=8, dim_head=64, dropout=0.):
        super().__init__()
        inner_dim = dim_head * heads
        project_out = not (heads == 1 and dim_head == dim)

        self.heads = heads
        self.scale = dim_head ** -0.5

        self.attend = nn.Softmax(dim=-1)
        self.to_qkv = nn.Linear(dim, inner_dim * 3, bias=False)

        self.to_out = nn.Sequential(
            nn.Linear(inner_dim, dim),
            nn.Dropout(dropout),
        ) if project_out else nn.Identity()

    def forward(self, x):
        b, n, _, h = *x.shape, self.heads
        qkv = self.to_qkv(x).chunk(3, dim=-1)      # (b, n(65), dim*3) ---> 3 * (b, n, dim)
        q, k, v = map(lambda t: rearrange(t, 'b n (h d) -> b h n d', h=h), qkv)    # q, k, v   (b, h, n, dim_head(64))

        dots = einsum('b h i d, b h j d -> b h i j', q, k) * self.scale

        attn = self.attend(dots)

        out = einsum('b h i j, b h j d -> b h i d', attn, v)
        out = rearrange(out, 'b h n d -> b n (h d)')
        return self.to_out(out)

 Attention 是 Transformer 中的核心部件，对应框图中的绿色的 Multi-Head Attention。参数 heads 是多头自注意力的头的数目，dim_head 是每个头的维度。

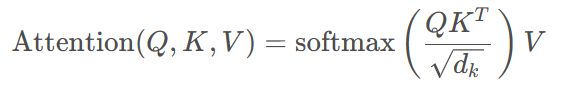
5、Transformer 模块

class Transformer(nn.Module):
    def __init__(self, dim, depth, heads, dim_head, mlp_dim, dropout=0.):
        super().__init__()
        self.layers = nn.ModuleList([])
        for _ in range(depth):
            self.layers.append(nn.ModuleList([
                PreNorm(dim, Attention(dim, heads=heads, dim_head=dim_head, dropout=dropout)),
                PreNorm(dim, FeedForward(dim, mlp_dim, dropout=dropout))
            ]))
    
    def forward(self, x):
        for attn, ff in self.layers:
            x = attn(x) + x
            x = ff(x) + x
        return x

定义好几个层之后，我们就可以构建整个Transformer Block了，即对应框图中的整个右半部分Transformer Encoder。有了前面的铺垫，整个Block的实现看起来非常简洁。

参数depth是每个Transformer Block重复的次数，其他参数与上面各个层的介绍相同。

笔者也在图中也做了标注与代码的各部分对应。

6、ViT 模块

class ViT(nn.Module):
    def __init__(self, *, image_size, patch_size, num_classes, dim, depth, heads, mlp_dim, pool='cls', channels=3, dim_head=64, dropout=0., emb_dropout=0.):
        super().__init__()
        image_height, image_width = pair(image_size)
        patch_height, patch_width = pair(patch_size)

        assert  image_height % patch_height ==0 and image_width % patch_width == 0

        num_patches = (image_height // patch_height) * (image_width // patch_width)
        patch_dim = channels * patch_height * patch_width
        assert pool in {'cls', 'mean'}

        self.to_patch_embedding = nn.Sequential(
            Rearrange('b c (h p1) (w p2) -> b (h w) (p1 p2 c)', p1=patch_height, p2=patch_width),
            nn.Linear(patch_dim, dim)
        )

        self.pos_embedding = nn.Parameter(torch.randn(1, num_patches+1, dim))
        self.cls_token = nn.Parameter(torch.randn(1, 1, dim))					# nn.Parameter()定义可学习参数
        self.dropout = nn.Dropout(emb_dropout)

        self.transformer = Transformer(dim, depth, heads, dim_head, mlp_dim, dropout)

        self.pool = pool
        self.to_latent = nn.Identity()

        self.mlp_head = nn.Sequential(
            nn.LayerNorm(dim),
            nn.Linear(dim, num_classes)
        )

    def forward(self, img):
        x = self.to_patch_embedding(img)        # b c (h p1) (w p2) -> b (h w) (p1 p2 c) -> b (h w) dim
        b, n, _ = x.shape           # b表示batchSize, n表示每个块的空间分辨率, _表示一个块内有多少个值

        cls_tokens = repeat(self.cls_token, '() n d -> b n d', b=b)  # self.cls_token: (1, 1, dim) -> cls_tokens: (batchSize, 1, dim)  
        x = torch.cat((cls_tokens, x), dim=1)               # 将cls_token拼接到patch token中去       (b, 65, dim)
        x += self.pos_embedding[:, :(n+1)]                  # 加位置嵌入（直接加）      (b, 65, dim)
        x = self.dropout(x)

        x = self.transformer(x)                                                 # (b, 65, dim)

        x = x.mean(dim=1) if self.pool == 'mean' else x[:, 0]                   # (b, dim)

        x = self.to_latent(x)                                                   # Identity (b, dim)
        print(x.shape)
        return self.mlp_head(x)                                                 #  (b, num_classes)

合并成一个文件

import torch
from torch import nn, einsum
import torch.nn.functional as F
from einops import rearrange, repeat
from einops.layers.torch import Rearrange


# PreNorm模块，生成layerNorm
class PreNorm(nn.Module):
    def __init__(self, dim, fn):
        super().__init__()
        self.norm = nn.LayerNorm(dim)
        self.fn = fn
    def forward(self, x, **kwargs):
        return self.fn(self.norm(x), **kwargs)


# Attention模块
class Attention(nn.Module):              
    def __init__(self, dim, heads=8, dim_head=64, dropout=0.):
        super().__init__()
        inner_dim = dim_head * heads
        project_out = not (heads == 1 and dim_head == dim)

        self.heads = heads
        self.scale = dim_head ** -0.5

        self.attend = nn.Softmax(dim=-1)  # softMax操作
        self.to_qkv = nn.Linear(dim, inner_dim * 3, bias=False)  # 将dim:1024 * 3

        self.to_out = nn.Sequential(
            nn.Linear(inner_dim, dim),
            nn.Dropout(dropout),
        ) if project_out else nn.Identity()

    def forward(self, x):
        b, n, _, h = *x.shape, self.heads 
        qkv = self.to_qkv(x).chunk(3, dim=-1)    # 对tensor张量分块  x:1  197(cls一起的token)  1024(需要映射的维度)  qkv最后是一个元组，长度是3，每个元素形状：1 197 1024
        q, k, v = map(lambda t: rearrange(t, 'b n (h d) -> b h n d', h=h), qkv)    # 分头操作

        dots = einsum('b h i d, b h j d -> b h i j', q, k) * self.scale  # attention那个公式

        attn = self.attend(dots)

        out = einsum('b h i j, b h j d -> b h i d', attn, v)  # 乘以对应的v矩阵
        out = rearrange(out, 'b h n d -> b n (h d)')
        return self.to_out(out)

class FeedForward(nn.Module):
    def __init__(self, dim, hidden_dim, dropout=0.):
        super().__init__()
        self.net = nn.Sequential(
            nn.Linear(dim, hidden_dim),
            nn.GELU(),
            nn.Dropout(dropout),
            nn.Linear(hidden_dim, dim), 
            nn.Dropout(dropout)
        )
    def forward(self, x):
        return self.net(x)


# Transformer模块
class Transformer(nn.Module):
    def __init__(self, dim, depth, heads, dim_head, mlp_dim, dropout=0.):
        super().__init__()
        self.layers = nn.ModuleList([])
        for _ in range(depth):   # Encoder，包含了Attention、FeedForward模块，堆叠在一起
            self.layers.append(nn.ModuleList([
                PreNorm(dim, Attention(dim, heads=heads, dim_head=dim_head, dropout=dropout)),
                PreNorm(dim, FeedForward(dim, mlp_dim, dropout=dropout))
            ]))
    
    def forward(self, x):
        for attn, ff in self.layers:
            x = attn(x) + x
            x = ff(x) + x
        return x



# ViT 模块
class ViT(nn.Module):
    def __init__(self, *, image_size, patch_size, num_classes, dim, depth, heads, mlp_dim, pool='cls', channels=3, dim_head=64, dropout=0., emb_dropout=0.):
        super().__init__()
        image_height, image_width = pair(image_size)  # 输入图片的宽和高：224*224
        patch_height, patch_width = pair(patch_size)  # patch的宽和高：16*16

        assert  image_height % patch_height ==0 and image_width % patch_width == 0

        num_patches = (image_height // patch_height) * (image_width // patch_width)  # 一张图可以分多少个patch
        patch_dim = channels * patch_height * patch_width  # 将整个token作展平操作
        assert pool in {'cls', 'mean'} # 使用cls

        self.to_patch_embedding = nn.Sequential(
            Rearrange('b c (h p1) (w p2) -> b (h w) (p1 p2 c)', p1=patch_height, p2=patch_width),
            nn.Linear(patch_dim, dim)
        )

        self.pos_embedding = nn.Parameter(torch.randn(1, num_patches+1, dim))  # 生成包括cls的所有位置编码
        self.cls_token = nn.Parameter(torch.randn(1, 1, dim))		# nn.Parameter()定义可学习参数
        self.dropout = nn.Dropout(emb_dropout)  # NLP中常规操作

        self.transformer = Transformer(dim, depth, heads, dim_head, mlp_dim, dropout)

        self.pool = pool
        self.to_latent = nn.Identity()

        self.mlp_head = nn.Sequential(
            nn.LayerNorm(dim),
            nn.Linear(dim, num_classes)
        )  # 对cls的操作，做分类任务

    def forward(self, img):
        x = self.to_patch_embedding(img)        # b c (h p1) (w p2) -> b (h w) (p1 p2 c) -> b (h w) dim
        # img 1  3  224  224 --> 输出x：1 196 1024
        b, n, _ = x.shape           # b表示batchSize, n表示每个块的空间分辨率, _表示一个块内有多少个值

        cls_tokens = repeat(self.cls_token, '() n d -> b n d', b=b)  # self.cls_token: (1, 1, dim) -> cls_tokens: (batchSize, 1, dim)  复制batchSize份cls符号
        x = torch.cat((cls_tokens, x), dim=1)               # 将cls_token拼接到patch token中去       (b, 65, dim)
        x += self.pos_embedding[:, :(n+1)]                  # 加位置嵌入（直接加）      (b, 65, dim)
        x = self.dropout(x)

        x = self.transformer(x)               # (b, 65, dim)

        x = x.mean(dim=1) if self.pool == 'mean' else x[:, 0]       # (b, dim)

        x = self.to_latent(x)                                       # Identity (b, dim)
        print(x.shape)
        return self.mlp_head(x)                                    #  (b, num_classes)  多分类任务


# 实例化ViT
v = ViT(
    image_size = 224,
    patch_size = 16,
    num_classes = 1000,  # 作1000个类别
    dim = 1024,
    depth = 6,  # 几个Encoder
    heads = 16，
    mlp_dim = 2048,
    dropout = 0.1,
    emb_dropout = 0.1
)

img = torch.randn(1, 3, 224, 224)

preds = v(img)

print(preds.shape) # (1, 1000)

代码注释都有，有问题的小伙伴，欢迎大家在评论区提问。

参考链接：Vision Transformer 详解
Layer Normalization 解析
Self-Attention以及Multi-Head Attention
Pytorch代码实现参考
B站视频解读