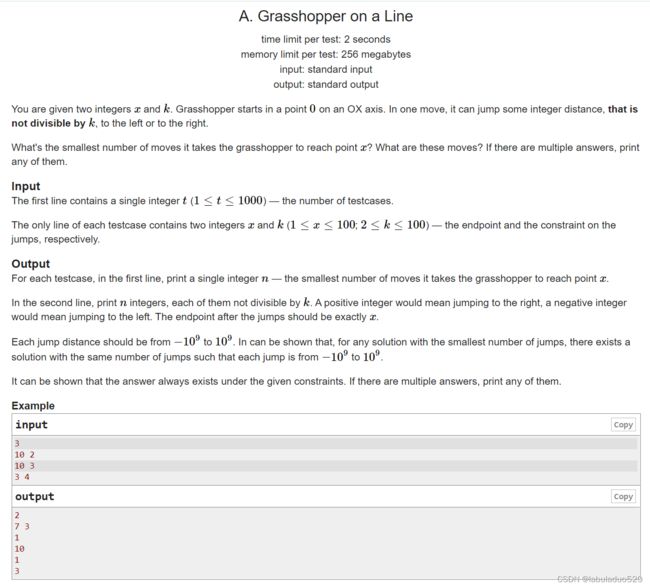
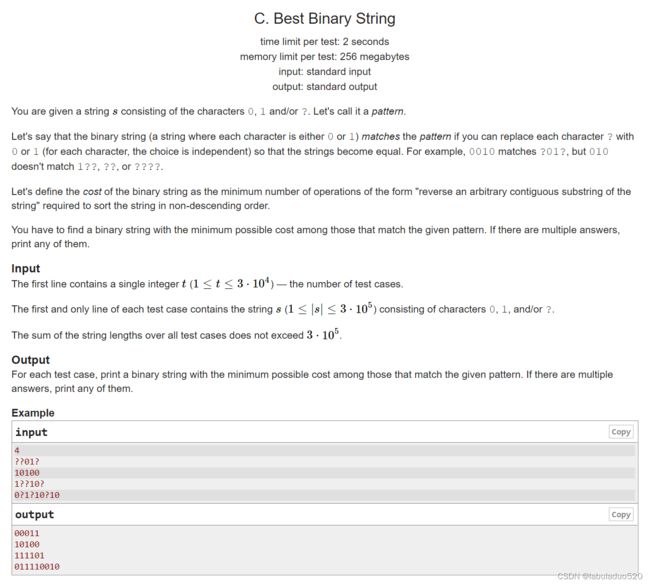
CF1837 A-D
A题
题目链接：https://codeforces.com/problemset/problem/1837/A
基本思路：
要求计算蚂蚱到达位置 x最少需要多少次跳跃，并输出蚂蚱的跳跃方案。因为每次可以向左或向右跳跃一定距离（距离必须为整数），但是不能跳到距离为 k 的整数倍的位置上。又因为
，所以分两种情况讨论。第一种情况：x%k==0，时，先跳x-1的距离，再跳1的距离，最后到达x点。第二种情况：x%k!=0时，可以直接跳到x点。
AC代码：
#include
#include
using namespace std;
typedef long long ll;
typedef long double db;
void solve()
{
int x, k;
cin >> x >> k;
if (x % k == 0)
{
cout << 2 << endl;
cout << x - 1 << " " << 1 << endl;
}
else
{
cout << 1 << endl;
cout << x << endl;
}
}
int main()
{
int t;
cin >> t;
while (t--)
{
solve();
}
return 0;
} B题
题目链接：https://codeforces.com/problemset/problem/1837/B
基本思路：
因为要求出与 字符串s 相容的所有数列中花费最小的数列的花费。所以只需要求出连续子串“<<<......”或“>>>......”的最大的长度，最后再+1即可。
AC代码：
#include
#include
#include
#include
using namespace std;
typedef long long ll;
typedef long double db;
void solve()
{
int n;
cin >> n;
string s;
cin >> s;
int res = 0, maxx = 0;
char op = s[0];
for (int i = 0; i < n; i++)
{
if (op == s[i])
{
res++;
maxx = max(maxx, res);
}
else
{
maxx = max(maxx, res);
res = 1;
op = s[i];
}
}
cout << maxx + 1 << endl;
}
int main()
{
int t;
cin >> t;
while (t--)
{
solve();
}
return 0;
} C题
题目链接：https://codeforces.com/problemset/problem/1837/C
基本思路：
因为构造的字符串要使通过“反转”操作使原字符串成为升序的操作次数尽可能的小。因此我们可以先求出从左到右第一个不是'?'的字符，并用变量op将其保存，之后从左到右依次遍历字符串s，当s[i]=='?'时，用op对其进行赋值，当碰到s[i]!='?'时，将s[i]赋值给变量op，起到更新的作用。最后将字符串s打印输出即可。
AC代码：
#include
#include
#include
#include
using namespace std;
typedef long long ll;
typedef long double db;
void solve()
{
string s;
cin >> s;
char op = '0';
for (int i = 0; i < s.length(); i++)
{
if (s[i] != '?')
{
op = s[i];
break;
}
}
for (int i = 0; i < s.length(); i++)
{
if (s[i] == '?')
{
s[i] = op;
}
else
{
op = s[i];
}
}
cout << s << endl;
}
int main()
{
int t;
cin >> t;
while (t--)
{
solve();
}
return 0;
} D题
题目链接：https://codeforces.com/problemset/problem/1837/D
基本思路：
因为一个括号序列是否优美，必须满足以下两个条件中的任意一个：
1、序列的任意一个前缀中，左括号的个数不少于右括号的个数，且整个序列中，左括号的个数等于右括号的个数。
2、序列的任意一个前缀中，右括号的个数不少于左括号的个数，且整个序列中，左括号的个数等于右括号的个数。
题目要求：给定一个括号序列，你需要把它分成若干组，使得每一组的括号构成的序列都是优美的。求最少需要分成多少组，并输出分组方案。如果无解，输出 −1。
首先，当“(”的数量和“)”的数量不相等时，一定无法构成优美的括号序列。
当能构成优美的括号序列时，因为括号序列是否优美，需要满足上述两个条件中的任意一个，因此最多可以将序列分为2组，一组满足第一种情况，另一组满足第二种情况。
因此，我们只需要从左到右遍历整个序列，op作为临时变量存储第一个出现的括号，以此来表示这个字符应该属于第一种还是第二种。maxx存储该字符属于第几种的数字。cnt代表最少需要分成多少组。res表示当前组是否划分完毕，如果等于0，表示当前序列已经划分到了maxx组中，之后再对后续序列进行判断划分。
AC代码：
#include
#include
#include
#include
using namespace std;
typedef long long ll;
typedef long double db;
void solve()
{
int n, a[200005];
cin >> n;
string s;
cin >> s;
int ans1 = 0, ans2 = 0;
for (int i = 0; i < n; i++)
{
if (s[i] == '(')ans1++;
else ans2++;
}
if (ans1 != ans2)
{
cout << -1 << endl;
}
else
{
int res = 0, maxx = 1, cnt = 0;
char op = s[0];
for (int i = 0; i < n; i++)
{
if (res == 0)
op = s[i];
if (s[i] == op)
{
a[i] = maxx;
cnt = max(cnt, maxx);
res++;
}
else
{
if (res > 0)
{
res--;
a[i] = maxx;
}
if (res == 0 && i + 1 < n && s[i + 1] != op)
{
if (maxx == 1)
{
maxx++;
}
else
{
maxx--;
}
}
}
}
cout << cnt << endl;
for (int i = 0; i < n; i++)
{
cout << a[i] << " ";
}
cout << endl;
}
}
int main()
{
int t;
cin >> t;
while (t--)
{
solve();
}
return 0;
}