Raki的读paper小记：Retentive Network: A Successor to Transformer for Large Language Models

Abstract&Introduction&Related Work

• 研究任务
  语言模型的基础架构
• 已有方法和相关工作
  • S4，H3，Hyena，Linear Transformer
  • 用核函数近似注意力，以便将自回归推理重写为循环形式
  • 回归到使用循环模型进行高效推理，但牺牲了训练并行性。为了弥补这一点，使用元素级操作[PAA+23]进行加速，但同时损害了表示能力和性能
  • 尝试用其他机制取代注意力，例如S4[GGR21]及其变体[DFS+22，PMN+23]
• 面临挑战
• 创新思路
  • RetNet = linear attention + rope + 显式衰减（即 $\gamma$）
• 实验结论
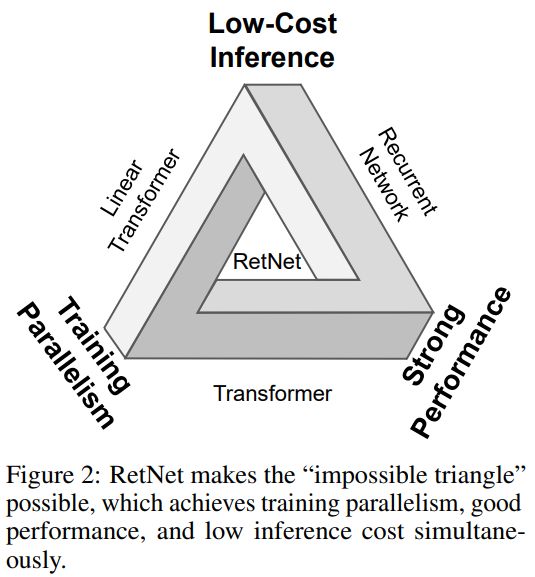
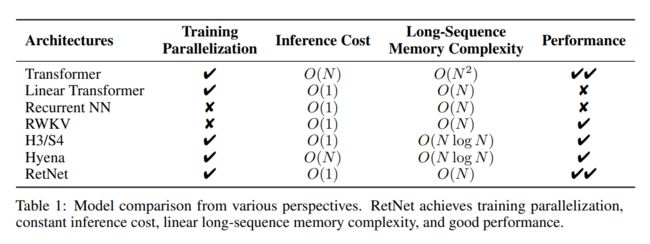
  实现了不可能三角，实现了O(1)推理
  

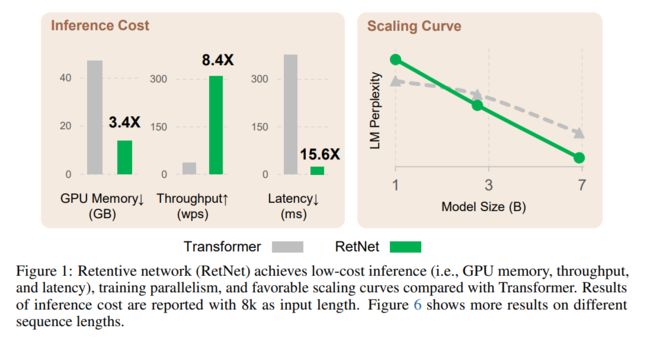
Retentive Networks

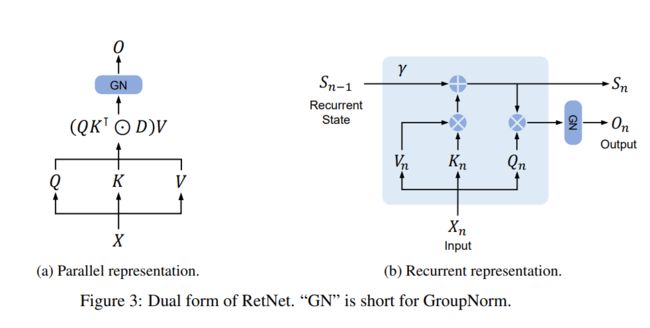
先来看一下Retention跟Attention的区别，首先第一眼感觉retention有点像RNN和LSTM

attention的计算方式是QK做矩阵乘法，使用query和key计算权重分布，对value加权

retention使用了一个线性衰减参数$\gamma$，使用了一个状态向量S

给定输入$X\in {\mathbb{R}}^{|x|\times d_{\mathrm{model}}}$，我们将其投影到一维函数 $v(n)=X_n\cdot w_V$。考虑一个序列建模问题，通过状态 $s_n$ 将 $v(n)$映射为 $o(n)$, 为简单起见，用$v_n、o_n$ 表示 $v(n)$ 和 $o(n)$, 以递归方式形式化映射过程：

$\begin{array}{rlr}{s}_n& =A{s}_{n-1}+K_n^{\mathsf{T}}{v}_n,& A\in {\mathbb{R}}^{d\times d},K_n\in {\mathbb{R}}^{1\times d}\\ o_n& =Q_n{s}_n=\sum _{m=1}^n{Q}_n{A}^{n-m}{K}_m^{\mathsf{T}}{v}_m,& Q_n\in {\mathbb{R}}^{1\times d}\end{array}$

将vn映射到状态向量sn，并通过线性变换来递归地编码序列信息。接下来使投影 $Q_n$、$K_n$变得与内容相关：$Q=X{W}_Q,K=X{W}_K$

将矩阵A对角化$A=\Lambda (\gamma e^{i\theta }){\Lambda }^{-1}$，由$A^{n-m}=\Lambda (\gamma e^{i\theta }{)}^{n-m}{\Lambda }^{-1}$得到$o(n)$改进后的输出表达式：
$\begin{array}{rl}{o}_n& =\sum _{m=1}^n{Q}_n(\gamma e^{i\theta }{)}^{n-m}{K}_m^{⊺}{v}_m\\ & =\sum _{m=1}^n(Q_n(\gamma e^{i\theta }{)}^n)(K_m(\gamma e^{i\theta }{)}^{-m}{)}^{⊺}{v}_m\end{array}$

$Q_n(\gamma e^{i\theta }{)}^n,K_m(\gamma e^{i\theta }{)}^{-m}$ 在xPos中被大家周知，这里使用了类似Transformer中提出的相对位置嵌入。我们进一步将γ简化为一个标量：$o_n={\sum }_{m=1}^n{\gamma }^{n-m}(Q_n{e}^{in\theta })(K_m{e}^{im\theta }{)}^{†}{v}_m$

The Parallel Representation of Retention

最后retention的公式如下：
$$\begin{gathered} Q=(X{W}_Q)\odot \Theta ,K=(X{W}_K)\odot \overline{\Theta },V=X{W}_V \\ {\Theta }_n=e^{in\theta },D_{nm}=\{\begin{array}{cc}{\gamma }^{n-m},& n\ge m\\ 0,& n<m\end{array} \\ \text{Retention}(X)=(Q{K}^{⊺}\odot D)V \end{gathered}$$

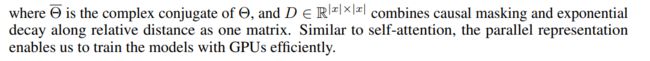
也可以写成循环的方式：
$\begin{array}{l}{S}_n=\gamma S_{n-1}+K_n^{⊺}{V}_n\\ \text{Retention}(X_n)=Q_n{S}_n,n=1,\cdots ,|x|\end{array}$

保持机制的分块循环表示

为了加速训练，特别是对于较长的序列，这里采用了一种并行表示和循环表示的混合形式。将输入序列分成块。在每个块内，采用并行表示进行计算。跨块信息通过循环表示传递。具体来说，设B表示块长度。我们通过以下方式计算第i个块的保持输出：
$\begin{array}{rl}& Q_{[i]}=Q_{Bi:B(i+1)},K_{[i]}=K_{Bi:B(i+1)},V_{[i]}=V_{Bi:B(i+1)}\\ R_i& =K_{[i]}^{⊺}{V}_{[i]}+{\gamma }^B{R}_{i-1}\\ \mathrm{Retention}(X_{[i]})& =\underset{\text{Inner-Chunk}}{(Q_{[i]}{K}_{[i]}^{\mathsf{T}}\odot D)V_{[i]}}+\underset{\text{Cross-Chunk}}{(Q_{[i]}{R}_i)\odot \xi },{\xi }_{ij}={\gamma }^{i+1}\end{array}$

跟attention的示意图对比：

Gated Multi-Scale Retention

在每一层中，我们使用 $h=d_{model}/d$个retention heads，其中d是头的维度。这些头使用不同的参数矩阵 $W_Q、W_K、W_V\in {\mathbb{R}}^{d_{\mathrm{model}}\times d_{\mathrm{model}}}$ 。多尺度保持（MSR）为每个头分配不同的γ。为了简单起见，我们在不同层之间设置相同的γ，并将它们固定。此外，我们添加了一个Swish门[HG16, RZL17]来增加保持层的非线性。具体而言，给定输入X，我们定义该层为：
$\begin{array}{rl}\gamma & =1-2^{-5-\mathrm{arange}(0,h)}\in {\mathbb{R}}^h\\ {\mathrm{head}}_i& =\mathrm{Retention}(X,{\gamma }_i)\\ \mathbf{Y}& =\mathrm{Group}{\text{Norm}}_h(\mathrm{Concat}({\mathrm{head}}_1,\cdots ,{\mathrm{head}}_h))\\ \mathrm{MSR}(X)& =(\mathrm{swish}(X{W}_G)\odot Y)W_O\end{array}$

组归一化（GroupNorm）[WH18]用于对每个头的输出进行归一化，遵循在[SPP+19]中提出的SubLN。请注意，不同的γ尺度会导致不同的方差统计数据。因此，我们分别对头的输出进行归一化。保持机制的伪代码总结在图4中：

归一化：

packed embeddings$X^0=[{\mathbf{x}}_1,\cdots ,{\mathbf{x}}_{|x|}]\in {\mathbb{R}}^{|x|\times d_{\mathrm{model}}}$ 作为模型输入，计算模型输出：

$\begin{array}{rl}{Y}^l& =\mathrm{MSR}(\mathrm{LN}(X^l))+X^l\\ X^{l+1}& =\mathrm{FFN}(\mathrm{LN}(Y^l))+Y^l\end{array}$

LN是layernorm
$FFN(X)=gelu(X{W}_1)W_2$

在训练过程中，我们使用并行和分块循环表示。序列内或块内的并行化有效地利用GPU加速计算。更重要的是，分块循环特别适用于长序列训练，无论是在FLOPs还是内存消耗方面都非常高效

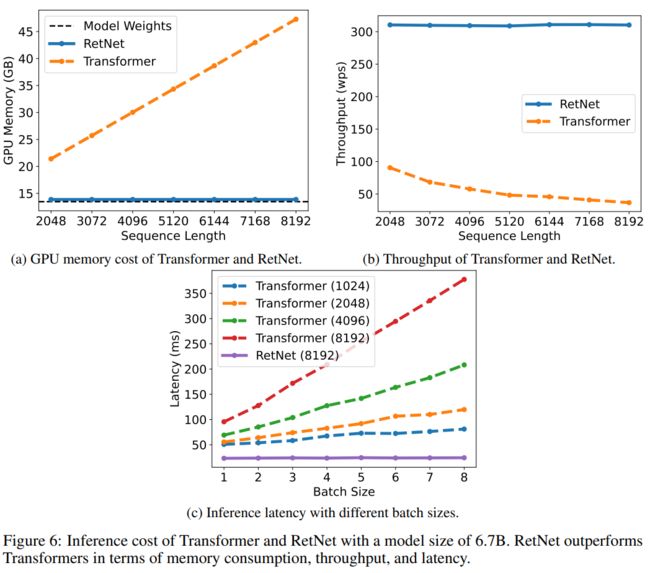
在推理过程中，我们采用循环表示，这非常适合自回归解码。O(1)复杂度降低了内存和推理延迟，同时实现了相同的结果

与其他方法的差异：

Experiments

Conclusions

在本研究中，我们提出了保持网络（RetNet）用于序列建模，实现了多种表示方式，即并行、循环和分块循环。相比Transformer，RetNet在推理效率（内存、速度和延迟方面）、训练并行化和竞争性能方面都取得了显著优势。上述优势使得RetNet成为大型语言模型中理想的Transformer继任者，特别是考虑到O(1)推理复杂度带来的部署优势。未来，我们希望在模型规模[CDH+22]和训练步骤方面扩展RetNet。此外，通过压缩长期记忆，保持机制能够高效地与结构化提示[HSB+22b]结合使用。我们还将使用RetNet作为骨干架构来训练多模式大型语言模型[HSB+22a，HDW+23，PWD+23]。此外，我们对在各种边缘设备上部署RetNet模型，如移动手机等，也充满兴趣。

Remark

用线性注意力+rope位置编码+权重衰减，得到了在小任务上的效率和效果全方面吊打transformer的结果，但是长距离建模能力暂时未知，毕竟transformer的建模是能看到前面所有模块，而retnet是由前一个状态转移得来，有cherry picking可能，不过不管如何，都是一个了不起的工作，如tianxiang哥所说，文本的diffusion时期可能很快就要到来，一举成为取代attention方式decoder的超强方法，甚至于不用regressive方式的解码（but我自己觉得自回归就是我心目中的终极奥义了，至少是终极奥义的组成部分，不可能被完全不使用），期待后续工作推进在长序列上的建模能力，不管如何，在low resource的情况下，retnet这种架构必然会大展身手，毕竟transformer的推理代价过高导致很多情况都是不可能使用（以目前的硬件水平 不过我很相信老黄），嗯 希望成为或者引出下一个划时代的工作