信贷风险控制管理-策略生成及规则挖掘
在信贷风险管理领域,通常有两种主要的风险控制方法,即规则引擎和风险模型。规则引擎使用一组简单的规则进行客户分类,使得不同客户群体的期望风险存在显著差异,并能够快速进行风险划分。而风险模型则使用机器学习技术预测客户的违约风险,尽管精度相对较高,但建模和上线周期较长。因此,在需要快速进行客户划分或者精度要求不高的场景中,一般会采用规则挖掘和规则引擎快速上线的方式。对于精度要求较高的场景,则会采用规则引擎粗筛+模型精选相结合的方式进行风险决策。
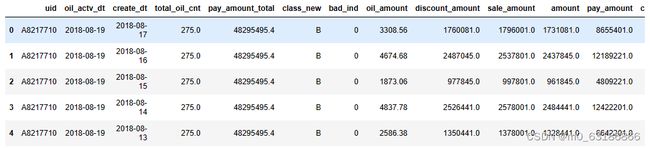
本文以某公司的“油品贷”数据为例,使用决策树算法进行策略制定。
业务背景:某打车平台和某些加油站达成合作,联合推出油品贷业务,可以给打车平台的司机提供贷款等业务,但最近发现使用油品贷的人,坏账率很高,数据高达5%,否则项目会被砍掉。
来申请油品贷的司机本身本身已经通过了评分卡,并分为六个评分等级A-F。公司领导发现只有给等级A的客户放款才能不亏钱,现需要我们在现在的基础上制定有效的规则策略,控制坏账率。
滴滴是和很多加油站有合作的,加油站会给滴滴提供司机数据。
| 变量类型 | 最终基础变量名(还需要做上述变换) | 释义 |
| 数值统计型 | ||
| oil_amount | 加油升数 | |
| discount_amount | 折扣金额 | |
| sale_amount | 促销金额 | |
| amount | 总金额 | |
| pay_amount | 实际支付金额 | |
| coupon_amount | 优惠券金额 | |
| payment_coupon_amount | 支付优惠券金额 | |
| 分类型 | ||
| channel_code | 渠道 | |
| oil_code | 油品品类(规格) | |
| scene | 场景 | |
| source_app | 来源端口(1货车帮、2微信) | |
| call_source | 订单来源(1:中化扫描枪 2:pos 3:找油网 4:油掌柜5:司机自助加油 6 油站线) |
一,首先要导入所需要的库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import tree二,导入所需要的数据
data = pd.read_csv(r"F:\rankingcard.csv",index_col = 0) ##导入数据三,数据预览
3.1 查看数据基本情况
# 查看前5行数据详情
data. Head()数据部分展示:
3.2 查看数据基本情况
# 数据整体描述
data.describe() ![]()
3.3查看数据维度
# 数据维度情况
data.shape数据一共有50609行,19列,其中有18个特征,1列是标签。
3.4粗略查看数据类型、个数、判断缺失值情况
# 数据基本信息
data.info()从这里可以发现数据中某些特征具有缺失值。
3.5 查看缺失值情况
## 缺失值百分比显示
data.isnull().sum()/len(data)# 查看标签正负样本的分布情况
data['bad_ind'].value_counts()## 可视化饼图
data['bad_ind'].value_counts().plot(kind='pie')3.6 查看时间跨度
## 查看样本的时间跨度
data['create_dt'].min(),data['create_dt'].max() ![]()
3.7 查看在时间上的分布
## 样本在时间上的分布情况,以月为单位进行聚合
data.groupby([pd.DatetimeIndex(data['create_dt']).year,pd.DatetimeIndex(data['create_dt']).month]).agg({"create_dt":np.size})四、数据预处理
4.1 根据特征变量类型和加工方式的不同进行划分
## org_lst 不需要做特殊变换,保留原始内容,然后直接去重
## agg_lst 数值型变量做聚合
## dstc_lst 离散型变量做count
org_lst = ['uid','create_dt','oil_actv_dt','class_new','bad_ind']
agg_lst = ['oil_amount','discount_amount','sale_amount','amount','pay_amount','coupon_amount','payment_coupon_amount']
dstc_lst = ['channel_code','oil_code','scene','source_app','call_source']# 拷贝不同类型特征的数据,保留底表
df = data[org_lst].copy()
df[agg_lst] = data[agg_lst].copy()
df[dstc_lst] = data[dstc_lst].copy()4.2 时间缺失值填充
# 按'uid','create_dt'进行逆序排序
df2 = df.sort_values(['uid','create_dt'], ascending = False)## 之间已经看出oil_actv_dt没有缺失值
def time_isna(x, y):
return y if str(x) == 'NaT' else x
# 用oil_actv_dt来对缺失的creat_dt做补全,
df2['create_dt'] = df2.apply(lambda x: time_isna(x.create_dt, x.oil_actv_dt), axis = 1)4.3 样本截取
对creat_dt做补全,用oil_actv_dt来填补,并且截取6个月的数据
构造变量的时候不能直接对历史所有数据做累加。
否则随着时间的推移,变量分布会有很大的变化,否则规则很快就会不适用。
# 截取放款日和创建日期之差在6个月内的数据。
df2['dtn'] = (df2.oil_actv_dt - df2.create_dt).apply(lambda x :x.days)df = df2[df2['dtn'] < 180]
df4.3 重复样本进行去重操作
# 对org_list变量求历史贷款天数的最大间隔,并且去重,保留最新的一条数据
base = df[org_lst]
base['dtn'] = df['dtn']
base = base.sort_values(['uid','create_dt'],ascending = False)
base = base.drop_duplicates(['uid'],keep = 'first')base. Shape ##查看数据维度此时引入一个概念
value = badrate 表示坏账人数除以总人数
(base.loc[:,'bad_ind']==1).sum()/len(base) ##坏账率![]()
可以看出该油品贷的坏账率达到4.66%
五、特征衍生
5.1 特征衍生-连续型变量
做一些基础的求和、行数、最大最小值、均值等等特征衍生操作
# 对连续型变量进行聚合衍生
gn = pd.DataFrame()
for i in agg_lst:
# 统计当前特征值个数
tp = pd.DataFrame(df.groupby('uid').apply(lambda df:len(df[i])).reset_index())
tp.columns = ['uid',i + '_cnt']
if gn.empty == True:
gn = tp
else:
gn = pd.merge(gn,tp,on = 'uid',how = 'left')
# 统计当前特征值大于0的个数
tp = pd.DataFrame(df.groupby('uid').apply(lambda df:np.where(df[i] > 0, 1, 0).sum()).reset_index())
tp.columns = ['uid',i + '_num']
if gn.empty == True:
gn = tp
else:
gn = pd.merge(gn,tp,on = 'uid',how = 'left')
# 对当前特征的历史数据求和
tp = pd.DataFrame(df.groupby('uid').apply(lambda df:np.nansum(df[i])).reset_index())
tp.columns = ['uid',i + '_tot']
if gn.empty == True:
gn = tp
else:
gn = pd.merge(gn,tp,on = 'uid',how = 'left')
# 求当前特征历史数据均值
tp = pd.DataFrame(df.groupby('uid').apply(lambda df:np.nanmean(df[i])).reset_index())
tp.columns = ['uid',i + '_avg']
if gn.empty == True:
gn = tp
else:
gn = pd.merge(gn,tp,on = 'uid',how = 'left')
# 求当前特征历史数据最大值
tp = pd.DataFrame(df.groupby('uid').apply(lambda df:np.nanmax(df[i])).reset_index())
tp.columns = ['uid',i + '_max']
if gn.empty == True:
gn = tp
else:
gn = pd.merge(gn,tp,on = 'uid',how = 'left')
# 求当前特征历史数据最小值
tp = pd.DataFrame(df.groupby('uid').apply(lambda df:np.nanmin(df[i])).reset_index())
tp.columns = ['uid',i + '_min']
if gn.empty == True:
gn = tp
else:
gn = pd.merge(gn,tp,on = 'uid',how = 'left')
# 求当前特征历史数据方差
tp = pd.DataFrame(df.groupby('uid').apply(lambda df:np.nanvar(df[i])).reset_index())
tp.columns = ['uid',i + '_var']
if gn.empty == True:
gn = tp
else:
gn = pd.merge(gn,tp,on = 'uid',how = 'left')
# 求当前特征历史数据极差
tp = pd.DataFrame(df.groupby('uid').apply(lambda df:np.nanmax(df[i]) -np.nanmin(df[i]) ).reset_index())
tp.columns = ['uid',i + '_ran']
if gn.empty == True:
gn = tp
else:
gn = pd.merge(gn,tp,on = 'uid',how = 'left')
# 求当前特征历史数据变异系数,避免除0,使用0.01进行平滑
tp = pd.DataFrame(df.groupby('uid').apply(lambda df:np.nanmean(df[i]) / (np.nanvar(df[i]) + 0.01)).reset_index())
tp.columns = ['uid',i + '_cva']
if gn.empty == True:
gn = tp
else:
gn = pd.merge(gn,tp,on = 'uid',how = 'left')5.2对离散变量进行特征操作
gc = pd.DataFrame()
for i in dstc_lst:
tp = pd.DataFrame(df.groupby('uid').apply(lambda df:len(set(df[i]))).reset_index())
tp.columns = ['uid',i+'_dstc']
if gc.empty == True:
gc = tp
else:
gc = pd.merge(gc,tp,on = 'uid',how = 'left')5.3 将做好的特征衍生放到一个新的DataFrame中,使用表连接方式
fn = pd.merge(base,gn,on = 'uid')
fn = pd.merge(fn,gc,on='uid')
fn = fn.fillna(0)
fn.shape六、训练树模型
# 移除训练集中的无关列
x = fn.drop(['uid','oil_actv_dt','create_dt','bad_ind','class_new'],axis = 1)
# 构建标签列
y = fn.bad_ind
# 采用CART树进行规则挖掘
r_tree = tree.DecisionTreeRegressor(
# r_tree = tree.DecisionTreeClassifier(
max_depth = 3,
min_samples_leaf = 500, min_samples_split=5000)
r_tree = r_tree.fit(x, y)该树的模型当中,设置三个参数,max_depth最大深度为3,min_samples_leaf表示在叶节点处需要的最小样本数为500,min_samples_split表示拆分内部节点所需的最少样本数为5000。
# 使用graphviz进行可视化展示
import graphviz
dot_data = tree.export_graphviz(
r_tree,
out_file = None,
feature_names = x.columns,
class_names = ['good','bad'],
filled=True,
rounded=True,
special_characters=True)
graph = graphviz.Source(dot_data) 这样我们就建好了一棵树,接下来根据生成好的树开始生成策略。
## 生成策略
dff1 = fn.loc[(fn.amount_tot>48077.5)&(fn.coupon_amount_cnt>3.5)].copy()
dff1['level'] = 'oil_A'
dff2 = fn.loc[(fn.amount_tot>48077.5)&(fn.coupon_amount_cnt<=3.5)].copy()
dff2['level'] = 'oil_B'
dff3 = fn.loc[fn.amount_tot<=48077.5].copy()
dff3['level'] = 'oil_C'dff1 = dff1.append(dff2) ##将dff2填入dff1
dff1 = dff1.append(dff3) ##将dff3填入dff1len(dff1) ##查看一下dff1的维度last = dff1[['class_new','level','bad_ind','uid','oil_actv_dt','bad_ind']].copy()
last['oil_actv_dt'] = last['oil_actv_dt'].apply(lambda x:str(x)[:7]).copy() ##截取字符串前7个字符
last. head()last.to_excel(path, index = False) ##将弄好的文件存放到某一个文件夹将保存好的excel打开,使用数据透视表进行数据分析:
最后结果如下所示:结合原始数据中的类别(class_new),对样本进一步细分,选出bad_rate较小的类别,作为可放宽群体。深色部分表示可以放款的。
(1)坏账率分布
| 坏账率分布 | 贷前分类 | |||||||
| A | B | C | D | E | F | 总计 | ||
| 油品分类 | oil_A | 0.9% | 0.7% | 1.6% | 1.7% | 2.9% | 5.5% | 1.2% |
| oil_B | 1.8% | 2.2% | 2.7% | 5.3% | 6.2% | 13.1% | 3.0% | |
| oil_C | 5.1% | 6.7% | 6.3% | 5.9% | 15.2% | 19.9% | 7.4% | |
| 总计 | 2.9% | 3.9% | 4.2% | 4.9% | 10.6% | 16.1% | 4.7% | |
(2)人数分布
| 人数分布 | 贷前分类 | |||||||
| A | B | C | D | E | F | 总计 | ||
| 油品分类 | oil_A | 4.9% | 12.6% | 3.9% | 2.6% | 0.9% | 0.7% | 25.6% |
| oil_B | 5.0% | 12.5% | 4.1% | 3.2% | 0.9% | 0.8% | 26.4% | |
| oil_C | 7.3% | 21.6% | 7.5% | 6.8% | 2.4% | 2.4% | 48.0% | |
| 总计 | 17.1% | 46.7% | 15.5% | 12.6% | 4.3% | 3.8% | 100.0% | |
(3)结果对比 :以前只放贷给评分卡等级为A的用户,现在对深色的都可以放贷,可放贷款人数增加且坏账率降低。
| 可放款人数 | 可放款人数占比 | 坏账率 | |
| 现计划 | 5052 | 45.5% | 1.6% |
| 原计划 | 1901 | 17.1% | 2.9% |