TA入门笔记（十）

参考
may佬《技术美术百人计划》
冯乐乐《UnityShader 入门精要》
【Unity Shaders】法线纹理（Normal Mapping）的实现细节
光照模型 PBR

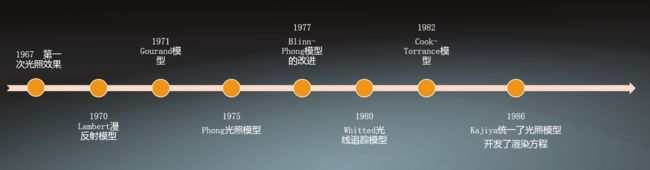
图形2.4 传统经验光照模型详解

光照模型概述

光照模型（illumination model），也称为明暗模型，用于计算物体某点处的光强（颜色）。从算法理论基础而言，光照模型分为两类：一种是基于物理理论的，另一种是基于经验模型的。

基于物理理论的光照模型（PBR）

偏重于使用物理的度量和统计方法，效果非常真实，但是计算复杂，实现起来也较为困难

经验模型

是对光照的一种模拟，通过实践总结出简化的方法，简化了真实的光照计算，并且能达到很不错的效果

现实世界的光照极其复杂，而且会受到诸多因素的影响，有限的计算能力无法完全模拟。使用简化的光照模型对现实的情况进行近似，使得计算处理起来会更容易，并且使效果更符合需求。

光照模型发展的时间轴：

局部光照模型

只考虑来自光源的直接光照影响，不考虑来自其他物体反射的间接光
局部光照模型满足叠加原理，可以基本将光线分为四个部分：漫反射、高光反射、环境光、自发光

漫反射

• 当光线从光源照射到模型表面时，光线被均匀反射到各个方向，这种现象就是漫反射
• 漫反射过程中，光线发生了吸收（改变颜色）和散射（改变方向）
• 使用lambert余弦定理来计算漫反射光照

Lambert余弦定理

简单的说，反射光线的强度与表面法线和光源方向之间的夹角的余弦成正比

公式：$$color=C_{light}\ast albedo\ast dot(normal,L)$$

• $C_{light}$：入射光颜色
• $albedo$：模型漫反射材质
• 漫反射效果与观察者位置无关，与光源位置有关
• 兰伯特模型无法提供高光效果，制作出来的材质偏向橡胶

镜面反射（高光反射）

公式：$$C_{specular}=C_{light}\ast m_{specular}\ast saturate(dot(v,r){)}^{m_{gloss}}$$
$$r=l-2\ast dot(n,l)\ast n$$

• $m_{gloss}$表示了材质的光泽度，$m_{specular}$表示材质的反射光

• r表示反射光 推导

• v表示视线向量

• 光泽度越大，高光范围越小，衰减越快
  
  

环境光

在局部光照模型中，由于没有考虑间接光照的影响，因此为了处理这种间接光照为光照模型引入环境光
公式：$$C_{ambient}=Albedo\ast Ambien{t}_{light}$$

• 通常使用漫反射的反照率来指示环境光照的反射光量，假定场景中多次发生散射和反射，并在所有方向上均等的射向目标物体

自发光

物体自身发射的光线，通常作为单独的一项加入光照模型，用一张发光贴图描述物体的自发光

经典光照模型

Lambert模型（兰伯特）

基于Lambert余弦定理，完整公式即为漫反射公式

• 半兰伯特：将映射范围从-1 ~ 1变为0 ~ 1

只有固有色，没有高光

Phong模型

Phong模型是第一个有影响力的光照模型，考虑直接光照的反射作用，使用环境光代替间接光照

• $A_{light}$：环境光量
• $C_{light}$：入射光量
• $m_{diffuse}$：漫反射率
• $m_{specular}$：镜面反射率
• $l$：指向光源入射光向量
• $n$：物体表面法线
• $r$：反射向量
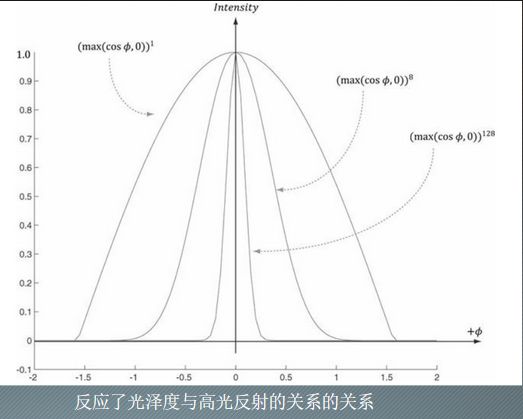
• $gloss$：光泽度，用于控制高光反射区域

相比于lambert模型，出现了高光，整体亮度提高

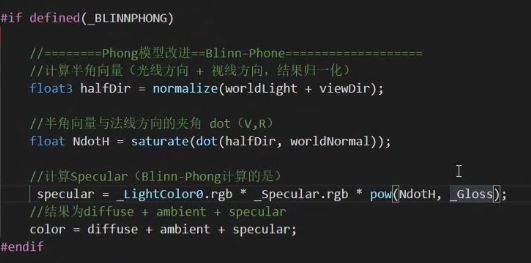
Blinn-Phong模型

Blinn-Phong模型不再依赖于反射向量，而是采用了所谓的半程向量（Halfway Vector），即光线与视线夹角一半方向上的一个单位向量。当半程向量与法线向量越接近时，镜面光分量就越大



相比于Phong模型高光部分会更大一些

使用半角向量带来的变化

• 计算更加简洁，半角向量比反射向量易得
• 当光源与视线都在物体表面上时，半角向量与法线的角度永远不大于90度
  
  

Flat模型

平面着色模型，计算多边形的单个强度，每个三角形只有一个法线方向。以相同的光强度显示多边形的所有点。通常适用于lowPoly风格的场景

总结

• Lambert模型只考虑表面的漫反射
• Phong模型能够较好地呈现镜面高光的效果，也是四种模型中最接近真实效果的，需要计算较复杂的反射向量
• Blinn-Phong模型效果与Phong模型相近，更偏向艺术性的效果，使用方便计算的半程向量代替较为复杂的反射向量，计算量小于Phong，是效果和效率的最佳选择，也是大多数情况下的默认光照模型

作业·拓展

法线贴图

法线纹理存储的是切线空间（tangent space）中的顶点法线方向。

• 切线空间中，顶点位置为坐标原点，法线本身方向为z轴（normal），取和纹理坐标方向相同的一条切线为x轴（tangent），再做叉乘即可得到切线空间的坐标系（bi-tangent）。
• 法线方向不变时，在切线空间中的normal就是z轴方向，即（0，0，1）。因为向量每个维度的取值范围是（-1，1），而纹理每个通道的范围是（0，1），因此需要进行一次映射pixel=(normal+1)/2,于是切线空间的法线值（0，0，1）对应了法线纹理中的RGB值（0.5，0.5，1），这就是法线纹理主要为蓝色的原因

在unity shader中对法线纹理采样需要使用UnpackNormal函数，即将法线纹理的颜色值重新映射回正确的法线方向

        // Lookup the normal from the normal map
        vec4 normal = texture( NormalMapTex, TexCoord );
        normal.xyz = normal.xyz * 2 - 1;

通过转换矩阵可以将获得的切线空间下的法线方向转换到世界空间

//计算法线切线副法线副切线
        o.normalDir = UnityObjectToWorldNormal(v.normal);
        o.tangentDir = normalize(mul(unity_ObjectToWorld,float4(v.tangent.xyz,0.0)).xyz);
        o.bitangentDir = normalize(cross(o.normalDir,o.tangentDir) * v.tangent.w);

		//Normal
        i.normalDir = worldNormal;
        float3x3 tangentTransform = float3x3(i.tangentDir,i.bitangentDir,i.normalDir);

        //获取映射过的法线贴图,准备最终法线
        float3 normalLocal = UnpackNormal(tex2D(_Normalmap,TRANSFORM_TEX(i.uv,_Normalmap)));
        float3 normalWorld = normalize(mul(normalLocal.rgb,tangentTransform));
        //通过插值可以在面板中控制法线强度
        float3 finalNormal = lerp(worldNormal,normalWorld,_LocalNormalSild);

能量守恒理念在基础光照模型中的作用

能量守恒定律是自然界普遍的基本定律之一。一般表述为：能量既不会凭空产生，也不会凭空消失，它只会从一种形式转化为另一种形式，或者从一个物体转移到其它物体，而能量的总量保持不变。

将能量守恒定律应用到光照模型中:出射光线的能量永远不能超过入射光线的能量。可以用渲染方程来描述：

按照能量守恒的关系，首先计算镜面反射部分，它的值等于入射光线被反射的能量所占的百分比。然后漫反射部分就可以直接由镜面反射部分计算得出：

float kS = calculateSpecularComponent(...); // 镜面反射部分
float kD = 1.0 - ks;                        // 漫反射 部分

基础光照模型无法实现能量守恒，但是可以通过一些小trick来模拟能量守恒的效果：

• 通过对高光和漫反射光进行插值，达到高光部分既有镜面反射部分又有漫反射部分的效果
  specular = lerp(diffuse*specular,specular,_Gloss/255);
• 使用CubeMap来模拟间接光照的效果，使用TexCubeLod采样并通过控制CubeMap的mipmap等级和控制高光范围来实现控制表面粗糙度的效果
• float3 specular = _LightColor0.rgb * _Specular.rgb * pow(vDotr,_Gloss);
• float4 reflcol = texCUBElod(_Cubemap,float4(worldRef.rgb,(255-_Gloss)*8/(255)))*_EnvScale;
• 

基于能量守恒理念，自己写一套完整的光照模型，包含环境光照

仅参照先行版案例，在Blinn-Phong模型的基础上添加了几个trick和CubeMap环境光反射

高光范围调整

法线强度调整

环境光反射

片元着色代码：

fixed4 frag (v2f i) : SV_Target
            {
                fixed4 MainTex = tex2D(_MainTex, i.uv);
                //环境光
                float3 ambient = UNITY_LIGHTMODEL_AMBIENT.xyz * _Diffuse * MainTex.rgb;
                //归一化
                float3 worldLight = normalize(_WorldSpaceLightPos0.xyz);
                float3 worldNormal = normalize(i.worldNormal);

                //切线空间到世界空间转换矩阵
                i.normalDir = worldNormal;
                float3x3 tangentTransform = float3x3(i.tangentDir,i.bitangentDir,i.normalDir);

                //获取映射过的法线贴图,准备最终法线
                float3 normalLocal = UnpackNormal(tex2D(_Normalmap,TRANSFORM_TEX(i.uv,_Normalmap)));
                float3 normalWorld = normalize(mul(normalLocal.rgb,tangentTransform));
                float3 finalNormal = lerp(worldNormal,normalWorld,_LocalNormalSild);

                //Lambert
                float nDotl = max(0.0,dot(finalNormal,worldLight));
                //防止兰伯特的暗部纯黑，用环境光作为暗部，光照作为亮部，插值后得到diffuse
                //diffuse
                float3 diffuse = lerp(ambient.rgb * _Diffuse.rgb * MainTex.rgb , _LightColor0.rgb * _Diffuse.rgb * MainTex.rgb , nDotl);
                            
                //Blinn-Phong Model
                float3 viewDir = normalize(_WorldSpaceCameraPos.xyz - i.worldPos.xyz);
                float3 halfDir = normalize(worldLight + viewDir);
                float nDoth = saturate(dot(finalNormal,halfDir));

                //环境贴图
                float3 worldRef = normalize(reflect(-viewDir,worldNormal));
                float4 reflcol = texCUBElod(_Cubemap,float4(worldRef.rgb,(255-_Gloss)*8/(255)))*_EnvScale;
                
                float3 specular = _LightColor0.rgb * _Specular.rgb * pow(nDoth,_Gloss);
                //镜面反射与漫反射插值
                specular = lerp(diffuse*specular,specular,_Gloss/255);
                reflcol.rgb = lerp(reflcol * diffuse.rgb,reflcol,_Gloss/255);

                fixed3 color = diffuse + reflcol + specular;

                return fixed4(color,1.0);

                
            }

对比PBR模型的三要素:

1. 基于微平面的表面模型
2. 能量守恒
3. 基于物理的BRDF

这个光照模型只有1能实现，2通过模拟能达到类似的效果，3还没有实现。之后学习过PBR之后会回来进行优化（大概）